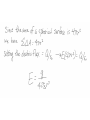* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ch. 18 sec.8,9 - Physics-YISS
Alternating current wikipedia , lookup
Superconductivity wikipedia , lookup
Hall effect wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Multiferroics wikipedia , lookup
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electrostatic generator wikipedia , lookup
Eddy current wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Electric machine wikipedia , lookup
Insulator (electricity) wikipedia , lookup
Skin effect wikipedia , lookup
History of electrochemistry wikipedia , lookup
Electroactive polymers wikipedia , lookup
Static electricity wikipedia , lookup
Lorentz force wikipedia , lookup
Electrocommunication wikipedia , lookup
Maxwell's equations wikipedia , lookup
Faraday paradox wikipedia , lookup
Electrical injury wikipedia , lookup
Electromotive force wikipedia , lookup
Electric charge wikipedia , lookup
Electromagnetic field wikipedia , lookup
Electric current wikipedia , lookup
18.8 THE ELECTRIC FIELD INSIDE A CONDUCTOR: SHIELDING • In conducting materials electric charges move in response to the forces that electric fields exert. • Ex. Suppose a piece of copper carriers a number of excess –e somewhere within it. • Each –e would experience a force of repulsion because of the electric field of its neighbors. • Since copper is a conductor the –e will move due to that force. • They rush to the surface of the copper, because coulomb’s law is affected by distance 1/r^2. • Once static equilibrium is established with all of the excess charge on the surface, no further movement of charge occurs. • Excess positive charge also moves to the surface of a conductor. • At equilibrium under electrostatic conditions, any excess charge resides on the surface of a conductor. • The interior of the copper is electrically neutral. • No net electric field because no net movement of free electrons. • A equilibrium under electrostatic conditions, the electric field is zero at any point within a conducting material. • Fig 18.30 • Uncharged, solid, cylindrical conductor at equilibrium in the central region of a parallel plate capacitor. • Induced charges on the surface of the cylinder alter the electric field lines of the capacitor. • An electric field cannot exist under these conditions, the electric field lines do not penetrate the cylinder. • They end or begin on the induced charges. • Test charge placed inside the conductor would feel no force due to the presence of the charges on the capacitor. • The conductor shields any charge within it from electric fields created outside the conductor. • The shielding results from the induced charges on the conductor surface. • Since the electric field is zero inside the conductor, nothing is disturbed if a cavity is cut from the interior of the material. • Stray electric fields are produced by hair dryers, blenders, vacuum cleaners. • These stray fields can interfere with the operation of sensitive electronic circuits; stereo amplifiers, tvs, and computers. • To eliminate such interference, circuits are often enclosed within metal boxes that provide shielding from external fields. • Fig. 18.30 • The electric field just outside the surface of a conductor is perpendicular to the surface at equilibrium under electrostatic conditions. 18.9 GAUSS’ LAW • Charge distribution: charges that are spread out over a region, rather than by a single point charge. • Gauss’ law describes the relationship between a charge distribution and the electric field it produces. • Carl Friedrich Gauss, German mathematician. • Electric flux: – Using both the idea of electric field and surface through which field passes. GAUSS’ LAW ON A POINT CHARGE • Assume point charge is positive. • Field line radiate outward in all directions. • E = kq/r^2, k can be expressed as k = 1/(4πεo), where εo is the permittivity of free space. • The equation is: • We place this point charge at the center of the imaginary spherical surface of radius r, called the Gaussian surface. • A = 4πr^2 so the equation can be written as EA = magnitude of E of the electric field at any point on the Gaussian surface and the area A of the surface. Electric flux = EA = ϕE permittivity is the measure of how much resistance is encountered when forming an electric field in a medium, permittivity relates to a material's ability to transmit (or "permit") an electric field. Problems take place in a vacuum, this is where this constant value comes from. • Form of Gauss’ law that applies to a point charge. • Electric flux depends only on the charge q within the Gaussian surface and is independent of the radius r of the surface. • • • • Using eq. 18.5 to use with arbitrary shapes. Fig. 18.34 Q = net charge Any arbitrary shape (doesn’t need to be spherical) • Must be closed • Divided the surface into many tiny sections with area ΔA1, ΔA2 and so on. Each section is so small that it is essentially flat and the electric field is a constant. • Electric field magnitude is EcosΦ • Φ is the angle between the electric field and the normal. • Electric flux through any one section is then (EcosΦ)ΔA • The Electric flux that passes through the entire Gaussian surface is the sum of all of these individual fluxes GAUSS’ LAW EXAMPLE 15: THE ELECTRIC FIELD OF A CHARGED THIN SPHERICAL SHELL EXAMPLE 16: THE ELECTRIC FIELD INSIDE A PARALLEL PLATE CAPACITOR Practice Questions 4. 5. 6. 7. 8.