* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Angles - Larose
Technical drawing wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
Toilet paper orientation wikipedia , lookup
Multilateration wikipedia , lookup
Line (geometry) wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Perceived visual angle wikipedia , lookup
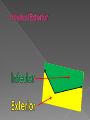
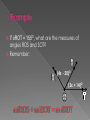
Angle › Formed by two rays with the same endpoint Vertex › The name for the common endpoint Sides › The rays that make up the angle An angle can be named in a few different ways: With an angle symbol and the vertex óA Or using three points The vertex must always be in the middle! › óBAC or › óCAB Or with a number on the inside of the angle › ó4 Interior contains all the points between the two sides Exterior contains all the points outside the angle Between 0 and 90 degrees xO Exactly 90O Between 90 and 180 degrees xO Exactly 180o xO Draw an angle on one side of paddy paper Fold the paper in half Trace the angle on the other side of the paper You should see two angles Answer Question 1 on the work sheet Cut out one of the angles leaving the other on the paper Cut the separate angle into two different angles through the vertex You should now have one angle on paper and one cut into two pieces Place the cut angle onto the original angle any way as long as the vertex lines up Answer question 2 Notice how the two pieces add up to the one angle Remember how two pieces of a line add up to the whole If point B is in the interior of óAOC, then óAOB + óBOC = óAOC If óROT = 155O, what are the measures of angles ROS and SOT? Remember: (4x - 20)O (3x + 14)O Plug in each piece and make it equal the total (4x - 20)O (3x + 14)O Combine like terms Add 6 to both sides Divide by 7 If óROT = 155O, what are the measures of angles ROS and SOT? So if x = 23, plug it into 4x – 20 to find óROS (4x - 20)O (3x + 14)O If óROT = 155O, what are the measures of angles ROS and SOT? So if x = 23, plug it into 3x + 14 to find óSOT 72O (3x + 14)O If óROT = 155O, what are the measures of angles ROS and SOT? Do your answers make sense? 72O 83O Two or more angles that have the same measure Take one piece of Patty Paper (tracing paper) Draw two straight and intersecting lines The angles don’t matter except they should not be 90 degrees Label the intersection point E Put a point on each ray A, B, C, and D Fold the paper at the point E so that ray EA and ray ED line up on top of each other Answer questions 1 and 2 Fold the paper at the point E so that ray EA and ray EB line up on top of each other Answer questions 3 and 4 Mark the pairs of congruent angles Notice how the vertical angles (across from each other) are congruent Two angles whose sides are opposite rays Two coplanar angles with a common side, a common vertex, and no common interior points Two angles whose measures have a sum of 90 degrees. Each angle is called the complement of the other Two angles whose measures have a sum of 180 degrees Each angle is called the supplement of each other If two angles form a linear pair, then they are supplementary