Download isosceles triangles

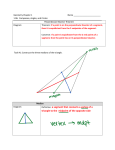
In a scalene triangle, all sides and internal angles are different from one
other.
In isosceles triangles, two sides are equal in length.
An isosceles triangle also has two equal angles:
the angles opposite the two equal sides.
In geometry, the centroid, geometric center, or barycenter of a plane
figure is the intersection of all straight lines that divide the figure into
two parts of equal moment about the line.
Definition:
The circocentre of a
triangle is the meeting
point of three axes.
To build the circocentre of any triangle ABC, we draw the axes of at least
two sides of the triangle.
Please remember that the axis of a segment is the locus of points
equidistant from the extremes of the segment. The axis of a segment
passing through the midpoint and is perpendicular to the segment.
Definition:
orthocentre of a triangle
is the meeting point of
three heights
To build the orthocentre of any triangle ABC, we draw the heights of
at least two sides of the triangle.
Please remember that the height on one side of the triangle is the
perpendicular segment from the top led to the opposite side.
Definition:
the concentration of a
triangle is the meeting
point of the three
bisectors.
To construct the concentration of any triangle ABC, we draw the bisector
of at least two corners of the triangle.
Please remember that the bisector of an angle is the locus of the points in
the plane equidistant from the sides of the angle. This is reflected in the
fact that the bisector of an angle is a ray that divides the angle into two
equal parts.