* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 11
Buck converter wikipedia , lookup
Fault tolerance wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Opto-isolator wikipedia , lookup
Power engineering wikipedia , lookup
Power inverter wikipedia , lookup
Electronic music wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Electrical ballast wikipedia , lookup
Three-phase electric power wikipedia , lookup
Public address system wikipedia , lookup
Ground (electricity) wikipedia , lookup
Electronic musical instrument wikipedia , lookup
Electrician wikipedia , lookup
Voltage optimisation wikipedia , lookup
Power electronics wikipedia , lookup
Electronic paper wikipedia , lookup
History of electric power transmission wikipedia , lookup
Oscilloscope history wikipedia , lookup
Stray voltage wikipedia , lookup
Electrical engineering wikipedia , lookup
Alternating current wikipedia , lookup
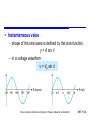
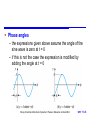
Measurement of Voltages and Currents Chapter 11 Introduction Sine waves Square waves Measuring Voltages and Currents Analogue Ammeters and Voltmeters Digital Multimeters Oscilloscopes Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Introduction 11.1 Alternating currents and voltages vary with time and periodically change their direction Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Sine Waves 11.2 Sine waves – by far the most important form of alternating quantity important properties are shown below Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Instantaneous value – shape of the sine wave is defined by the sine function y = A sin – in a voltage waveform v = Vp sin Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Angular frequency – frequency f (in hertz) is a measure of the number of cycles per second – each cycle consists of 2 radians – therefore there will be 2f radians per second – this is the angular frequency (units are rad/s) = 2f Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Equation of a sine wave – the angular frequency can be thought of as the rate at which the angle of the sine wave changes – at any time = t – therefore v = Vp sin t or v = Vp sin 2ft or i = Ip sin 2ft – similarly i = Ip sin t Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Example – see Example 11.2 in the course text Determine the equation of the following voltage signal. From diagram: Period is 50 ms = 0.05 s Thus f = 1/T =1/0.05 = 20 Hz Peak voltage is 10 V Therefore v Vp sin 2ft 10 sin 2 20t 10 sin 126 t Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Phase angles – the expressions given above assume the angle of the sine wave is zero at t = 0 – if this is not the case the expression is modified by adding the angle at t = 0 Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Phase difference – two waveforms of the same frequency may have a constant phase difference we say that one is phase-shifted with respect to the other Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Average value of a sine wave – average value over one (or more) cycles is clearly zero – however, it is often useful to know the average magnitude of the waveform independent of its polarity we can think of this as the average value over half a cycle… … or as the average value of the rectified signal Vav 1 0Vp sin dθ Vp 2Vp cos 0 0.637 Vp Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Average value of a sine wave Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› r.m.s. value of a sine wave – the instantaneous power (p) in a resistor is given by p v2 R – therefore the average power is given by Pav [ average (or mean) of v 2 ] R v2 R – where v 2 is the mean-square voltage Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› While the mean-square voltage is useful, more often we use the square root of this quantity, namely the root-mean-square voltage Vrms – where Vrms = v2 – we can also define Irms = i2 – it is relatively easy to show that (see text for analysis) Vrms 1 V 0.707 Vp p 2 Irms 1 I 0.707 I p 2 p Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› r.m.s. values are useful because their relationship to average power is similar to the corresponding DC values P av V rms rms P I av 2 V P av I rms R 2 rms R Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Form factor – for any waveform the form factor is defined as Form factor r.m.s. value average value – for a sine wave this gives Form factor 0.707 V 0.637 V p 1.11 p Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Peak factor – for any waveform the peak factor is defined as Peak factor peak value r.m.s. value – for a sine wave this gives V p Peak factor 1.414 0.707 V p Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Square Waves 11.3 Frequency, period, peak value and peak-to-peak value have the same meaning for all repetitive waveforms Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Phase angle – we can divide the period into 360 or 2 radians – useful in defining phase relationship between signals – in the waveforms shown here, B lags A by 90 – we could alternatively give the time delay of one with respect to the other Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Average and r.m.s. values – the average value of a symmetrical waveform is its average value over the positive half-cycle – thus the average value of a symmetrical square wave is equal to its peak value V V av p – similarly, since the instantaneous value of a square wave is either its peak positive or peak negative value, the square of this is the peak value squared, and V V rms p Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Form factor and peak factor – from the earlier definitions, for a square wave V p Form factor r.m.s. value 1 .0 average value V p Peak factor V p peak value 1 .0 r.m.s. value V p Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring Voltages and Currents 11.4 Measuring voltage and current in a circuit – when measuring voltage we connect across the component – when measuring current we connect in series with the component Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring Voltages and Currents 11.4 Loading effects – voltage measurement – our measuring instrument will have an effective resistance (RM) – when measuring voltage we connect a resistance in parallel with the component concerned which changes the resistance in the circuit and therefore changes the voltage we are trying to measure – this effect is known as loading Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring Voltages and Currents 11.4 Loading effects – current measurement – our measuring instrument will have an effective resistance (RM) – when measuring current we connect a resistance in series with the component concerned which again changes the resistance in the circuit and therefore changes the current we are trying to measure – this is again a loading effect Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Analogue Ammeters and Voltmeters 11.5 Most modern analogue ammeters are based on moving-coil meters – see Chapter 4 of textbook Meters are characterised by their full-scale deflection (f.s.d.) and their effective resistance (RM) – typical meters produce a f.s.d. for a current of 50 A – 1 mA – typical meters have an RM between a few ohms and a few kilohms Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring direct currents using a moving coil meter – use a shunt resistor to adjust sensitivity – see Example 11.5 in set text for numerical calculations Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring direct voltages using a moving coil meter – use a series resistor to adjust sensitivity – see Example 11.6 in set text for numerical calculations Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measuring alternating quantities – moving coil meters respond to both positive and negative voltages, each producing deflections in opposite directions – a symmetrical alternating waveform will produce zero deflection (the mean value of the waveform) – therefore we use a rectifier to produce a unidirectional signal – meter then displays the average value of the waveform – meters are often calibrated to directly display r.m.s. of sine waves all readings are multiplied by 1.11 – the form factor for a sine wave – as a result waveforms of other forms will give incorrect readings for example when measuring a square wave (for which the form factor is 1.0, the meter will read 11% too high) Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Analogue multimeters – general purpose instruments use a combination of switches and resistors to give a number of voltage and current ranges – a rectifier allows the measurement of AC voltage and currents – additional circuitry permits resistance measurement – very versatile but relatively low input resistance on voltage ranges produces considerable loading in some situations A typical analogue multimeter Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Digital Multimeters 11.6 Digital multimeters (DMMs) are often (inaccurately) referred to as digital voltmeters or DVMs – at their heart is an analogue-to-digital converter (ADC) A simplified block diagram Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measurement of voltage, current and resistance is achieved using appropriate circuits to produce a voltage proportional to the quantity to be measured – in simple DMMs alternating signals are rectified as in analogue multimeters to give its average value which is multiplied by 1.11 to directly display the r.m.s. value of sine waves – more sophisticated devices use a true r.m.s. converter which accurately produced a voltage proportional to the r.m.s. value of an input waveform A typical digital multimeter Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Oscilloscopes 11.7 An oscilloscope displays voltage waveforms A simplified block diagram Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› A typical analogue oscilloscope Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Measurement of phase difference Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#› Key Points The magnitude of an alternating waveform can be described by its peak, peak-to-peak, average or r.m.s. value The root-mean-square value of a waveform is the value that will produce the same power as an equivalent direct quantity Simple analogue ammeter and voltmeters are based on moving coil meters Digital multimeters are easy to use and offer high accuracy Oscilloscopes display the waveform of a signal and allow quantities such as phase to be measured. Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 11.‹#›