Download Chapter 11

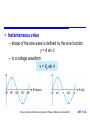
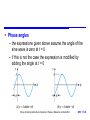
Measurement of Voltages and Currents Chapter 11
 Introduction
 Sine waves
 Square waves
 Measuring Voltages and Currents
 Analogue Ammeters and Voltmeters
 Digital Multimeters
 Oscilloscopes
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Introduction
11.1
 Alternating currents and voltages vary with time and
periodically change their direction
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Sine Waves
11.2
 Sine waves
– by far the most important form of alternating quantity
 important properties are shown below
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Instantaneous value
– shape of the sine wave is defined by the sine function
y = A sin 
– in a voltage waveform
v = Vp sin 
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Angular frequency
– frequency f (in hertz) is a measure of the number of
cycles per second
– each cycle consists of 2 radians
– therefore there will be 2f radians per second
– this is the angular frequency  (units are rad/s)
 = 2f
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Equation of a sine wave
– the angular frequency  can be thought of as the rate
at which the angle of the sine wave changes
– at any time
 = t
– therefore
v = Vp sin t
or
v = Vp sin 2ft
or
i = Ip sin 2ft
– similarly
i = Ip sin t
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Example – see Example 11.2 in the course text
Determine the equation of the following voltage signal.
From diagram:
 Period is 50 ms = 0.05 s
 Thus f = 1/T =1/0.05 = 20 Hz
 Peak voltage is 10 V
 Therefore
v  Vp sin 2ft
 10 sin 2 20t
 10 sin 126 t
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Phase angles
– the expressions given above assume the angle of the
sine wave is zero at t = 0
– if this is not the case the expression is modified by
adding the angle at t = 0
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Phase difference
– two waveforms of the same frequency may have a
constant phase difference
 we say that one is phase-shifted with respect to the other
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Average value of a sine wave
– average value over one (or more) cycles is clearly zero
– however, it is often useful to know the average
magnitude of the waveform independent of its polarity
 we can think of this as
the average value over
half a cycle…
 … or as the average value
of the rectified signal
Vav 
1


0Vp sin dθ

Vp

2Vp


 cos 0
 0.637  Vp
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Average value of a sine wave
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 r.m.s. value of a sine wave
– the instantaneous power (p) in a resistor is given by
p 
v2
R
– therefore the average power is given by
Pav 
[ average (or mean) of v 2 ]
R

v2
R
– where v 2 is the mean-square voltage
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 While the mean-square voltage is useful, more often
we use the square root of this quantity, namely the
root-mean-square voltage Vrms
– where Vrms =
v2
– we can also define Irms =
i2
– it is relatively easy to show that (see text for analysis)
Vrms  1  V  0.707  Vp
p
2
Irms  1  I  0.707  I p
2 p
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 r.m.s. values are useful because their relationship to
average power is similar to the corresponding DC
values
P
av
V
rms rms

P
I
av
2
V
P
av
I
rms
R
2
rms
R
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Form factor
– for any waveform the form factor is defined as
Form factor  r.m.s. value
average value
– for a sine wave this gives
Form factor 
0.707 V
0.637 V
p
 1.11
p
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Peak factor
– for any waveform the peak factor is defined as
Peak factor 
peak value
r.m.s. value
– for a sine wave this gives
V
p
Peak factor 
 1.414
0.707 V
p
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Square Waves
11.3
 Frequency, period, peak value and peak-to-peak
value have the same meaning for all repetitive
waveforms
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Phase angle
– we can divide the period
into 360 or 2 radians
– useful in defining phase
relationship between signals
– in the waveforms shown
here, B lags A by 90
– we could alternatively give
the time delay of one with
respect to the other
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Average and r.m.s. values
– the average value of a symmetrical waveform is its
average value over the positive half-cycle
– thus the average value of a symmetrical square wave
is equal to its peak value
V V
av
p
– similarly, since the instantaneous value of a square
wave is either its peak positive or peak negative value,
the square of this is the peak value squared, and
V
V
rms
p
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Form factor and peak factor
– from the earlier definitions, for a square wave
V
p
Form factor  r.m.s. value 
 1 .0
average value V
p
Peak factor 
V
p
peak value

 1 .0
r.m.s. value V
p
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Measuring Voltages and Currents
11.4
 Measuring voltage and current in a circuit
– when measuring voltage we connect across the component
– when measuring current we connect in series with the component
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Measuring Voltages and Currents
11.4
 Loading effects – voltage
measurement
– our measuring instrument will
have an effective resistance (RM)
– when measuring voltage we
connect a resistance in parallel
with the component concerned
which changes the resistance in
the circuit and therefore changes
the voltage we are trying to
measure
– this effect is known as loading
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Measuring Voltages and Currents
11.4
 Loading effects – current
measurement
– our measuring instrument will have an
effective resistance (RM)
– when measuring current we connect a
resistance in series with the component
concerned which again changes the
resistance in the circuit and therefore
changes the current we are trying to
measure
– this is again a loading effect
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Analogue Ammeters and Voltmeters
11.5
 Most modern analogue
ammeters are based on
moving-coil meters
– see Chapter 4 of textbook
 Meters are characterised by their full-scale deflection (f.s.d.)
and their effective resistance (RM)
– typical meters produce a f.s.d. for a current of 50 A – 1 mA
– typical meters have an RM between a few ohms and a few kilohms
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Measuring direct
currents using a
moving coil meter
– use a shunt resistor
to adjust sensitivity
– see Example 11.5 in
set text for numerical
calculations
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Measuring direct
voltages using a
moving coil meter
– use a series resistor
to adjust sensitivity
– see Example 11.6 in
set text for numerical
calculations
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Measuring alternating quantities
– moving coil meters respond to both positive and negative
voltages, each producing deflections in opposite directions
– a symmetrical alternating waveform will produce zero deflection
(the mean value of the waveform)
– therefore we use a rectifier to produce a unidirectional signal
– meter then displays the average value of the waveform
– meters are often calibrated to directly display r.m.s. of sine waves
 all readings are multiplied by 1.11 – the form factor for a sine wave
– as a result waveforms of other forms will give incorrect readings
 for example when measuring a square wave (for which the form
factor is 1.0, the meter will read 11% too high)
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Analogue multimeters
– general purpose instruments use a
combination of switches and resistors
to give a number of voltage and
current ranges
– a rectifier allows the measurement of
AC voltage and currents
– additional circuitry permits resistance
measurement
– very versatile but relatively low input
resistance on voltage ranges
produces considerable loading in
some situations
A typical analogue multimeter
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Digital Multimeters
11.6
 Digital multimeters (DMMs) are often (inaccurately)
referred to as digital voltmeters or DVMs
– at their heart is an analogue-to-digital converter (ADC)
A simplified block diagram
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Measurement of voltage, current and
resistance is achieved using appropriate
circuits to produce a voltage proportional
to the quantity to be measured
– in simple DMMs alternating signals are
rectified as in analogue multimeters to
give its average value which is multiplied
by 1.11 to directly display the r.m.s. value
of sine waves
– more sophisticated devices use a true
r.m.s. converter which accurately
produced a voltage proportional to the
r.m.s. value of an input waveform
A typical digital multimeter
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Oscilloscopes
11.7
 An oscilloscope displays voltage waveforms
A simplified block diagram
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 A typical analogue oscilloscope
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
 Measurement of phase difference
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›
Key Points
 The magnitude of an alternating waveform can be
described by its peak, peak-to-peak, average or r.m.s.
value
 The root-mean-square value of a waveform is the value
that will produce the same power as an equivalent direct
quantity
 Simple analogue ammeter and voltmeters are based on
moving coil meters
 Digital multimeters are easy to use and offer high accuracy
 Oscilloscopes display the waveform of a signal and allow
quantities such as phase to be measured.
Storey: Electrical & Electronic Systems © Pearson Education Limited 2004
OHT 11.‹#›