Download Section 10.6 Radical Equations

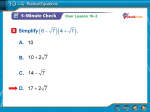
Math 123 - Section 10.6 - Radical Equations - Page 1
Section 10.6
Radical Equations
I.
Procedure - Square Root Equations
A.
Use the Addition Property and Multiplication Property to isolate the radical sign.
B.
Square both sides.
C.
Solve the result.
D.
Check for any extraneous solutions answers that when substituted back into the
original equation will give us a false statement or will cause us to take the square
root of a negative number.
x means the positive square root of x.
E.
Don’t forget that the symbol
F.
Examples – Solve each Square Root Equation.
1.
6x + 1 − x = −1
We first have to isolate the radical by adding x to both sides to get:
6x + 1 = x − 1
2
We now can square both sides. Remember that (x – 1) = (x – 1)(x – 1).
Also, squaring a radical gets rid of the radical sign and leaves the radicand
alone.
2
6x + 1 = x – 2x + 1
This is a quadratic, so we need to get it into standard form (= 0), so subtract
6x from both sides and subtract 1 from both sides to get:
2
0 = x – 8x
Factor out the GCF to get:
0 = x(x – 8)
Use the Zero Product Property to solve for x:
x = 0 OR x – 8 = 0
x = 0 OR x = 8
We now need to check for extraneous solutions:
First we check x = 0.
6(0) + 1 − 0 = 0 + 1 − 0 = 1 ≠ −1
So x = 0 is an extraneous solution and we throw it out.
Now let’s check x = 8:
6(8) + 1 − 8 = 48 + 1 − 8 = 49 − 8 = 7 − 8 = −1
Answer: x = 8
2.
6x − 8 − 1 = 3
First, we isolate the radical by adding 1 to both sides to get:
6x − 8 = 4
Now we square both sides to get:
6x – 8 = 16
To solve this (since it’s not a quadratic), we will first add 8 to both sides to get:
6x = 24
Now divide both sides by 6 to get:
x=4
Now we check for extraneous solutions:
6(4) − 8 − 1 = 24 − 8 − 1 = 16 − 1 = 4 − 1 = 3
Answer: x = 4
© Copyright 2009 by John Fetcho. All rights reserved
Math 123 - Section 10.6 - Radical Equations - Page 2
3.
Now you try one: 2 x = 12
Answer: x = 36
4.
x + 10 = −3
We see that the left side is the POSITIVE square root of x + 10, while the right
side is negative. Can a positive number ever be equal to a negative number?
Answer: ∅
5.
5x − 3x + 6 = 0
The first thing that we need to do is get one radical per side in this equation.
So we get:
5x = 3x + 6
Now we can square both sides to get:
5x = 3x + 6
Subtracting 3x from both sides we get:
2x = 6
Dividing both sides by 2, we get:
x=3
Checking for extraneous solutions, we get:
5(3) − 3(3) + 6 = 15 − 9 + 6 = 15 − 15 = 0
Answer: x = 3
6.
Now you try one:
6x − 2x + 8 = 0
Answer: x = 2
III.
Procedure - Cube Root Equations
A.
Use the Addition Property and Multiplication Property to isolate the radical sign.
B.
Cube both sides.
C.
Solve the result.
D.
Check for any extraneous solutions answers that when substituted back into the
original equation will give us a false statement.
E.
Examples – Solve each Cube Root Equation.
3
1.
4x − 3 − 5 = 0
The first step is to add 5 to both sides to isolate the radical.
3
4x − 3 = 5
Cube both sides to clear the radical.
(
3
4x − 3
)
3
= (5 )
3
4x − 3 = 125
Add 3 to both sides to isolate the variable term.
4x = 128
Divide both sides by 4 to isolate the variable.
x = 32
Check for extraneous solutions.
3 4(32) − 3 − 5 = 0
128 − 3 − 5 = 0
125 − 5 = 0
5−5=0
3
3
Answer:
x = 32
© Copyright 2009 by John Fetcho. All rights reserved
Math 123 - Section 10.6 - Radical Equations - Page 3
2.
Now you try one:
Answer:
3
2 x + 11 = 3
x=8
© Copyright 2009 by John Fetcho. All rights reserved