Download Solving Radical Equations in One Variable Algebraically Principle of

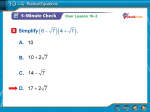
Solving Radical Equations in One
Variable Algebraically
Solve square-root equations in one variable algebraically
Solve radical equations in one variable algebraically
Solve equations containing variable expressions with
rational exponents algebraically
Principle of Powers
Steps to Solve a Radical Equation
1.
2.
3.
4.
Isolate the radical. If the equation has more
than one radical, choose one of the radicals
to isolate.
Raise each side of the equation to a power
equal to the index of the radical.
Solve the resulting equation. If the equation
still has a radical, repeats steps 1 and 2.
Check the potential solutions in the original
equation.
1
Solve Algebraically
x = −5
( x)
2
= (− 5)
2
x = 25
25 = − 5
5 ≠ −5
∅
Extraneous Solutions
Solving Radical Equations
x + 3 − 7 = −3
Solution
(
Check
x + 3 − 7 = −3
13 + 3 − 7 = −3
x+3 = 4
16 − 7 = −3
4 − 7 = −3
− 3 = −3
)
x + 3 = (4 )
2
x + 3 = 16
x = 13
2
Solution Checks
2
Solving Radical Equations
3
3x + 1 = 5
Solution
3
(
3
Check
3x + 1 = 5
)
3
3( 124
) +1 = 5
3
3
3 x + 1 = (5)
3
3
3 x + 1 = 125
125 = 5
3 x = 124
124
3
x=
Solution Checks
Solving Radical Equations
2x − 4 = 3 1 − 8x
3
Solution
3
(
3
Check
2x − 4 = 1 − 8x
3
) ( 1 − 8x )
3
2x − 4 =
3
3
2x − 4 = 1− 8x
2
1
1
− 4 = 3 1− 8
2
2
3
3
10 x = 5
x=
3
1− 4 = 3 1− 4
−3 = 3 −3
Solution Checks
1
2
Example
2/3
Solve (2 y − 3) = 4
2y = 3±8
Solution
(2 y − 3)
2/3
[(2 y − 3) ]
2 /3 3/ 2
[(2 y − 3) ]
[(2 y − 3) ]
2 y − 3 = ±8
=4
= ±[4]
y=
3/ 2
2 / 3 3/ 2
= ± 43
2/3 3/ 2
= ± 64
y=
3±8
2
11 − 5
or
2
2
Solutions Check
The ± is needed because your
are taking the square root.
3
Example
Solve
a 2 + 2a + 1 = a + 5
− 24 = 8a
a = −3
Solution
(a
a 2 + 2a + 1 = a + 5
2
)
2
+ 2a + 1 = (a + 5)
2
a + 2a + 1 = a + 10a + 25
2a + 1 = 10a + 25
2
2
Solution Checks
4