Download Theorems - MOC-FV

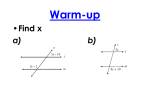
Bell Ringer
Complete
Binder Check #1
Unit 4 Lesson 2
Quiz
Review for Unit 4
Lesson 1 & 2 TEST
• Practice Set #4
• 6 minutes
• Discuss Results
• TOMORROW
y  x 1
Sketch a graph the
y  x2
functions:
Using the right triangle , find the sine of the
smallest angle.
50
40
30
Linear Pair:
• A pair of adjacent angles that are formed when 2 lines intersect…total 180
Postulates:
• Basic math facts that are accepted as true w/o proof
Theorems:
• Mathematical statements /facts that are proven using deductive reasoning
Perpendicular Lines:
Supplementary
Angles:
Parallel Lines:
Transversal:
• 2 lines that intersect to form a right angle (90)
• We proved they form 4 right angles
• Perpendicular symbol: 
• 2 angles whose sum is 180
• Lines in the same plane that do not intersect
• Parallel symbol: ||
• A line that intersects 2 parallel lines
Linear
Pair
Postulate:
• If two angles are a linear
pair, then the sum of
their measures is 180
(LPP)
Vertical
Angles
Theorem
(VAT)
• Vertical angles are
congruent
• Occur whenever 2 lines
intersect
Corresponding
Angle
Assumption
(CAA)
4 Parallel Line
Theorems:
• If 2 parallel lines are cut by a transversal, then corresponding
angles are congruent
•
•
•
•
•If 2 parallel lines are cut by a transversal then:
a) Alternate interior angles are congruent (AIA Thm)
b) Alternate exterior angles are congruent (AEA Thm)
c) Same side interior angles are supplementary (SSIA Thm)
d) Same side exterior angles are supplementary (SSEA Thm)
Parallel
Lines
Postulate
(PLP)
• 2 lines cut by a transversal are parallel if and only if corresponding
angles are congruent
• This is a two fold postulate:
• If 2 parallel lines are cut by a transversal then corresponding
angles are congruent (also known as CAA)
• AND
• If corresponding angles on 2 lines cut by a transversal are
congruent then the lines are parallel
Angle
Theorems to
Prove that
Lines are
Parallel
•
•
•
•
•
•If :
a) Alternate interior angles are congruent
b) Alternate exterior angles are congruent
c) Same side interior angles are supplementary
d) Same side exterior angles are supplementary
THEN:
the lines are parallel.
Triangle
Angle Sum
Theorem
•The sum of the 3 interior angles of a triangle is 180
(TAST)
Angle
Addition
Postulate
(AAP)
• Formal definition: If P is a point in the interior of <ABC,
then m<ABP + m<PBC = m<ABC
A
B
P
C
• Smaller adjacent angles can be added together to equal
larger angle
Exterior
Angle
Theorem of
Triangles
(EATT)
• The exterior angle of a triangle is equal
to the sum of the 2 remote interior angles
Remote interior
angles
Exterior angle
Properties of
Equality
Transitive POE
• Substitution
• Addition, Subtraction, Multiplication, and Division
• If a = b and b = c, then a = c
• Similar to the Substitution POE
Triangle Congruency
Theorems:
• SSS, SAS, ASA, AAS, HL
Reflexive Property of
Equality
• Anything is equal to itself
CPCTC
• Corresponding Parts of Congruent Triangles are
Congruent
• All radii of the
same circle are
congruent
Circle
Concepts • Congruent
circles have
congruent radii
An angle is a right angle if and only if it has a measure of 90 degrees:
Write as 2 separate if then statements:
If the critter is a frog, then it is green.
Riley's pet Kermit is a frog... what if anything can you conclude?
Suzi's pet is green...what if anything can you conclude?
If you are 16 yrs old then you are eligible to apply for a license.
Write the converse of this statement?
Conjecture: If you add 2 odd whole numbers then the sum is always even.
Prove or disprove
Conjecture: If you multiply 2 odd integers the product is always odd
Prove or disprove
Conjecture: The sum of 3 consecutive whole numbers is always divisible by 3
Prove or disprove:
Conjecture: The product of an even and an odd integer is always odd
Prove or disprove:
1