Download predicate

Predicate Calculus
Formal Methods in Verification of
Computer Systems
Jeremy Johnson
Outline
1. Motivation
1. Variables, quantifiers and predicates
2. Syntax
1. Terms and formulas
2. Quantifiers, scope and substitution
3. Rules of natural deduction for quantifiers
4. Semantics
1. Models and semantic entailment
5. Undecidability and limitations
Example 1
• Every student is younger than some
instructor
• x ( S(x)  y(I(y)  Y(x,y) )
• S(x) : x is a student
• I(x) : is an instructor
• Y(x,y) : x is younger than y
Example 2
• Not all birds can fly
•  x ( B(x)  F(x) )
• x ( (B(x)   F(x) )
• B(x) : x is a bird
• F(x) : x can fly
• Semantically equivalent formulas
Example 3
• Every child is younger than its mother
• x y ( C(x)  M(y,x)  Y(x,y) )
• C(x) : x is child
• M(x,y) : x is y’s mother
• Y(x,y) : x is younger than y
• x ( C(x)  Y(x,m(x))
• m(x) : function for mother of x
Example 4
• Andy and Paul have the same maternal
grandmother
• x y u v ( M(x,y)  M(y,a)  M(u,v) 
M(v,p)  x = u )
• m(m(a)) = m(m(p))
• a, b : variables for Andy and Paul
• = : binary predicate
Example 5
• Everyone has a mother
• x y ( M(y,x) )
• x y ( M(y,x) ) [ not equivalent ]
• Everyone has exactly one mother
• x y ( M(y,x)  z (M(z,x)  z = y )
Example 6
• Some people have more than one brother
• x y1 y2 ( B(y1,x)  B(y2,x)  (y1 = y2)
)
Comparison to Propositional
Calculus
• Proof calculus for predicate calculus
• 1,…,n ⊢  [ extend natural deduction ]
• Provide semantics for predicate calculus
• 1,…,n ⊨  [ models needed to evaluate
functions and predicates – may not be finite ]
• Soundness and Completeness
• 1,…,n ⊨  holds iff 1,…,n ⊢  is valid
• Undecidable
• No program exists that can always determine
if ⊨  holds
Terms
• Terms are made up of variables, constants,
and functions
• Term ::=
• Variable
• If c is a nullary function c is a term
• If t1,…,tn are terms and f is an n-ary function
then f(t1,…,tn ) is a term
Formulas
• Formula ::=
• P is a predicate and t1,…,tn are terms then
P(t1,…,tn) is a formula
• If  is a formula  is a formula
• If 1 and 2 are formulas, 1  2, 1  2, 1
 2 are formulas
• If  is a formula and x is a variable x  and
x  are formulas
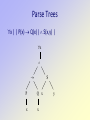
Parse Trees
x ( ( P(x)  Q(x) )  S(x,y) )
x


S
P
Q x
x
x
y
Free and Bound Variables
• An occurrence of x in  is free if it is a leaf
node in the parse tree for  with no
quantifier as an ancestor

x



S
P
Q x
x
x

x
y

Q
y
P
Q
P
x
x
x
Substitution
• Given a variable x, a term t and a formula
, [t/x] is the formula obtained by
replacing each free occurrence of x by t



x

[f(x,y)/x]

Q
y
P
Q
P
x
x
x

x


Q
y
P
Q
P
x
x
f
x y
Variable Capture
• t is free for x in  if
no free x occurs in
 in the scope of
any quantifier for
any variable y
occurring in t.

S
y
x

P
Q
x
y
Variable Capture
• t is free for x in  if
no free x occurs in
 in the scope of
any quantifier for
any variable y
occurring in t.

S
y
x

P
Q
f
y
y y
Equality Rules
• Introduction Rule
=i
t=t
• Elimination Rule
t1 = t2 [t1/x]
[t2/x]
=e
Equivalence Relation
• Symmetry: 𝑡1 = 𝑡2 ⊢ 𝑡2 = 𝑡1
1
𝑡1 = 𝑡2
premise
2
𝑡1 = 𝑡1
=i
3
𝑡2 = 𝑡1
=e 1,2
• Transitivity: 𝑡1 = 𝑡2, 𝑡2 = 𝑡3 ⊢ 𝑡1 = 𝑡3
1
𝑡1 = 𝑡2
premise
2
𝑡2 = 𝑡3
premise
3
𝑡1 = 𝑡3
=e 2,1
Conjunction Rules
• Introduction Rule
 

i
• Elimination Rule


 e1


 e2
Universal Quantification Rules
• Introduction Rule
x0
…
[x0/x]
x 
x i
• Elimination Rule
x 
[t/x]
x e
Illegal Substitution Leads to
False Reasoning
x 
 = y (x < y)
[y/x] = y (y < y)
y is not free for x in 
Example Proof
• 𝑥 P 𝑥  Q 𝑥 , 𝑥P(𝑥) ⊢ 𝑥Q(𝑥)
1
𝑥 P 𝑥  Q 𝑥 ,
premise
2
𝑥𝑃(𝑥)
premise
3
x0
P(x0) Q(x0)
𝑥 e1
4
P(x0)
𝑥 e2
5
Q(x0)
e3,4
6
𝑥 Q(𝑥)
𝑥 𝑖3 − 5
Disjunction Rules
• Introduction Rule



 i1

 i2
• Elimination Rule (proof by case analysis)

…
 


…

e
Existential Quantification Rules
• Introduction Rule
[t/x]
x 
x i
• Elimination Rule (proof by case analysis)
x 
x0 [x0/x]
…


e
Example Proof
• 𝑥 Q 𝑥  R 𝑥 , 𝑥(P 𝑥 Q(𝑥)) ⊢
𝑥(P 𝑥 R(𝑥))
1
𝑥 Q 𝑥  R 𝑥 ,
premise
2
𝑥(P 𝑥 Q(𝑥))
premise
3
x0
P(x0)  Q(x0)
assumption
4
Q 𝑥0  R 𝑥0
𝑥 e1
5
Q(x0)
e2 3
6
R 𝑥0
 𝑒 4,5
7
P(x0)
e1 3
8
P(x0)  R(x0)
i7,6
9
𝑥(P 𝑥 R(𝑥))
𝑥i 8
10
𝑥(P 𝑥 R(𝑥))
𝑥e 2,3-9
Quantifier Equivalences
1. x  ⊣⊢ x  
2.   x  ⊣⊢ x  
3. x    ⊣⊢ x (  ) [x not free in ]
4. x    ⊣⊢ x (  )
5.  x    ⊣⊢  x (  )
6.  x    ⊣⊢  x (  )
7. x (  ) ⊣⊢   x 
8.  x (  ) ⊣⊢ x   
9. x (  ) ⊣⊢  x   
10. x (  ) ⊣⊢    x 
Quantifier Equivalences
1.
2.
3.
4.
x   x  ⊣⊢ x (  )
 x    x  ⊣⊢ x (  )
x y  ⊣⊢ y x 
 x  y  ⊣⊢  y  x 
De Morgan’s Law
(p1 𝑝2) ⊢ ( p1𝑝2)
1
(p1 𝑝2)
premise
2
( p1𝑝2)
assumption
3
 p1
assumption
4
 p1𝑝2
i1 3
5
⊥
e4,2
6
p1
PBC 3-5
7
 p2
assumption
8
 p1𝑝2
i2 7
9
⊥
e4,2
10
p2
PBC 7-9
11
(p1 𝑝2)
i 6,1-
12
⊥
e 11,1
13
( p1𝑝2)
PBC 2-12
Generalized De Morgan’s Law
x P(x) ⊢ x P(x)
1
x P(x)
premise
2
x P(x)
assumption
4
P(x0)
assumption
5
x P(x)
x i 4
6
⊥
e 5,2
7
P(x0)
PBC 4-6
8
x P(x)
x i 3-7
9
⊥
e 8,1
10
x P(x)
PBC 2-9
3
x0
Generalized De Morgan’s Law
x  ⊢ x 
1
x
premise
2
x 
assumption
4
[x0/x]
assumption
5
x 
x I 4
6
⊥
e 5,2
7
[x0/x]
PBC 4-6
8
x 
x i 3-7
9
⊥
e 8,1
10
x 
PBC 2-9
3
x0
Exercise
Prove the reverse x  ⊢ x 
Models
• Let F be a set of functions and P a set of
predicates. A model M for (F,P) consists of
• A non-empty set A [universe] of concrete
values
• For each nullary f  F an element of A = fM
• For each n-ary f  F a function fM : An  A
• For each n-ary P  P a subset PM  An
Example 1
• F = {i} and P = {R,F}
• i a constant function, R binary and F unary
predicates
• Model – A set of states, initial state i, state
transitions R, final states F
• A = {a,b,c}
• iM = a
• RM = {(a,a),(a,b),(a,c),(b,c), (c,c)}
• FM = {b,c}
Example 1
• y R(i,y)
• F(i)
• x y z (R(x,y)  R(x,z)  y = z )
• x y R(x,y)
Example 2
• F = {e,} and P = {}
• e a constant function,  a binary function, 
a binary predicate1
• Model – A set of states,
• A = {binary strings}
• eM = , M concatenation, M prefix
ordering [011 is a prefix of 011001
Example 2
• x ((x  xe)  xe  x))
• y x (y  x)
• x y (y  x)
• x y z ((x  y)  (xz  yz))
• x y ((x  y) (y  x))
Satisfaction
• Given a model M for (F,P) and given an
environment l : var  A the satisfaction
relation M ⊨l 
• P(t1,…,tn)  (a1,…,an) and M ⊨l  iff (a1,…,an)
 RM
• M ⊨l x  iff M ⊨l [x  a] holds for all a  A
• M ⊨l x  iff M ⊨l [x  a] holds for some a
A
Satisfaction
• Given a model M for (F,P) and given an
environment l : var  A the satisfaction
relation M ⊨l 
•
•
•
•
M ⊨l  iff M ⊨l  does not hold
M ⊨l 1  2 iff M ⊨l 1 and M ⊨l 2 holds
M ⊨l 1  2 iff M ⊨l 1 or M ⊨l 2 holds
M ⊨l 1  2 iff M ⊨l 2 holds whenever M
⊨l 1 holds
Semantic Entailment
• For propositional calculus: If for all
valuations (assignments of variables to
truth values) for which all 1,…,n evaluate
to true,  also evaluates to true then the
semantic entailment relation 1,…,n ⊨ 
holds
• Decidable using truth tables
Semantic Entailment
• Let  be a set of formulas (possibly
infinite) and  be a formula from
predicate calculus
•  ⊨  holds iff for all models M and lookup
tables l, whenever M ⊨l  holds for all 
then M ⊨l  holds as well
•  is satisfiable iff there is some model M and
lookup table l such that M ⊨l  holds
•  is valid iff M ⊨l  holds for all models M
and lookup tables l
Soundness and Completeness
• 1,…,n ⊨  holds iff 1,…,n ⊢  is valid
• In particular, ⊨ , a tautology, ⊢  is valid.
I.E.  is a tautology iff  is provable
• Soundness – you can not prove things that are
not true in the truth table sense
• Completeness – you can prove anything that
is true in the truth table sense
Post Correspondence
• Given a finite sequence (s1,t1),…,(sk,tk) of
pairs of binary strings. Is there a sequence
of indices i1,i2,…,in such that si1 sin = ti1
tin
• Example
• s1 = 1, s2 = 10, s3 = 011
• t1 = 101, t2 = 00, t3 = 11
• Solution (1,3,2,3)
• 101110011
• 101110011
Undecidability
• Theorem. The decision problem of validity
for predicate calculus is undecidable: no
program exists which, given any , can
determine in a finite amount of time if ⊨ 
• Proof reduce to Post Correspondence
problem. I.E. show that if the decision
problem is solvable, we could solve the
Post Correspondence problem. This is a
contradiction.
Consequences of Undecidability
• From the soundness and completeness of
predicate logic, which states that ⊨  iff ⊢
, we infer that we can not decide
provability either
• Since  is satisfiable iff  is valid, we
infer that satisfiability for predicate
calculus is also undecidable.
Proof
• Construct a formula  such that ⊨  holds
iff the corresponding Post correspondence
problem has a solution.
•  = 1  2  3
• 1 = i=1..k P(fsi(e),fti(e))
• 2 = vw (P(v,w)  i=1..k P(fsi(v),fti(w)))
• 3 = z P(z,z)
Proof
• Find model which tells us the Post
Correspondence problem has a solution
• eM = empty string
• f0(s) = s0, f1(s) = s1
• PM = {(s,t) | there is a sequence of indices
i1,i2,…,in such that si1 sin = ti1 tin }
• Since ⊨  holds M ⊨  holds
• Both M ⊨ 1 and M ⊨ 2 holds so it
follows that M ⊨ 3 holds. This tells us
there is a solution to the given PC problem
Proof
• Conversely assume that the PCP C has a
solution i1,i2,…,in
• Show that if M is any model having a
constant eM, two unary functions f0M and
f1M, and a binary predicate PM, then the
model has to satisfy 
• Need to show if M ⊨ 1  2 then M ⊨ 3
Proof
•
•
•
•
Encode strings in A
interpret() = eM
interpret(s0) = f0M(interpret(s))
interpret(s1) = f1M(interpret(s))
• Interpret(011) = f1M (f1M (f0M(eM)))
• Since M ⊨ 1, (interpret(si),interpret(ti))  PM
• Since M ⊨ 2, If (s,t)  PM then
(interpret(ssi),interpret(tti))  PM
Proof
• Therefore,
(interpret(si1…sin),interpret(ti1…tin))  PM
• Since i1,i2,…,in is a solution to the PCP
interpret(si1…sin) = interpret(ti1…tin) and z
P(z,z) in M and thus M ⊨ 3
Reachabilty
• When modeling systems via states and
state transitions, we want to show that a
“bad” state can not be reached from a
“good” state.
• Given nodes n and n’ in a directed graph, is
there a finite path of transitions from n to
n’.
s0
s3
A = {s0,s1,s2,s3}
RM = {(s0,s1), (s1,s0), (s1,s1),(s1,s2),
(s2,s0),(s3,s0),(s3,s2)}
s1
s2
Compactness Theorem
• Let  be a set of sentences of predicate
calculus. If all finite subsets of  are
satisfiable, then so is .
• Proof – uses soundness and completeness
and finite length of proofs.
Reachability is Not Expressible
• Can reachability be expressed in predicate
calculus?
• u=v  x (R(u,x)  R(x,v)) 
•
x1x2 (R(u,x1)  R(x1,x2)  R(x2,v))  …
• This is infinite
• The answer is no! Proof follows from
compactness theorem.
Reachability is Not Expressible
• Theorem. There is no predicate-logic
formula  with u and v as its only free
variables and R its only predicate such that
 holds in directed graphs iff there is a
path from u to v.
• Proof. By contradiction. Suppose there is
such a formula. Let n be the formula
expressing that there is a path from c to c’
n = x1 … xn-1 (R(c,x1)  …  R(xn-1,c)).
Reachability is Not Expressible
• Proof. By contradiction. Suppose there is
such a formula . Let n be the formula
expressing that there is a path from c to c’
n = x1 … xn-1 (R(c,x1)  …  R(xn-1,c)).
•  = { i | I  0}  [c/u][c’/v] is
unsatisfiable, but any finite subset is
satisfiable. By compactness this leads to a
contradiction and hence there is no such
.
Reachability via HOL
• Encode Transitive closure
• Pxyz (C1  C2  C3  C4)
•
•
•
•
C1 = P(x,x)
C2 = P(x,y)  P(y,z)  P(x,y)
C3 = P(u,v)  ⊥
C4 = R(x,y)  P(x,y)
• Note quantifier applied to predicate P
(Existential second order logic)
Reachability via HOL
• Obtain formula for the existence of a path
from u to v by negating previous formula
(use DeMorgan’s law)
• Pxyz ( C1   C2   C3   C4)
• If both  and  can range over predicates
then second order logic.