* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PPT
Survey
Document related concepts
Transcript
Complex Structures
Nested Structures
Self referential structures
A structure may have
Data variables
Internal structures/unions
Pointer links
Function pointers
struct course
{
int course_num;
struct student[20];
struct course *next;
int (*average)(int []);
};
Dynamic Structures
Link Lists
A type of data structure that have its elements linked together
Generic on-demand dynamic structure
Easy manipulation, but may not be efficient
Trees
A type of data structures in which elements are connected in a tree form
Complex data structures
More efficient, use only if the number of elements are large
Link Lists
Single Link Lists
head
struct slink {
int data;
struct slink *next;
};
Double Link lists
head
struct dlink {
int data;
struct dlink *next;
struct dlink *prev;
};
Other Link Lists
Hash link lists
bin[size]
Other variants: queues and stacks
Queue: a link list grown at one end, shrink at another, i.e. FIFO
Stack: a LIFO link list
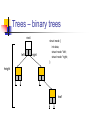
Trees – binary trees
root
left
right
struct node {
int data;
struct node *left;
struct node *right;
};
height
leaf
More Trees
Tertiary Trees
K-ary Trees
Each node has K children
B (Balanced)- Trees
Each node has three children
…
A tree that maintains a balanced height as it grows/shrinks
Sample Usage
Important functions
insert
delete
search
…
Maintain a dynamic structure of sorted numbers using
any of the previous structures
Double link list
void insert (struct dlink *head,
struct dlink *entry)
{
struct dlink * search (struct dlink *head, int val)
{
struct dlink * tmp;
for (tmp = head->next; tmp!= head && tmp->data !=
val; tmp = tmp->next);
return (tmp==head)? NULL : tmp;
struct dlink *tmp;
for (tmp = head->next; tmp!= head && tmp>data < entry->data; tmp = tmp->next);
tmp->prev->next = entry;
entry->prev= tmp->prev;
tmp->prev = entry;
entry->next = tmp;
};
}
int main()
{
struct dlink num[10] = { … };
void delete (struct dlink *entry)
{
struct dlink head={0, NULL, NULL};
for (int i=0; i<10; i++)
insert (&head, &num[i]);
…
return 0;
entry>next->prev = entry->prev;
entry>prev->next = entry->next;
entry->next = entry->prev = NULL;
};
}
Binary Search Tree
void insert (struct node *root,
struct node *entry)
{
/* where to insert is really algorithm dependent.
A generic case only: entry is to replace the left node of
head */
if (head->left) {
entry->left = head->left->left;
entry->right = head->left->right;
}
head->left = entry;
};
void delete (struct node *root, struct node *entry)
{
/* The key is to find a node that has an entry as a child */
};
struct node * search (struct node *root, int val)
{
if (!root)
return NULL;
else if (root->data != val)
tmp = search(root->left, val);
if (!tmp)
tmp = search(root->right, val);
return tmp;
}
int main()
{
struct node num[10] = { … };
struct node root = {0, NULL, NULL};
for (int i=0; i<10; i++) {
insert (&root, &num[i]);
}
…
return 0;