Download Ch 3 Note Sheets L2 S15 Key

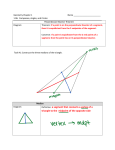
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
3.1 Duplicating Segments and Angles [and Triangles]
These notes replace pages 144 – 146 in the book. You can read these pages for extra clarifications.
Instructions for making geometric figures:
You can sketch a figure without using geometry tools. You need to mark the diagram with equal segments,
equal angles and parallel lines (or parts of lines) or label the measures of the parts to indicate more accurate
measures.
You can draw a figure using measuring tools, such as a protractor and a ruler. Make a drawing when it is
important for lengths and angle measures to be fairly precise. Mark the measures in the diagrams.
You can construct a figure using only a compass and straightedge. When you make a construction, do not
use your measuring tools. You MUST show your “arc marks” to show your work!!
Duplicate will mean to make an exact copy.
Construct a duplicate line segment.
Construct an Equilateral Triangle.
Page 145 Investigation 1: Construct
AB ≅ CD .
Stage 1: Draw a ray longer than AB label endpoint C.
Stage 2: With compass, measure AB and make an arc.
Page 147 #8. Construct equilateral triangle
Stage 3: Put point of compass on point C and make an
arc. Label the intersection D.
sides all equal to AB.
Stage 1: Construct EQ ≅ AB .
Stage 2: With compass equal to AB. Swing an arc with
center E.
Stage 3: With compass equal to AB. Swing an arc with
center Q. Mark the intersection of the two arcs U.
Stage 4: Construct sides EU and QU .
A
B
C
A
D
∆ EQU , with
B
U
Duplicate a triangle. SSS Method.
∆ TRI ≅ ∆ ABC .
Stage 1: Construct TR ≅ AB .
Page 147 #7. Construct
Stage 2: Use compass to measure TI. Swing an arc with
center A.
Stage 3: Use compass to measure RI. Swing an arc with
center B. Mark the intersection of the two arcs C.
Stage 4: Construct sides AC and BC .
I
E
R
T
Q
Can also be used to construct an equiangular
triangle, and to construct a 60° angle.
C
A
S. Stirling
B
Page 1 of 7
Ch 3 Note Sheets S15 KEY
LEVEL 2
3.2 Constructing Perpendicular
Bisectors
Name _________________________
Construct a Perpendicular Bisector
A segment bisector is a line, ray,
or segment that passes through the
midpoint of the segment.
A perpendicular bisector of a
segment is a line (or part of a line)
that passes through the midpoint of
a segment and is perpendicular to
the segment.
A segment has an infinite number of
bisectors, but in a plane it has only
one perpendicular bisector.
Page 150 Investigation 2 Construct
CD , the perpendicular
bisector of AB .
Stage 1: Set compass to a radius longer than 1 AB .
2
Stage 2: With A as center, make an arc above and below AB .
Stage 3: With B as center, make an arc above and below AB .
Label the intersections C and D.
Stage 4: Construct CD . Label intersection M.
A
B
Complete Investigation 1 page 149-150.
Perpendicular Bisector
Conjecture (P 149 Inv 1):
If a point is on the perpendicular
bisector of a segment, then it is
equidistant from the endpoints.
What is point M?
the midpoint
Converse of the Perpendicular Bisector Conjecture:
If a point is equidistant from the endpoints of a segment, then it is on the
perpendicular bisector of the segment.
Given that M is the midpoint of
AB :
E
B
C
Name segment bisectors:
CD , ME , CD , ME , etc…
Name perpendicular bisectors:
M
CD , CD , CM , etc…
A
Since point D is on the perpendicular bisector of
D
AB , AD = DB.
Make a point G that is equidistant from A and B. Where is it?
On the perpendicular bisector.
Is
S. Stirling
AB
a bisector? A perpendicular bisector? Neither
Page 2 of 7
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
3.3 Constructing Perpendiculars to a Line
Read the top of page 154 in the book and the top of page 156 (1st paragraph).
Shortest Distance Conjecture
The shortest distance from a point
to a line is measured along the
perpendicular segment from the
point to the line.
Draw a Perpendicular Line to a line from a point
NOT on the line.
Stage 1: Place your protractor on line j forming a 90º angle and
slide it until the perpendicular ray goes through P.
Stage 2: Draw the perpendicular through P. Label intersection Q.
The distance from a point to a
line is the length of the
perpendicular segment from the
point to the line.
A
R M
Q
j
P
B
S
P
What is the shortest distance
from P to AB ? MP
Is PQ the shortest distance from P to line j?
Yes
Measure the distance from the mall, point M, to each of the major highways that surround the mall.
Use the scale 1 cm = 1 mile. What is the shortest distance from the mall to each route? In other
words, find the distance from point M to each line.
route 2
route 1
M
route 3
S. Stirling
Page 3 of 7
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
Read the rest of page 156 top.
The altitude of a triangle is a
perpendicular segment from a vertex of a
triangle to the line containing the
opposite side.
Draw all Altitudes [in an acute triangle].
The length of this segment is the height
of the triangle.
A triangle has three sides, so it has three
different altitudes and it has three different
heights! In the figures, use a colored pencil to
indicate the heights, draw the altitudes, from
each side of the triangle. Use a note card or
protractor to help you! You may also want to
turn the triangle around so that the segment you
are drawing the altitude to is parallel to you.
Draw all Altitudes [in a right triangle].
Where are all of the altitudes located?
All inside the triangle.
Draw all Altitudes [in an obtuse triangle].
You will need to extend the sides BO
and TO in order to draw the altitudes!!
Where are all of the altitudes located?
Where are all of the altitudes located?
One inside and 2 on the sides of the
triangle (the legs).
One inside and 2 outside the triangle.
As you can see, an altitude can be inside or outside the triangle, or it can be one of the triangle’s
sides. It all depends on the shape of the triangle.
T
T
A
L
A
R
A
L
R
Acute ∆ TRA with altitude AL .
AL is the height from base RT .
S. Stirling
Right ∆ TRA with altitude
AT .
AT is the height from base RT .
R
Obtuse ∆ TRA with altitude
AL
is the height from base
Page 4 of 7
T
AL
RT
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
3.4 Constructing Angle Bisectors
Read the top of page 159 in the book. Complete
Investigation 1 page 159, need tracing paper.
P
Angle Bisector Conjecture If a point
is on the bisector of an angle, then it
is equidistant from the sides of the
angle.
If A is on angle bisector QA ,
then XA = AY.
X
A
Q
or A is equidistant from QP and QR .
Y
R
Does every angle have a bisector? Yes
Is it possible for an angle to have more than one bisector? No, only one.
Is the converse true?
Converse of Angle Bisector Conjecture
If a point is equidistant from the sides of the angle, then it is on the
bisector of an angle.
To show that the converse works, find a point equidistant from the sides of angle
BC and a point F on BA that
is the same distance from B. So BE = BF .
∠ ABC :
1. Place a point E on
A
2. Draw perpendiculars through points E and F.
Label the intersection X.
Is X equidistant from the sides of the angle? How do
you know?
Yes. The distance from a point to a line is
measured along the perpendicular from the
point to the line.
Is
XE = XF
B
C
? YES
BX . Is it the bisector of ∠ ABC ? YES
Measure ∠ CBX and ∠ XBA to confirm. 21º
Draw
S. Stirling
Page 5 of 7
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
3.5 Drawing Parallel Lines
What properties do you have that can guarantee you parallel lines?
If the alternate interior angles are equal, or the corresponding angles are equal, or the same-side
interior angles are supplementary, then the lines are parallel.
1. Draw a line parallel to n through P using
alternate interior angles. Label what you
measured and state the property you used.
2. Draw a line parallel to n through P using
corresponding angles. Label what you
measured and state the property you used.
n
n
P
P
3. Draw a line parallel to n through P using
same-side interior angles. Label what you
measured and state the property you used.
n
107
P
73
S. Stirling
Page 6 of 7
Ch 3 Note Sheets S15 KEY
LEVEL 2
Name _________________________
Misc. EXERCISES
Problem Solving:
A. Three towns’ fire stations are shown on the map below. They are planning to join each with
straight access roads and then need to locate a central communication tower that is equidistant
from the three roads. Find the location of the communication tower and explain to the planners
why you know that it is the correct location.
The three roads form a
triangle.
Create the angle bisectors
to find a point equidistant
from the sides of the
triangle, so the tower will
be equidistant from the 3
roads.
A point on the bisector of
an angle is equidistant
from the sides of the angle.
B. Three towns’ fire stations are shown on the map below. They are planning to consolidate their
resources and need to locate a central communication center that is equidistant from the three fire
stations. Find the location of the communication center and explain to the planners why you
know that it is the correct location.
The three roads form a
triangle.
Create the perpendicular
bisectors of the sides to find
points equidistant from the
endpoints. The point is
equidistant from the
vertices of the triangle, so
the tower will be equidistant
from the 3 fire stations.
A point on the bisector of a
segment is equidistant from
the endpoints of the
segment.
S. Stirling
Page 7 of 7