Download Discrete Random Variables

Statistics 215 Lab Materials
Discrete Random Variables
In this chapter, we introduce a new concept that of a random variable or RV. A random variable is a model
to help us describe the state of the world around us. Roughly, a RV can be thought of as the value that is
assigned to the outcome of an experiment. There are different RVs depending upon the type of quantity
that we are trying to model. In this chapter we will introduce some random variables for experiments
whose outcome is a whole number. In the next chapter we will discuss random variables whose values are
any number within an interval. Both of these chapters focus on numeric random variables. That is, the
outcomes that the experiment in question produces are numbers.
Sample and Population notation
Before we begin with random variables, it is important that we specify some new notation that
differentiates the data analysis that we were doing in Chapters 1 through 3 and what we will do throughout
the rest of the course. We are going to differentiate between the population mean and the sample mean.
The population mean is the mean or average of all the elements of the population. The sample mean is the
average for a subset of that population. Thus we need notation to demarcate between these two ideas. For a
variable X, the population mean we will use the Greek symbol mu with a subscript of x, µx. For the sample
mean, we have already seen that we will use the symbol x with a bar over it or x . We will do the same for
the standard deviation. For a variable X, the population standard deviation will be the Greek letter sigma
with a subscript of x, σx. The sample standard deviation will be denoted by the letter s with a subscript of
x, sx.
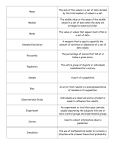
Quantity
Mean
Standard Deviation
Population Parameter
µx
σx
Sample Statistic
x
sx
Example
Suppose that the population is made up of 25 students in a Stat 101 lab and the variable that we are
interested in is the number of siblings for each student, call it Y.
y:4,3,1,1,5,2,2,4,0,2,1,2,3,0,2,4,4,6,0,0,1,3,3,1,3
The population mean µy is 2.28 and the population standard deviation is σy = 1.646.
If we take a sample from this population of 5 individuals, we might get 1,2,2,3,0.
The mean of this sample is y =1.6 and the standard deviation is sy=1.14.
If another samples is drawn then we might get 4, 1, 0, 2, 4.
The mean of this sample is y =2.1 and the standard deviation is sy = 1.79
Random Variables
Definition: A random variable or RV is a variable whose value is determined by the outcome of an
experiment.
Examples:
W = the number of tomatoes that a plant will produce
I = the inflation rate for the U.S. in the fourth quarter of this year
Page 1 of 5
Statistics 215 Lab Materials
Z = the number of people who vote in the next presidential election
T = number of tablets in a bottle of aspirin
K = number of potatoes in a 5 pound bag of potatoes
B = time between phone calls for a computer helpline
There are two types of random variables discrete and continuous.
Definition: A random variable is called discrete if it can only take a countable number of values.
Example:
In the list of RVs above, W, Z, T, and K are all discrete random variables.
Definition: A random variable is called continuous if it can take values inside an interval.
Example:
In the list of RVs above, I and B are continuous random variables.
Definition: A probability distribution (sometimes simply called a distribution) is the mechanism that
assigns probabilities to each value that the random variable can assume.
Discrete Random Variables
In this chapter we will focus on discrete random variables.
Notation: For a discrete RV X, we will use as shorthand P(X=x) to represent the probability that the
variable X takes the value x. Often we will make this even shorter and simply write p(x).
Example:
For a six-sided die with the values {1, 2, 3, 4, 5, 6} on it’s faces, let X be the value that appears on the face
when the die is rolled. Then p(2) or P(X=2) represents the probability that X will be 2.
Rules
There are two rules for all discrete probability distributions:
1. 0 ≤ P(X=x) ≤ 1 for each value of x.
2. Σ P(X=x) = 1
These rules imply that each event has a probability between 0 and 1 and that if we add up all the possible
events their sum must be 1.
We can use several methods for describing the distribution of a random variable X
1. Table
For the table each possible value that the RV may take is listed and below it is listed the probability
associated with that value.
Page 2 of 5
Statistics 215 Lab Materials
Example:
y
P(Y=y)
2
0.3
3
0.2
4
0.5
From this table we can see that the probability that the RV Y takes the value 3 is 0.2 or P(Y=3) =0.2.
We can also note that P(Y=2) = 0.3.
2. Line graph
The second possible way to represent a distribution is through a line graph.
For a line graph each possible value that the RV can take is listed on the x-axis. Vertical lines are drawn up
from each possible value so that the height of those lines corresponds to the probability of that value.
Example:
For the RV X
x
P(X=x)
2
0.4
3
0.1
4
0.2
5
0.3
The line graph for this distribution of X looks like the following:
P(X=x)
0.30
0.10
1
2
3
w
4
5
3. Formula
Lastly we can use a formula to describe the distribution of a random variable. Under this method, if we
know certain quantities, usually called parameters, then we can calculate the probability of a particular
value for the RV.
Example:
P(X=x) = v(1-v)x-1 for x = 1, 2, 3, . . .
If we know what v is we can then calculate the probabilities for each value of x. In this example the
parameter we would need to know would be v.
Theoretical Mean (Expected Value) of a Discrete Probability Distribution
If we know the probability distribution of a discrete random variable, we can compute its theoretical mean
(also called the population mean) directly. There is no need to obtain a random sample, calculate the
sample mean, and then use the sample mean to estimate the theoretical (or population) mean.
E(X) = µ = Σ(x * p(x))
€
Page 3 of 5
Statistics 215 Lab Materials
For the RV X with probability distribution:
x
P(X=x)
2
0.4
3
0.1
4
0.2
5
0.3
E(X) = µ = Σ(x * p(x))
= 2 * 0.4 + 3* 0.1+ 4 * 0.2 + 5 * 0.3
= 3.4
€
Theoretical Standard Deviation of a Discrete Probability Distribution
€
If we know the probability distribution of a discrete random variable, we can compute its theoretical
variance and theoretical standard deviation directly.
VAR(X) = σ 2 = Σ(x − µ) 2 * p(x)
An alternate formula for computing the theoretical variance is
€
VAR(X) = σ 2 = [Σx 2 * p(x)] − µ 2
The theoretical standard deviation is the square root of the theoretical variance.
€
S.D(X) = σ = Σ(x − µ) 2 * p(x)
or
€
S.D.(X) = σ =
€
[Σx
2
* p(x)] − µ 2
For the RV X with probability distribution:
x
P(X=x)
2
0.4
3
0.1
4
0.2
5
0.3
VAR(X) = σ 2 = Σ(x − µ) 2 * p(x)
= (2 − 3.4) 2 * 0.4 + (3 − 3.4) 2 * 0.1+ (4 − 3.4) 2 * 0.2 + (5 − 3.4) 2 * 0.3
= 0.784 + 0.016 + 0.072 + 0.768
= 1.64
€
Page 4 of 5
Statistics 215 Lab Materials
So the theoretical standard deviation is
S.D.(X) = σ = Σ(x − µ) 2 * p(x)
= 1.64
= 1.2806
€
Using the alternate formulas for theoretical variance and theoretical standard deviation, we will obtain the
same answers as above.
VAR(X) = σ 2 = [Σx 2 * p(x)] − µ 2
= 2 2 * 0.4 + 32 * 0.1+ 4 2 * 0.2 + 5 2 * 0.3 − 3.4 2
= 1.6 + 0.9 + 3.2 + 7.5 −11.56
= 1.64
and
€
[Σx
S.D.(X) = σ =
2
* p(x)] − µ 2
= 1.64
= 1.2806
The Cumulative Distribution Function of a Discrete Random Variable
€
The Cumulative Distribution Function (CDF) of a Discrete Random Variable specifies the probability that
a random variable X is less than or equal to some specified value x. The CDF is usually indicated by F(x)
and is defined as
F(x) = P(X ≤ x)
and is computed as
€
F(x) = Σ P(X = t)
t ≤x
For the RV X with probability distribution:
€
x
P(X=x)
2
0.4
3
0.1
4
0.2
5
0.3
we could add another row to this table for the CDF of W
x
P(X=x)
F(x)
2
0.4
0.4
3
0.1
0.5
4
0.2
0.7
Page 5 of 5
5
0.3
1.0