Download Descriptive Statistics

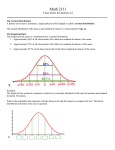
Descriptive Statistics
Part 4 – Measures of Dispersion
A measure of location, such as the mean or the median, only describes the centre of the data.
It is valuable from that standpoint, but it does not tell us anything about the spread of the
data.
For example, if someone told you that a river averaged 3 feet in depth, would you want to
wade across on foot without additional information? Probably not, you would want to know
something about the variation in the depth. Is the maximum depth of the river 3.25 feet and
the minimum 2.75 feet? If that is the case, you would probably agree to cross. What if you
learned that the river depth ranged from 0.50 feet to 5.5 feet? Your decision would probably
be not to cross. Before making a decision about crossing the river, you want information on
both the typical depth and the dispersion in the depth of the river.
A small value for a measure of dispersion indicates that the data are clustered closely, say,
around the arithmetic mean. The mean is therefore considered representative of the data.
Conversely, a large measure of dispersion indicates that the mean is not reliable. Look at
Figure 1 below.
The 100 employees of this company are organized into a histogram based on the number of
years of employment with the company. The mean is 4.9 years, but the spread of the data is
from 6 months to 16.8 years. The mean of 4.9 years is not very representative of all the
employees.
A second reason for studying the dispersion in a set of data is to compare the spread in two or
more distributions. Suppose, for example, that Sony assembles TVs in Japan and US. The
arithmetic mean hourly output in both the Japanese plant and the US plant is 50.
Based on the two means, you might conclude that the distributions of the hourly outputs are
identical. Production records for 9 hours at the two plants, however, reveal that this
conclusion is not correct (see Figure 2).
Japanese production varies from 48 to 52 assemblies per hour. Production at the US plant is
more erratic, ranging from 40 to 60 per hour. Therefore, the hourly output for Japan is
clustered near the mean of 50; the hourly output for the US is more dispersed.
Example:
The table below presents the payoff matrix of an investment A and an investment B and
shows how the expected value or mean of each investment is determined.
Investment
A
(1)
(2)
(3)
(4)
State of Economy
Probability of Occurrence
Outcome of Investment
Expected Value (2) x (3)
Boom
0.25
€600
€150
Normal
0.50
€500
€250
Recession
0.25
€400
€100
Expected Earnings from Investment A
B
€500
Boom
0.25
€800
€200
Normal
0.50
€500
€250
Recession
0.25
€200
€50
Expected Earnings from Investment B
€500
In this case the expected value of each of the two investments is €500, but the range of
outcomes or payoffs for investment A (from €400 in recession to €600 in boom) is much
smaller than for investment B (from €200 in recession to €800 in boom)
The expected profit and the variability in the outcomes of investment A and investment B are
shown in the chart below, where the height of each bar measures the probability that a
particular outcome (measured along the horizontal axis) will occur.
Note that the relationship between the state of the economy and profits is much tighter (i.e.
less dispersed) for investment A than for investment B. Therefore, investment A is less risky
than investment B. Since both investments have the same expected profit, investment A is
preferable to investment B.
We will consider several measures of dispersion. The range is based on the largest and the
smallest values in the data set, that is, only two values are considered. The mean deviation,
the variance, and the standard deviation use all the values in a data set and are all based on
deviations from the arithmetic mean.
Range
The simplest measure of dispersion is the range. It is the difference between the largest and
the smallest values in a data set. In the form of an equation:
ange
argest alue
mallest alue
Example:
Using Figure 2, find the range in the number of TVs produced per hour for the Japan and the
USA plants. Interpret the two ranges.
The range of the hourly production of TVs at the Japanese plant is 4, found by the difference
between the largest hourly production of 52 and the smallest of 48. The range in the hourly
production for the US plant is 20 TVs, found by 60 - 40.
We therefore conclude that (1) there is less dispersion (spread) in the hourly production in the
Japanese plant than in the US plant because the range of 4 TVs is less than a range of 20 TVs,
and (2) the production is clustered more closely around the mean of 50 at the Japanese plant
than at the US plant (because a range of 4 is less than a range of 20).
Therefore, the mean production in the Japanese plant (50 TVs) is a more representative
measure of location than the mean of 50 TVs for the US plant.
Mean Deviation
A defect of the range is that it is based on only two values, the highest and the lowest; it does
not take into consideration all of the values. The mean deviation does. It measures the mean
amount by which the values in a population, or sample, vary from their mean. In terms of a
definition:
Mean Deviation: The arithmetic mean of the absolute values of the deviations from the
arithmetic mean.
In terms of a formula, the mean deviation is computed for a sample by:
where:
X
n
| |
=
=
=
=
the value of each observation
the arithmetic mean of the values
the number of observations in the sample
indicates the absolute value i.e. we ignore the signs of the deviations
from the mean so it will always be positive
Why do we ignore the signs of the deviations from the mean? If we didn’t, the positive and
negative deviations from the mean would exactly offset each other, and the mean deviation
would always be zero. Such a measure (zero) would be a useless statistic.
Example:
The number of cappuccinos sold at the Starbucks on the Grafton Street between 4 and 7 p.m.
for a sample of 5 days last year were 20, 40, 50, 60, and 80.
On Dawson Street, the number of cappuccinos sold at Starbucks between 4 and 7 p.m. for a
sample of 5 days last year were 20, 49, 50, 51, and 80.
Determine the mean, median, range, and mean deviation for each location. Compare the
differences.
For the Grafton Street location the mean, median, and range are:
Mean
Median
Range
Cappuccinos Per Day
50
50
60
The mean deviation is the mean of the absolute differences between individual observations
and the arithmetic mean. For Grafton Street, the mean number of cappuccinos sold is
50, found by (20 + 40 + 50 + 60 + 80)/5. Next we find the differences between each
observation and the mean. Then we sum these differences, ignoring the signs, and divide the
sum by the number of observations. The result is the mean difference between the
observations and the mean.
The mean deviation is 16 cappuccinos per day and shows that the number of cappuccinos
sold deviates, on average, by 16 from the mean of 50 cappuccinos per day.
You can do the same for the Dawson Street shop and come up with:
Mean
Median
Range
Mean Deviation
Cappuccinos Per Day
50
50
60
12.4
Recall previously that we described data using graphical methods. Here we are describing
data using numerical measures. When we use numerical measures, it is very important to
always report measures of location and dispersion.
Let us interpret and compare the results of our measures for the Starbucks locations. The
mean and median of the two locations are exactly the same, 50 cappuccinos per day.
Therefore, the location of both distributions is the same. The range for both locations is also
the same, 60. However, recall that the range provides limited information about the
dispersion of the distribution.
Notice that the mean deviations are not the same because they are based on the differences
between all observations and the arithmetic mean, which show the relative closeness or
clustering of the data relative to the mean or centre of the distribution. Compare the mean
deviation for Grafton Street shop of 16 to the mean deviation for Dawson Street of 12.4.
Based on the mean deviation, we can say that the dispersion for the sales distribution of the
Dawson Street Starbucks is more concentrated near the mean of 50 than the Grafton Street
shop.
The mean deviation has two advantages. First, it uses all the values in the computation
whereas the range uses only the highest and the lowest values. Second, it is easy to
understand - it is the average amount by which values deviate from the mean. However, its
drawback is the use of absolute values. Generally, absolute values are difficult to work with
and to explain, so the mean deviation is not used as frequently as other measures of
dispersion, such as the standard deviation.
Variance and Standard Deviation
The variance and standard deviation are also based on the deviations from the mean.
However, instead of using the absolute value of the deviations, the variance and the standard
deviation square the deviations.
Variance: The arithmetic mean of the squared deviations from the mean.
Standard Deviation: The square root of the variance.
Population Variance
The formulas for the population variance and the sample variance are slightly different. The
population variance is considered first. (Recall that a population is the totality of all
observations being studied.) The population variance is found by:
where:
=
X
N
=
=
=
the population variance (is the lowercase Greek letter sigma). It is read
as “sigma squared.”
the value of an observation in the population.
the arithmetic mean of the population.
the number of observations in the population.
Note the process of computing the variance.




We begin by finding the mean.
Next we find the difference between each observation and the mean, and square that
difference.
Then we sum all the squared differences.
And finally we divide the sum of the squared differences by the number of items in
the population.
So you might think of the population variance as the mean of the squared difference between
each value and the mean. For populations whose values are near the mean, the variance will
be small. For populations whose values are dispersed from the mean, the population variance
will be large.
The variance overcomes the weakness of the range by using all the values in the population,
whereas the range uses only the largest and the smallest. We overcome the issue where
by squaring the differences, instead of using the absolute values. Squaring the
differences will always result in non-negative values.
Example:
The number of parking tickets issued last year by month in Cork City is reported below.
Month
Tickets
January
19
February
17
March
22
April
18
May
28
June
34
July
45
August
39
September
38
October
44
November
34
December
10
Determine the population variance.
Because we are studying all the tickets for a year, the data is a population. To determine the
population variance, we use the formula. The table below details the calculations.
Month
Tickets
X-µ
(X - µ)2
-10
-12
100
144
January
February
X
19
17
March
22
-7
49
April
18
-11
121
May
28
-1
1
June
34
5
25
July
August
45
39
16
10
256
100
September
38
9
81
October
44
15
225
November
34
5
25
December
10
-19
361
Total
348
0
1,488
X - µ)2
1. We begin by determining the arithmetic mean of the population. The total number of
tickets issued for the year is 348, so the mean number issued per month is 29.
2. Next we find the difference between each observation and the mean. This is shown in
the third column of the table. Recall that earlier we said that the sum of the
differences between each value and the mean is 0. From the spreadsheet, the sum of
the differences between the mean and the number of tickets each month is 0.
3. The next step is to square the difference between each monthly value. That is shown
in the fourth column of the table. By squaring the differences, we convert both the
positive and the negative values to a plus sign. Hence, each difference will be
positive.
4. The squared differences are totalled. The total of the fourth column is 1,488. That is
the term (X - µ)2
5. Finally, we divide the squared differences by N, the number of observations in the
population.
So, the population variation for the number of tickets is 124.
Like the range and the mean deviation, the variance can be used to compare dispersion in two
or more sets of observations.
For example, the variance for the number of tickets issued in Cork City above was just
computed to be 124. If the variance in the number of tickets issued in Dublin City is 342.9,
we conclude that (1) there is less dispersion in the distribution of the number of tickets issued
in Cork City than in Dublin City (because 124 is less than 342.9); and (2) the number of
tickets in Cork City is more closely clustered around the mean of 29 than for the number of
tickets issued in Dublin City. Therefore, the mean number of tickets issued in Cork City is a
more representative measure of location than the mean number of tickets in Dublin City.
Population Standard Deviation
Both the range and the mean deviation are easy to interpret. The range is the difference
between the high and low values of a set of data, and the mean deviation is the mean of the
deviations from the mean. However, the variance is difficult to interpret for a single set of
observations. The variance of 124 for the number of tickets issued is not in terms of tickets,
but tickets squared.
There is a way out of this difficulty. By taking the square root of the population variance, we
can transform it to the same unit of measurement used for the original data. The square root
of 124 tickets-squared is 11.14 tickets. The units are now simply tickets. The square root of
the population variance is the population standard deviation:
Sample Variance
The formula for the population mean is
. We just changed the symbols for the sample
mean; that is,
. Unfortunately, the conversion from the population variance to the
sample variance is not as direct. It requires a change in the denominator. Instead of
substituting n (number in the sample) for N (number in the population), the denominator is n
- 1. Thus the formula for the sample variance is:
where:
s2
X
n
=
=
=
=
the sample variance
the value of each observation in the sample
the mean of the sample
the number of observations in the sample
Why is this change made in the denominator? Although the use of n is logical since is used
to estimate , it tends to underestimate the population variance, . The use of (n - 1) in the
denominator provides the appropriate correction for this tendency. Because the primary use
of sample statistics like s2 is to estimate population parameters like , (n - 1) is preferred to
n in defining the sample variance. We will also use this convention when computing the
sample standard deviation.
Example:
The hourly wages for a sample of part-time employees at Home Depot are: €12, €20, €16,
€18, and €19. What is the sample variance?
Sample Standard Deviation
The sample standard deviation is used as an estimator of the population standard deviation.
As noted previously, the population standard deviation is the square root of the population
variance. Likewise, the sample standard deviation is the square root of the sample variance.
The sample standard deviation is most easily determined by:
The Standard Deviation of Grouped Data
In most instances measures of location, such as the mean, and measures of dispersion, such as
the standard deviation, are determined by using the individual values. Statistical software
packages make it easy to calculate these values, even for large data sets. However, sometimes
we are given only the frequency distribution and wish to estimate the mean or standard
deviation.
It must be stressed that a mean or a standard deviation from grouped data is an estimate of the
corresponding actual values.
To calculate the standard deviation of data grouped into a frequency distribution, we need to
adjust the formula slightly. We weight each of the squared differences by the number of
frequencies in each class. The formula is:
where:
s
M
f
n
=
=
=
=
=
the sample standard deviation
the class midpoint
class frequency
the mean of the sample
the number of observations in the sample
Example:
Given the frequency distribution for car prices below, compute the standard deviation of car
selling prices.
Frequency Distribution of Selling Prices
Class
€15,000 up to €17,999
€18,000 up to €20,999
€21,000 up to €23,999
€24,000 up to €26,999
€27,000 up to €29,999
€30,000 up to €32,999
€33,000 up to €35,999
Total
Frequency
8
23
17
18
8
4
2
80
Step 1: Find the midpoint of each class. Recall that the midpoint of a class is halfway between
the lower limits of two consecutive classes. It is computed by adding the lower limits
of consecutive classes and dividing the result by 2. Referring to the table above, for
the first class the lower class limit is €15,000 and the next limit is €18,000. The class
midpoint is €16,500, found by (€15,000 - €18,000)/2.
Step 2: Compute the arithmetic mean for the distribution.
Frequency
(f)
8
23
17
18
8
4
2
80
Selling Price Class
€15,000 up to €17,999
€18,000 up to €20,999
€21,000 up to €23,999
€24,000 up to €26,999
€27,000 up to €29,999
€30,000 up to €32,999
€33,000 up to €35,999
Total
Midpoint
(X)
€16,500
€19,500
€22,500
€25,500
€28,500
€31,500
€34,500
fX
€132,000
€448,500
€382,500
€459,000
€228,000
€126,000
€69,000
€1,845,000
ΣfX
Solving for the arithmetic mean we get:
Σ
Step 3: Subtract the mean from the class midpoint. That is, find
(16,500 23,062.50 = -6,562.50)
For the first class
Selling Price Class
€15,000 up to €17,999
€18,000 up to €20,999
€21,000 up to €23,999
€24,000 up to €26,999
€27,000 up to €29,999
€30,000 up to €32,999
€33,000 up to €35,999
Total
Frequency Midpoint
Mean
(f)
(M)
8
€16,500 €23,062.50 -€6,562.50
23
€19,500 €23,062.50 -€3,562.50
17
€22,500 €23,062.50 -€562.50
18
€25,500 €23,062.50 €2,437.50
8
€28,500 €23,062.50 €5,437.50
4
€31,500 €23,062.50 €8,437.50
2
€34,500 €23,062.50 €11,437.50
80
Step 4: Square the difference between the class midpoint and the mean.
Selling Price Class
€15,000 up to €17,999
€18,000 up to €20,999
€21,000 up to €23,999
€24,000 up to €26,999
€27,000 up to €29,999
€30,000 up to €32,999
€33,000 up to €35,999
Total
Frequency Midpoint
Mean
(f)
(M)
8
€16,500 €23,062.50 -€6,562.50 €43,066,406.25
23
€19,500 €23,062.50 -€3,562.50 €12,691,406.25
€316,406.25
17
€22,500 €23,062.50 -€562.50
€5,941,406.25
18
€25,500 €23,062.50 €2,437.50
8
€28,500 €23,062.50 €5,437.50 €29,566,406.25
4
€31,500 €23,062.50 €8,437.50 €71,191,406.25
2
€34,500 €23,062.50 €11,437.50 €130,816,406.25
80
Step 5: Multiply the squared difference between the class midpoint and the mean by the class
frequency and sum.
Selling Price Class
€15,000 up to
€17,999
€18,000 up to
€20,999
€21,000 up to
€23,999
€24,000 up to
€26,999
€27,000 up to
€29,999
€30,000 up to
€32,999
€33,000 up to
€35,999
Frequency
Midpoint
Mean
(f)
(M)
8
€16,500
€23,062.50
-€6,562.50
€43,066,406.25
€344,531,250.0
23
€19,500
€23,062.50
-€3,562.50
€12,691,406.25
€291,902,343.7
17
€22,500
€23,062.50
-€562.50
€316,406.25
€5,378,906.25
18
€25,500
€23,062.50
€2,437.50
€5,941,406.25
€106,945,312.5
8
€28,500
€23,062.50
€5,437.50
€29,566,406.25
€236,531,250.0
4
€31,500
€23,062.50
€8,437.50
€71,191,406.25
€284,765,625.0
2
€34,500
€23,062.50 €11,437.50 €130,816,406.25
€261,632,812.5
Total
€1,531,687,500.
80
To find the standard deviation we insert these values into the formula
€
€
The standard deviation calculated from the data grouped into a frequency distribution will
usually be close to the value calculated from raw data. The grouped data result in some loss
of information. For the raw car price data the standard deviation is €4,354.44. The standard
deviations differ by about €49 or 1.1 percent. Based on the percentage difference, the
estimate is very close to the actual value.
Interpretation and Uses of the Standard Deviation
Chebyshev’s Theorem
We have stressed that a small standard deviation for a set of values indicates that these values
are located close to the mean. Conversely, a large standard deviation reveals that the
observations are widely scattered about the mean. The Russian mathematician P. L.
Chebyshev (1821 1894) developed a theorem that allows us to determine the minimum
proportion of the values that lie within a specified number of standard deviations of the mean.
For example, according to Chebyshev’s Theorem, at least three of four values, or 75 percent,
must lie between the mean plus two standard deviations and the mean minus two standard
deviations.
This relationship applies regardless of the shape of the distribution. Further, at least eight of
nine values, or 88.9 percent, will lie between plus three standard deviations and minus three
standard deviations of the mean.
At least 24 of 25 values, or 96 percent, will lie between plus and minus five standard
deviations of the mean.
Chebyshev’s theorem states: For any set of observations (sample or population), the
proportion of the values that lie within k standard deviations of the mean is at least 1 - 1/k2,
where k is any constant greater than 1.
Example:
The arithmetic mean monthly price of cars sold by a dealership €23,218, and the standard
deviation is €4.354.44.
At least what percent of the contributions lie within plus 3.5 standard deviations and minus
3.5 standard deviations of the mean?
Therefore, at least 92% of the prices lie within plus 3.5 standard deviations and minus 3.5
standard deviations of the mean.
The Empirical Rule
Chebyshev’s theorem is concerned with any set of values; that is, the distribution of values
can have any shape. However, for a symmetrical, bell-shaped distribution such as the one in
the figure below, we can be more precise in explaining the dispersion about the mean. These
relationships involving the standard deviation and the mean are described by the Empirical
Rule, also called the Normal Rule.
Empirical(Normal) Rule: For a symmetrical, bell-shaped frequency distribution,
approximately 68 percent of the observations will lie within plus and minus one standard
deviation of the mean; about 95 percent of the observations will lie within plus and minus
two standard deviations of the mean; and practically all (99.7 percent) will lie within plus and
minus three standard deviations of the mean.
These relationships are portrayed graphically below for a bell-shaped distribution with a
mean of 100 and a standard deviation of 10.
It has been noted that if a distribution is symmetrical and bell-shaped, practically all of the
observations lie between the mean plus and minus three standard deviations. Thus, if = 100
and s = 10, practically all the observations lie between 100 + 3(10) and 100 - 3(10), or 70 and
130.
Example:
A sample of the rental rates in an apartment complex approximates a symmetrical, bellshaped distribution. The sample mean is €500; the standard deviation is €20. Using the
Empirical Rule, answer these questions:
1. About 68 percent of the monthly food expenditures are between what two amounts?
2. About 95 percent of the monthly food expenditures are between what two amounts?
3. Almost all of the monthly expenditures are between what two amounts?
1. About 68 percent are between $480 and $520, found by:
1 tandard Deviation €500
€
2. About 95 percent are between $460 and $540, found by:
2 tandard Deviations €500
€
3. Almost all (99.7 percent) are between $440 and $560, found by;
3 tandard Deviations €500
€