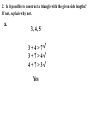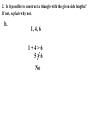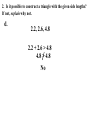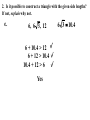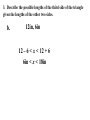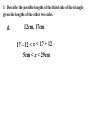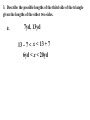* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Slide 1 - msmatthewsschs
Penrose tiling wikipedia , lookup
Golden ratio wikipedia , lookup
Multilateration wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
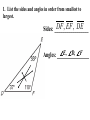
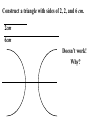
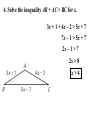
5.5 – Use Inequalities in a Triangle P 95º 5cm 2.2cm 55º M 30º 5.9cm N Measure each side of the triangle in centimeters and each angle in degrees. Write these measurements on your triangle. Theorem: If one ______ side of the triangle is longer than the other side, then the angle opposite larger ____________ the __________ longer side is _________ opposite shorter than the angle ____________ the ____________ side angle Theorem: If one _________ of a triangle is larger __________ than another angle, then the side larger opposite the _____________ angle is longer ___________ than the side opposite the smaller angle. 1. List the sides and angles in order from smallest to largest. AB, BC , AC Sides: _________________ C, A, B Angles: ________________ 1. List the sides and angles in order from smallest to largest. ST , RT , SR Sides: _________________ R, S, T Angles: ________________ 1. List the sides and angles in order from smallest to largest. KJ , KH , JH Sides: _________________ H, J, K Angles: ________________ 55° 1. List the sides and angles in order from smallest to largest. DF , EF , DE Sides: _________________ 33° E, D, F Angles: ________________ Construct a triangle with sides of 2, 2, and 6 cm. 2cm 6cm Doesn’t work! Why? 2cm 2cm 6cm Too short! What if I tried 3, 3, and 6cm? 3cm 3cm 6cm Still doesn’t work! Triangle Inequality Theorem: The sum of the lengths of any two sides of a triangle is greater than the length of the third side. a+b>c a+c>b b+c>a c a b 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. a. 3, 4, 5 3+4>7 3+7>4 4+7>3 Yes 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. b. 1, 4, 6 1+4>6 5>6 No 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. c. 17, 17, 33 17 + 17 > 33 17 + 33 > 17 17 + 33 > 17 Yes 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. d. 2.2, 2.6, 4.8 2.2 + 2.6 > 4.8 4.8 > 4.8 No 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. e. 6, 6 3, 12 6 + 10.4 > 12 6 + 12 > 10.4 10.4 + 12 > 6 Yes 6 3 10.4 2. Is it possible to construct a triangle with the given side lengths? If not, explain why not. f. 7, 52, 45 7 + 52 > 45 7 + 45 > 52 52 > 52 No 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. a. x + 9 > 21 x > 12 21 + 9 > x 30 > x or x < 30 12 < x < 30 x + 21 > 9 x > -12 Trick! Subtract the two sides to find the lowest and add to find the highest. 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. b. 12in, 6in 12 – 6 < x < 12 + 6 6in < x < 18in 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. c. 3ft, 8ft 8–3< x< 8+3 5ft < x < 11ft 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. d. 12cm, 17cm 17 – 12 < x < 17 + 12 5cm < x < 29cm 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. e. 7yd, 13yd 13 – 7 < x < 13 + 7 6yd < x < 20yd 3. Describe the possible lengths of the third side of the triangle given the lengths of the other two sides. f. 9m, 9m 9–9< x< 9+9 0m < x < 18m 4. Solve the inequality AB + AC > BC for x. 5 + 7 > 2x – 2 12 > 2x – 2 14 > 2x 7>x x<7 4. Solve the inequality AB + AC > BC for x. 3x + 1 + 4x – 2 > 5x + 7 7x – 1 > 5x + 7 2x – 1 > 7 2x > 8 x>4