Download Triangle inequalities Objective: To use inequalities

PROGRESS REPORTS TERM 2 – DEC 12TH
1.
2.
3.
4.
TRIANGLE INEQUALITIES
OBJECTIVE:
TO USE INEQUALITIES INVOLVING THE
SIDES AND ANGLES OF TRIANGLES
5.
AGENDA
Warm Up
Quiz Return
Notes
Whiteboard
Practice
Exit Ticket
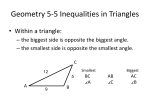
THEOREM
In a triangle, the longest side is across
from the largest angle.
In a triangle, the shortest side is across
from the smallest angle.
PRACTICE
 Example #1: Order the angles from smallest to largest.
 Example #2 Order the angles from smallest to largest
THEOREM
The sum of the lengths of any two sides of
a triangle must be greater than the third
side.
b
a
c
a+b> c
b+c > a
a+c > b
If these inequalities are NOT true, you do
not have a triangle!
FINDING “POSSIBLE” LENGTHS
 Suppose we know the lengths of two sides of a
triangle, and we want to find the “possible” lengths
of the third side.
IS IT A TRIANGLE?
*REMEMBER*: THE SUM OF ANY 2 SIDES OF A TRIANGLE IS GREATER THAN THE THIRD SIDE.
Decide whether each set of numbers is a triangle.
3. {3,4,5}
4. {3,5,10}
5. {5,5,10}
EXAMPLE #6
The measures of two sides are given.
Between what two numbers must the third
side fall? Write an inequality to represent
your answer.
9 and 15