* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download WHAT IS AN ALGORITHM?
Abstraction (computer science) wikipedia , lookup
Object-oriented programming wikipedia , lookup
Reactive programming wikipedia , lookup
Relational model wikipedia , lookup
Program optimization wikipedia , lookup
Algorithm characterizations wikipedia , lookup
Go (programming language) wikipedia , lookup
Structured programming wikipedia , lookup
Coding theory wikipedia , lookup
K-nearest neighbors algorithm wikipedia , lookup
Error detection and correction wikipedia , lookup
CAL Actor Language wikipedia , lookup
Falcon (programming language) wikipedia , lookup
Control table wikipedia , lookup
One-pass compiler wikipedia , lookup
C Sharp syntax wikipedia , lookup
C Sharp (programming language) wikipedia , lookup
Expectation–maximization algorithm wikipedia , lookup
Corecursion wikipedia , lookup
Programming
Section 3
WHAT IS AN ALGORITHM?
An algorithm is a sequence of precise instructions for solving a
problem in a finite number of steps.
Properties/Characteristics:
Algorithms must:
be precise,
be unambiguous,
be logically sequenced,
give the correct solution an all cases, and
eventually end.
Algorithmic structure
Header
: Algorithm’s name or title
Declaration
: Brief description of algorithm and variables
used. i.e. A statement of purpose as well as
the initialization of variables
Body
: Sequence of steps
Terminator
: An end statement
ALGORITHMIC STRUCTURE
Problem:
Write an algorithm that prompts a student to enter his/her
name and age, accepts the name and age and then display a
welcoming message on the screen such as “hello Michael! You
are 16 years old!”
Write the algorithm identifying the header, declaration, body
and terminator.
ALGORITHMIC STRUCTURE
Algorithm Student data
This algorithm displays a student’s
name and age on the screen.
Start
Display “Enter your name:”
Accept Name
Display “Enter your age:”
Accept Age
Display “Hello”, Name
Display “You are”, Age, “years old”
Stop
{Header}
{declaration}
{Body}
{Terminator}
EXAMPLE
• Write an algorithm that will read the radius of a circle and
calculate and display its perimeter.
Input
Processing
radius
Accept radius
Calculate circumference
Store results in circumference
Display circumference
Step 1: start
Step 2: read radius
Step 3: circumference 2 * 3.14* radius
Step 4: write circumference
Step 5: stop
Output
circumference
EXAMPLE
• Write an algorithm that displays the area of a rectangle by
accepting length and width from the user.
Input
Processing
Output
length, width
Accept length, width
Calculate area
Store results in area
Display area
Area
Step 1: start
Step 2: read length, width
Step 3: area length * width
Step 4: write area
Step 5: stop
EXAMPLE
• Write an algorithm to read three numbers and find their
product.
Input
Three
numbers
(num1,
num2,num3)
Processing
Accept numbers
Calculate product
Store results in
product
Display product
Output
Product
Step 1: start
Step 2: read num1, num2, num3
Step 3: product num1*num2*num3
Step 4: write product
Step 5: stop
FLOWCHARTS VERSUS PSEUDOCODE
• Pseudocode is more concise, closely resembles programming
language
• Flowchart gives good view of the structure and flow of the
logic
• Beginners tend to follow the logic easier when using
flowcharts rather than pseudocode
• Longer, more complex solutions are better represented using
pseudocode.
FLOWCHARTS VERSUS PSEUDOCODE
• Usage is a matter of preference for experienced programmers
• Students should be asked to use both flowcharts as well as
pseudocode to represent algorithms
• Flowcharts must use special geometrical objects that
designate the basic steps of a program:
Flow of Control
Input/Output
Processing/
Assignment
Decision
Start/ Stop
PSEUDOCODE AND FLOWCHART
•
•
•
•
•
Start
Get num1, num2, num3
Average (num1 + num2 + num3)/3
Print Average
Stop
Start
Read num1,
num2, num3
Average
(num1+num2+num3)/3
Print
Average
Stop
Draw flowcharts for the following programs:
• Program to accept the price of an item and calculate its VAT at
15%.
start
read price
vat price *.15
write vat
stop
Example
• Program to accept money in US dollars and convert it to its equivalent
local currency.
start
read us
ec us *2.71
write ec
stop
Distinguish between variables and constants;
• Variable = the name identifies what the value
represents.
• Constant = A value (Alphabetical/numerical) that
never changes during processing.
(Eg. the value of PI)
•
Use appropriate data types
Data Types
Examples
String
“Hello”, “Carl” “New York” “Mary”
Character
a,e,i,o,f,h,j,k,h
Real or Floating point
2.3, 45.6, 36.3, 88.1, 3.5,
Boolean
Yes, No, True, False,
Integer/Whole numbers
1,4,988,99,88,66,
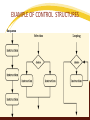
Control Structures
• That are commonly used in programming languages.
• Sequencing- Execute one single instruction, in a section of
program, after another.
• Selection- Choose, depending on a tested condition,
between two, or more pathways through a section of a
program.
• Repetition/Looping- Executing a single instruction, or group
of instructions, one or more times.
EXAMPLE OF CONTROL STRUCTURES
Sequence
SELECTION STRUCTURES
• IF … THEN … ELSE construct syntax:
• IF (expression) THEN
{Statements} executed only if condition is TRUE
ELSE
{Statements} executed only if condition is FALSE
ENDIF
• Only one group of statements could be executed each time
the program is executed.
SELECTION STRUCTURES
Get Mark
IF Mark >= 50 THEN
PRINT “ Well done”
ELSE
PRINT “Must do better”
ENDIF
Stop
• “Well done” will be printed
should the student’s mark
be 50 or greater.
• If the mark is less than 50
then the statement “Must
do better” would be
printed.
REPETITION STRUCTURES
• Repetition or Loop or Iteration structures allow statements to
be repeated a fixed number of times or until some condition
evaluates to false.
• There are three repetition constructs:
1.
FOR Loop
- counted loop
2.
REPEAT Loop
- conditional loop
3.
WHILE Loop
- conditional loop
The basic structure of the loop is:
• Initialise a variable to a star value (usually determines
whether or not the loop is executed)
• Test variable against condition
• Execute the body of the loop
• Update the value of the start variable
Loop Statement
There are two types of loop statements:
Indefinite: This refers to when you do not know beforehand how
many times to repeat the loop. (WHILE and REPEAT loops)
General Form of the WHILE-DO loop
WHILE (condition) Statement
Example.
Age = 16
WHILE (age <21) DO
BEGIN
Output "You cannot drink"
Age = age + 1
END
Output "The loop has ended"
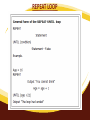
REPEAT LOOP
Definite
•
This refers to when you know beforehand how many times to
repeat the loop. (FOR loop)
Note:
i. The symbols := must
go together
ii. Variable must be in
order so it can be
counted.
iii. Variable begins with
start value.
iv. Loop variable is
increased every time
the loop goes around.
v. The loop will
terminate/end when the
counter reaches the
value of the final
expression
INITIALIZATION OF VARIABLES
• Variables that are used as counters or used to store totals
should always be assigned an initial value of 0 before they are
incremented.This is called initialization
Counters
• This is the process of counting the number of times a value is
entered or a statement is carried out. You can also allow your
counter to begin at 0 and then increment (increase
accordingly).
• E.g.
• Counter <--- 0
Counter <---- Counter + 1
• In the example above, counter is initially set at 0, which
means that every time the assignment statement is executed,
the value of the counter variable is increased by 1.
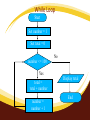
Draw flowcharts for the following
• .
Algorithm:
Set the number = 1
Set the total = 0
While (number <= 100)
total = total + number
number = number + 1
End While
Display total
While Loop
Start
Set number = 1
Set total = 0
No
number <= 100
Yes
total =
total + number
number =
number + 1
Display total
End
Use of relational operators:
The following relational operators are used:
Table 1 Relational Operators
Operator
Name
Symbol
Description
Equal
=
Returns true if both sides are equal.
Greater than
>
Returns true if the variable on the left is greater than the
variable on the right.
Less than
<
Returns true if the variable on the left is less than the variable
on the right.
Greater than or equal to
>=
Returns true if the variable on the left is greater than or equal
to the value of the variable on the right.
Less than or equal to
<=
Returns true if the variable on the left is less than or equal to
the value of the variable on the right.
Not equal to
<>
Returns true if both sides are not equal.
example
Table 2 truth table for relational operators
Operator Symbol
Example (Assume
True when
A = 20, B = 15)
False when
A and B are
different
Result
=
A=B
A and B are same
or equal
>
A>B
A is greater than A is not greater
B
than B
True
<
A<B
False
>=
A >= B
A is less than B A is not less than
B
A is greater than B is greater than
or equal to B
A
<=
A <= B
A is less than or
equal to B
False
<>
A <> B
A is not equal to A and B are same
B
or equal
B is less than A
False
True
True
Logical Operators
• The logical operators are used for Boolean
expressions. A Boolean expression can be in one
of two states: True or False. Depending on the
state of the expression.
• The three basic types of logical operators are:
NOT, AND, OR
NOT OPERATOR
• NOT is a unary operator — it is applied to only
one value and inverts it:
• ·
not true = false
• ·
not false = true
AND OPERATOR
• AND yields TRUE ONLY if both values are TRUE:
• ·
•·
•·
•·
TRUE and FALSE = FALSE
TRUE and TRUE = TRUE
FALSE and TRUE = FALSE
FALSE and FALSE - FALSE
OR OPERATOR
• OR yields TRUE if at least one value is TRUE:
• ·
•·
•·
•·
TRUE or TRUE = TRUE
TRUE or FALSE = TRUE
FALSE or TRUE = TRUE
FALSE or FALSE = FALSE
EXAMPLE
•
•
•
•
•
•
•
•
A = 10, B = 12, C = 14, D = 11
1. A = B (FALSE)
2. A > B (FALSE)
3. (A < C) AND (B < D) (FALSE)
4. (A>B) OR (A < 5 (FALSE)
120
22
)5. (D>A) AND (C > D) ( TRUE)
6. (A>B) OR ((A+B)<(A *B)) (TRUE) 10>12 (f) 0R 10+12<10*12
7. NOT (B>D) (TRUE)
Arithmetic Operations
Some arithmetic operations offered by Darwin.
Operation
Symbol
Example
Result
addition
+
101+27
128
subtraction
-
15-3
12
multiplication
*
5*3
15
division
/
6/2
3
test algorithms for correctness
We use a trace table which is one that is completed by
tracing the instruction in the algorithm with appropriate
data to arrive at solutions.
•
The column headings of a trace table record the
names of all the variables used in the algorithm.
•
The rows record the state of the variables after every
instruction execution.
Copy the following trace table. Complete the trace
table, given that the number 4 is the input
value for X.
Read X
For M = 1 to X do
Y=X–M
Z=5*Y–M
END
Print Z
What does the algorithm prints?
Z= 14,8,2,-4
The algorithm prints -4
2
3
4
3
2
1
0
14
2
-4
test algorithms for correctness;
63*2
18
6*3
2+1
3
3+0
3
1-1
0
-1
0-1
use the top-down design approach to
problem solving.
• Top-Down Design Approach or Modular Programming as it is
sometimes called involves breaking a problem into a set of
smaller problems, called sub-problems or modules, followed
by breaking each sub-program into a set of tasks, then
breaking each task into a set of actions. This is called stepwise
refinement
• General Rule in modular programming is that a module
should be comprised of statements that contribute to a single,
specific task.
.
Steps in Modularization:
1. Define the problem
2. From the processing section, identify the tasks that will
determine the modules that will make up the program. Each
non-trivial task should constitute a module.
3. Construct a hierarchy chart showing the modules and the
relationship between them.
4. Formulate the algorithm for the main module in either
pseudocode or flowchart.
5. Develop sub-algorithms for each module.
6. Test the algorithm for correctness.
Advantages of the Top-Down Design Method:
• 1. It makes the problem solution more manageable.
It is easier to comprehend the solution of a smaller
and less complicated problem that to grasp the
solution of a large and complex problem.
•
2. It is easier to test segments of solutions, rather
than the entire solution at once.
•
3. A simplified solution takes less time to develop
and will be more readable.
•
4. The program will be easier to maintain.
A Hierarchy chart
• or structure chart is a tree-like structure that shows visually
the relationships between the modules of a program
EXAMPLE 1.1:
Given a list of students test scores, find the highest and
lowest score as well as the average score.
Four sub-problems can be identified here:
1. Sub-problem 1: read list of test scores
2. Sub-problem 2: find_the_highest_score
3. Sub-problem 3: find_the_lowest_score
4. Sub-problem 4: find_the_average
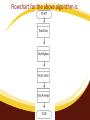
A Hierarchy chart
Flowchart for the above algorithm is:
distinguish between low-level and high-level
programming languages;
• Low level languages- These are languages which
are machine dependent; that is, when a code is
written on a particular machine, it can only be
understood by that machine.
• High level languages- These are languages that
are machine independent; that is, when a code
is written on a particular machine, it is not
limited to execution on that machine only but
can also run on other similar machines.
distinguish among the differe
generations of programming languages
First Generation Language- These are also called
machine languages and are characterized by ones
and zeros, which make up a binary code. A sample
instruction might be 100111000 01100110
Second-generation language- These are also called
assembly languages and are characterized by
abbreviated words, called mnemonics. A sample code
might be ‘Add 12,8’
Cont’d
Third- generation Languages- These are designed
so that it is easier for the programmer to
understand. A compile converts the statements of
a specific language into machine language.
• Fourth generation language (4Gls)- These are designed
to be closer to natural language than a 3GL. Languages
for accessing databases are often described as 4GLs.
*A sample instruction might be EXTRACT ALL CUSTOMERS
WHERE 'PREVIOUS PURCHASES' TOTAL MORE THAN
$1000.
• Fifth Generation- Programming that uses
a visual or graphical development
interface to create the source code. They
are often described as very high level
language.
To get the object code from the source code,
• We use a translator programme. Three types of such
programmes are interpreters, compilers and
assemblers.
• Interpreter- Translates the source code, line by line.
If an error is detected, translation is stopped.
• Compiler-Translates all instructions at once and
produces a stand-alone object code that can be
executed.
• Assembler-Translates mnemonic-type instructions
[Assembly Language] to machine code.
List the sequence of steps associated with
implementing a program;
•
•
•
•
•
Creating source code
Compiling
Linking
Executing
Maintaining.
Difference between
• Sources codes are programmes written in high-level
or assembly-level language
• Object codes are machine codes which have been
converted to machine language by the compile
• Compilers-A compiler is a computer programme
which translates source codes to machine
language. It does so, first, by converting the
codes of the high-level language and storing it as
object codes.
•
Source Code------Compiler------Object Code
explain commonly used terms and
concepts in programming;
• Logic errors occur when the programmer makes mistakes in the
sequence of the program statements such using the wrong formula
or function.
• Syntax errors occur when a mistake is made in the programming
language rules . For example if a keyword such as input or print is
spelt incorrectly or an endif was left out.
• Run-time errors occur as the program compiles or runs. These
errors are usually due to unexpected events such as division by zero
or lack of memory for the computer to manipulate the data or a
loop with no end.
• Example: for x = 1 to 3
• Debugging is the process of finding errors in the source code
(detection), understanding why they occurred (diagnosis) and
correcting them.
• Testing-As you complete your program, you must ensure that
it works for any correct input data that the user gives it. The
testing phase is to detect errors or problems in the program.
• Test data: the values that are used to test or check the
correctness of the program. The test data should include a
wide range of sample data including extreme values and
inputs that are not valid.
Executing the program
• If you have translated the program to its object code without
errors, you can now execute the program and see the results.
The final two terms commonly used with program execution
are:
• Program loading: Copying of a programme from the hard disk
of the computer to memory so it can be used.
• Linking: Combining various parts of a programme to produce
a single executable file.
•
Declare variables
• It is important to declare our variables when writing out
programmes because they occupy space in memory that we
can use to assign values and the compiler needs to know, in
advance, the type of data that will be stored in it. These types
include:
• Integer - stores whole numbers
• Real - stores fractional numbers in the decimal format
• Character - stores a single character such as a letter
• String - stores a collection of characters
Declare constants;
The assignment statement
• The assignment statement is used to store a value in a variable
after the operation (i.e. +,-,*, or /) has been performed.
• VARIABLE = Expression (i.e. what is to be calculated)
• Examples of assignment statements are:
• 1. NUM1 = 5 (i.e. Store the value 5 in the variable NUM1)
• 2. SUM = NUM1 + 50 (i.e. Add 50 to the value stored in NUM1,
then store the total in the variable name sum)
• 3. Product = NUM1*SUM(i.e. Multiply the content of NUM1 by
the content of SUM)
The input statement
• The input statement is used to fetch data from some external
source and store the data in a variable. The data stored in the
variable can then be manipulated by the pseudocode.
• Examples of input statement used by pseudocode developers
are:
• Read
• Input
• Fetch
• Get
Pseudocode example one
• Write a pseudocode to read two numbers into variable A and B.
• Solution
Read A
Read B
Pseudocode example two
• Write a pseudocode to read the name and score for three
persons.
• For this question, we need to store six pieces of data, three
names and three test grades, respectively. Hence, six variables
are needed. Our variable will be called:
• NAME1, NAME2, NAME3, GRADE1, GRADE2 and GRADE3.
Pascal
•
•
•
•
•
•
•
Writeln (pronounced as "write-line") statement displays the
data on screen and then moves the cursor to the next new
line. while Write statement does not.
examples of Writeln
Write
Writeln('a');
Write('Macintosh ');
Writeln('Hello');
Write('Computer.');
Writeln('How are you ?');
Write('Hello');
Writeln;
Writeln('a', 'b', 'c');
Read/Readln
• Readln statement will cause the computer to advance (move)
the cursor to the beginning of the next line after execution
while read statement will not.
•
•
•
•
Example of Readln
Readln(a,b);
Readln(c,d);
Readln(e,f);
Read
Read;
Read;
ARRAY
• An Array is a powerful data structure that stores variable data
having the same data type.
DECLARE an Array
• Var
• myArray : Array[1..20] of Integer;
• <arrayName> : Array[n..m] of <Data Type>;
Assigning values to array?
• To assign values to a particular integer of an array, we do it
like this:
• myArray[5] := 10; myArray[1] := 25;
•
<arrayName>[index] := <relevant data>
Reading array
• Reading a value from an array is done as follows:
• Var
myVar : Integer;
myArray : Array[1..5] of Integer;
Begin
myArray[2] := 25;
myVar := myArray[2];
End.
• Just like ordinary variables, arrays should be initialised,
otherwise scrap data will remain stored in them. If we want to
intialise 2 whole 20-sized integer and boolean arrays to 0 and
false respectively, we do it like this:
Var
i : Integer;
myIntArray : Array[1..20] of Integer;
myBoolArray : Array[1..20] of Boolean;
Begin
For i := 1 to 20 do
Begin
myIntArray[i] := 0;
myBoolArray[i] := false;
End;
End.
Introducing User-Defined Data Types
•
Built-in data types are the ones we used lately, such
as Integer, Boolean and String. Now we will learn how to
specify our own customised data types and this is just how it
is done:
Type
<myDataType> = <particularDataType>;