Download Section 6.4

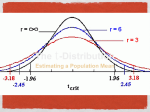
Section 6.4
Distribution of a
Sample Mean
Statistics: Unlocking the Power of Data
Lock5
Outline
 Standard error for a sample mean
 CLT for sample means
 t-distribution
 Distribution of sample mean
Statistics: Unlocking the Power of Data
Lock5
SE for 𝒙
The standard error for 𝑥 is
𝜎
SE =
𝑛
 The larger the sample size, the smaller the SE
Statistics: Unlocking the Power of Data
Lock5
Standard Deviation
The standard deviation of the
population is
a) 
b) s
c)
𝜎
𝑛
Statistics: Unlocking the Power of Data
Lock5
Standard Deviation
The standard deviation of the sample is
a) 
b) s
c)
𝜎
𝑛
Statistics: Unlocking the Power of Data
Lock5
Standard Deviation
The standard deviation of the sample
mean is
a) 
b) s
c)
𝜎
𝑛
The standard error is
the standard deviation
of the statistic.
Statistics: Unlocking the Power of Data
Lock5
Olympic Marathon Times
 78 runners finished the 2008 Olympic Men’s
Marathon. The averaging finishing time was 
= 141 minutes, and the standard deviation of
finishing times was  = 7.4 minutes.
 If we were to take random samples of 10 men
finishing the 2008 Olympic marathon, what
would the standard error of 𝑥 be?
𝑆𝐸 =
𝜎
𝑛
Statistics: Unlocking the Power of Data
=
7.4
10
= 2.3
Lock5
Olympic Marathon Times
Statistics: Unlocking the Power of Data
Lock5
CLT for a Mean
Population
8
3.0
1.5
0 1 2
10
x
n = 30
2.0
3.0
2
3
4
5
1.5
2.0
2.5
3.0
25
1
0 2 4
Statistics: Unlocking the Power of Data
1.0
0 10
Frequency
0
n = 50
3 4 5 6
8
6
4
4
0
2
Frequency
0
Distribution of
Sample Means
0.0
n = 10
Frequency
Distribution of
Sample Data
6 8
12
1.4
1.8
2.2
2.6
Lock5
CLT for 𝒙
If n is sufficiently large:
𝜎
𝑥 ~ 𝑁 𝜇,
𝑛
 A normal distribution is usually a good
approximation as long as n ≥ 30
 Smaller sample sizes may be sufficient for
symmetric distributions, and 30 may not be
sufficient for very skewed distributions or
distributions with high outliers
Statistics: Unlocking the Power of Data
Lock5
Math SAT Scores
 For the class of 2010, the average score on the
mathematics portion of the SAT is  = 516 with
a standard deviation of  = 116.
 If we were to take random samples of 50
students taking the SAT, what would the
distribution of 𝑥 be?
𝜎
116
𝑆𝐸 =
=
= 16.4
𝑛
50
𝑥 ~ 𝑁(516, 16.4)
Statistics: Unlocking the Power of Data
Lock5
Standard Error
SE =
𝜎
𝑛
• Usually, we don’t know the population
standard deviation , so estimate it with
the sample standard deviation, s
SE 
Statistics: Unlocking the Power of Data
𝑠
𝑛
Lock5
t-distribution
• Replacing  with s changes the
distribution of the standardized test
statistic from normal to t
• The t distribution is very similar to the
standard normal, but with slightly fatter
tails to reflect this added uncertainty
Statistics: Unlocking the Power of Data
Lock5
Degrees of Freedom
• The t-distribution is characterized by its
degrees of freedom (df)
• Degrees of freedom are calculated based
on the sample size
• The higher the degrees of freedom, the
closer the t-distribution is to the
standard normal
Statistics: Unlocking the Power of Data
Lock5
t-distribution
Statistics: Unlocking the Power of Data
Lock5
Aside: William Sealy Gosset
Statistics: Unlocking the Power of Data
Lock5
t-distribution
• If a population with mean µ0 is approximately
normal or if n is large (n ≥ 30), the standardized
statistic for a mean using the sample s follows a
t-distribution with n – 1 degrees of freedom:
𝑥 − 𝜇0
~𝑡𝑛−1
𝑠
𝑛
Statistics: Unlocking the Power of Data
Lock5
t-distribution
Which of the following properties is/are
necessary for 𝑡 =
a)
b)
c)
d)
e)
𝑥−𝜇0
𝑠
to have a t-distribution?
𝑛
the population is normally distributed
the sample size is large To use the t-distribution,
the null hypothesis is true either n has to be large or
the population has to be
a or b
normally distributed. If these
conditions are met, then t
d and c
has a t-distribution when the
Statistics: Unlocking the Power of Data
null hypothesis is true.
Lock5
Normality Assumption
• Using the t-distribution requires that the data
comes from a normal distribution
• Note: this assumption is about the population data,
not the distribution of the statistic
• For large sample sizes we do not need to worry
about this, because s will be a very good estimate of
, and t will be very close to N(0,1)
• For small sample sizes (n < 30), we can only use the
t-distribution if the distribution of the data is
approximately normal
Statistics: Unlocking the Power of Data
Lock5
Normality Assumption
• One small problem: for small sample sizes, it is very
hard to tell if the data actually comes from a normal
distribution!
Population
0
2
4
6
Sample Data, n = 10
8
10
0
2
4
6
8
10 0
1
2
3
4
5
6 0.5
1.5
2.5
3.5
x
-4
-2
0
2
4
-2.0
-1.0
0.0
Statistics: Unlocking the Power of Data
1.0
-0.5
0.5 1.0 1.5 2.0
-2
-1
0
1
Lock5
Small Samples
• If sample sizes are small, only use the t-
distribution if the data look reasonably
symmetric and do not have any extreme
outliers.
• Even then, remember that it is just an
approximation!
• In practice/life, if sample sizes are small, you
should just use simulation methods
(bootstrapping and randomization)
Statistics: Unlocking the Power of Data
Lock5