Download MATH 092 Topic Guide

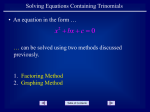
The following is a list of the topics with brief descriptions covered in MATH 092. This
list covers the breadth but not the depth of the content. Thus the provided examples are
not a comprehensive representation of the type of content that may appear on the challenge
exam. It is not the purpose of this guide to be studied, but rather to help the student to
find study materials.
1. Prealgebra
(a) Integers
Computing with integers; including addition, subtraction, multiplication and division. Example content:
−4 · −12 = 48
− 4 + (−3) = −7.
and
(b) Rational Numbers
Computing with rational numbers; including addition, subtraction, multiplication
and division. Example content:
1 2
1
1 3
÷ = · = .
2 2
2 3
3
Introduce complex fractions and equivalent form of division:
1
2 = 1 ÷ 3 = 1 · 2 = 1.
3
2 2
2 3
3
2
(c) Prime Factoring
Review definition of prime numbers and how to write a number in its prime
factored form. Review factor tree. Example content:
12
4
2
.
3
2
(d) Simplifying Expressions
Simplifying expressions using the correct order of operations. Example content:
−2 · 32 + 4(7 − 5).
(e) Translating from word to number expressions.
Review key words in translating words to number expressions. Emphasis on words
such as sum, difference, product, quotient, is, of, etc. Example content:
1
Forty percent of eighty people is thirty-two people.
(f) Reading Graphs
Interpret information based on line, bar, or circle graphs.
2. Equations in One Variable
(a) Combining like terms. (review)
Review definition of variable. Combine similar terms in expressions. Example
content:
2ab + 3x − 5ab.
(b) Solving equations with 2 - 3 steps. (review)
Solve equations with two operations, including parenthesis. Example content:
2(x + 3) = 10.
(c) Solving and graphing basic linear inequalities. (review)
Review algebraic rules for manipulating inequalities; in particular, multiplication
and division by negative values. Equations should require at most 3 steps to
solve and should not have a variable on both sides of the inequality. Compound
inequalities should be reviewed as well. Example content:
2 < 2x − 3 < 5.
(d) Solving equations containing fractions.
Solving equations with fractions as solutions. Solving equations with fractions as
coefficients. Discuss how to use the least common denominator (lcd) to simplify
the equation. Example content:
1
3
5
x+
= .
7
14
28
(e) Solving equations with parenthesis and variables on both sides of the equality.
Example content:
2(x + 5) = −3x + 12.
(f) Solving formulas for a specified variable.
Extra time should be spent on this topic as it is a critical skill, yet often very
difficult for students. Arbitrary equations may be used but common formula (area
of a circle, equation of a line, ideal gas law) should also be represented. Example
content:
2
Solve the following equation for a:
bx
= y.
a
(g) Word problems.
Basic word problems including but not limited to distance = rate time (DRT).
Problems should be very simple at this stage. Example content:
If Mary is traveling at 45mph for 3 hours, how far has she gone?
3. Graphing Linear Equations
(a) Plotting ordered pairs. (review)
Review the Cartesian coordinate system. Example content:
Plot (2, −3).
(b) Graphing linear equations by plotting points.
The concept of the graph of a linear equation as the set of solutions of a linear
equation should be introduced and emphasized. Use of the t-chart method (or
similar) to plot points of a a linear equation should be introduced. Example
content:
Graph y = 2x − 3 by plotting points.
(c) Slopes of Lines
Definition and formula for slopes of lines. Discuss a slope of zero and undefined
slope. Example content:
Find the slope between (−4, 5) and (−4, 8).
(d) Finding and graphing equations of lines.
Find equations of lines in point-slope, standard and slope-intercept form, and
graph them. Example content:
Write the equation of the line that passes through the vertex and (4, 5),
in slope-intercept form. Then graph.
(e) Equations of horizontal and vertical lines.
General form of horizontal and vertical lines. Graph horizontal and vertical lines.
Recognize the slope of the lines. Example content:
Identify if the equation is of a horizontal or vertical line. Then graph
y = 4.
(f) Equations and graphs of parallel and perpendicular lines. (optional)
Discuss the relationship between the slopes of parallel and perpendicular lines.
Example content:
2
Find the equation of a line perpendicular to y = x − 4 that passes
3
through the origin.
3
4. Systems of Equations
(a) Introduction to systems of linear equations in two variables.
Define a system of equations. Discuss consistent and inconsistent systems.
(b) Solving systems by graphing.
Example content:
Solve the system of equations by graphing:
y = 3x + 5
.
y = 2x − 1
(c) Solving systems by substitution.
Discuss substitution method. Solve systems that are ready for substitution and
others where rearranging one equation, must take place first. Discuss consistent
and inconsistent systems. Example content:
Solve the system of equations by substitution:
4x + 3y = 8
.
2x + y = −1
(d) Solving systems by elimination.
Discuss elimination method. Solve systems that are ready for elimination and
others where a multiplication by a constant, must occur first. Example content:
Solve the system of equations by elimination:
4x + 3y = 9
.
−2x + y = −1
(e) Applications of systems to basic word problems.
Use systems of equation to solve word problems involving money, DRT, etc. Example content:
Fred has quarters and nickels whose combined value is $0.55. The sum
of the number of quarters and nickels is 3. How many of each does Fred
have?
5. Exponents
(a) Using integer exponents; general rules of exponents. (review)
Use the product, quotient, power, zero, and negative exponent rules. Example
content:
x3
x2
or
4
1
.
x−3
(b) Multiplying and dividing exponential expressions. (single term)
Use general rules of exponents in order to help simplify expressions. Example
content:
(2x2 y)3
.
x−1 y 2
(c) Using scientific notation.
Multiply and divide numbers in scientific notation. Example content:
3.8 × 108
2.7 × 1012 .
6. Polynomials
(a) Definition of a polynomial in one variable. (review)
Give the technical definition of a polynomial and using the definition to classify
whether an expression is a polynomial or not. If the given expression is a polynomial, classify by the degree and number of terms. Discuss the standard form of a
polynomial. Example content:
Is the expression
√
3x2 + 2 x,
a polynomial? If so, give its classification.
(b) Adding, subtracting, and multiplying polynomials.
Perform addition and subtraction with polynomials of varying powers. Review
how to multiply a monomial by a polynomial. Also multiply binomials by binomials and binomials by polynomials. Discuss the degree of the resulting polynomial
based on the operation performed. Example content:
(2x2 + 3x − 7)(5x2 − 2x + 1).
(c) Dividing a polynomial by a monomial.
Apply rules of exponents in order to divide a polynomial by a monomial where
the result is another polynomial. Example content:
3x2 + 2x
.
2x
7. Factoring Polynomials
(a) Factoring by the greatest common factor (GCF).
Factoring out the greatest common factor when it is a number, variable or combination. Example content:
Factor
2x2 + 4x − 6x3 .
5
(b) Factoring by grouping.
Factoring a four-term polynomial using grouping. Example content:
Factor
2x2 + 6x + x2 + 3x.
(c) Factoring general trinomials.
Factor quadratic trinomials where the leading coefficient is 1. Example content:
Factor
x2 + 7x + 10.
(d) Factoring perfect squares.
Discuss the formula a2 + 2ab + b2 = (a + b)2 , for factoring a trinomial that is a
perfect square. Example content:
Factor
x2 + 10x + 25.
(e) Factoring difference of squares.
Discuss the formula a2 − b2 = (a − b)(a + b), for factoring the difference of two
squares. Apply to simple examples where the squared term is obvious. Example
content:
Factor
x2 − 4.
8. Quadratic Equations
(a) Solve a quadratic equation by factoring.
Discuss the zero product property. Apply all the different types of factoring in
order to solve quadratic equations. Example content:
Solve
x2 + 10x + 25 = 0,
by factoring.
(b) Solve a quadratic equation using the square root property.
Define a square root. Discuss how to solve a quadratic equation by taking the
square root. Example content:
Solve
(x + 2)2 = 16,
using the square root property.
(c) Solve a monic quadratic equation by completing the square where b/2 is an integer.
Discuss the process for completing the square and discuss perfect square trinomials. Example content:
6
Solve
x2 + 8x + 3 = 0,
by completing the square.
(d) Solve a quadratic equation using the quadratic formula.
Present the quadratic formula without derivation. Use the quadratic formula to
solve quadratic equations. Discuss the discriminant and its relation to the number
of solutions. Example content:
Solve
x2 + 5x = 3,
using the quadratic formula.
(e) Introduction to basic graphs of quadratics.
Discuss the parent graph y = x2 and the properties and terminology of a parabola.
Graph basic quadratics by plotting points. Example content:
Graph
y = x2 − 3,
by plotting points. Identify the vertex and any zeros.
9. Rational Equations
(a) Introduction to rational expressions.
Define a rational expression. Introduce terminology for classification such as
proper and improper rationals.
(b) Simplify rational expressions.
Using a variety of factoring techniques in order to simplify rational expressions.
Example content:
Simplify
x2 − 4
.
x2 + 4x + 4
(c) Adding, subtracting, multiplying and dividing rational expressions.
Example content:
x2 − 4
x+3
÷
.
2
x + 4x + 4 x + 2
(d) Simplifying complex fractions.
Discuss the two methods to simplify: multiply both the numerator and the denominator by the gcd of both or convert to single fractions in both numerator
and denominator and then "flip and multiply".
7
Simplify
x+2
x+3 .
x+5
x+2
(e) Solving rational equations.
Utilize various methods to solve rational equations with both constant, linear,
and quadratic forms. Discuss valid and invalid solutions, emphasizing to check
their solutions in the original equation. Example content:
Solve and check your solution(s).
5
x
2
+
= 2
.
x+2 x+3
x + 5x + 6
10. Radicals
(a) Rules of radicals.
Explain the rules for manipulating radicals including cancellation rules for both
even and odd powers. Example content:
√
n
xn
=
|x| for n even,
x for n odd.
(b) Simplifying radical expressions.
Use prime factorization and cancellation rules to simplify radical expressions.
Example content:
Simplify:
√
50x3 .
(c) Arithmetic on radical expressions.
Add, subtract and multiply radical expressions. Primarily square roots and some
cube roots. Example content:
Simplify:
√
15 +
√
75.
(d) Rationalizing denominators.
Rationalize single term denominators.
Rationalize and simplify:
3
√ .
6
(e) Rules of exponents for rational exponents.
Review rules for exponents now allowing for rational exponents: x1/n and xm/n .
Focus on simple problems with the application of a single rule. Example content:
2
83
or
8
x2
1
x3
.
(f) Right triangle problems and the Pythagorean Theorem.
Discuss the Pythagorean theorem and related terminology. Using right triangles,
find missing sides. Example content:
If a right triangle has a hypotenuse of length 10 and one side of length
6, what is the length of the other side?
(g) Solving radical equations. (optional)
Solve simple radical equations. Emphasize checking the answer by substituting
into the original equation. Discuss valid and invalid solutions as well as equations
with no real solutions. Example content:
Solve
√
x + 5 = 21
√
x + 5 = 4.
and
11. Functions
(a) Function definition and notation.
Define functions, vertical line test, standard notation, and other terminology.
Emphasize y as representing the output of the function as opposed to the function
itself in f (x) = y.
(b) Evaluating functions.
Reiterate independent and dependent variable terminology. Relate back to points
as solutions and again emphasize y as the output and f (x) as the function. Example content:
If f (x) = 2x + 5, evaluate the function for x = 2.
(c) Graphing linear and nonlinear functions.
Graph linear functions by any method. Graph nonlinear functions by plotting
points. Example content:
Graph y = |x + 1|.
(d) Identifying domain and range of functions.
Discuss the definitions of domain and range. Identify the domain and range of a
function looking at a graph. Identify the domain and range of simple functions
with inequality solutions. Example content:
What is the domain and range of:
f (x) =
9
√
x.