Download CS-240 Data Structures

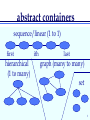
abstract containers
sequence/linear (1 to 1)
first
hierarchical
(1 to many)
ith
last
graph (many to many)
set
1
trees
 hierarchical
organization
each item has 1 predecessor and 0 or more
successors
 one item (root) has 0 predecessors

 general
tree - no limit on number of
successors
 binary tree - 2 successors (left and right)
 binary search tree is one use of a binary
tree data structure (will deal with later)
2
tree terminology
There is a unique
path from the root
to each node.
Root is a level 0, child
is at level(parent) + 1.
Depth/height of a tree
is the length of the
longest path.
level
0
1
2
3
4
3
trees are recursive
Each node is the root
of a subtree.
Many tree processing
algorithms are best
written recursively.
4
binary tree

Each node has two successors



one called the left child
one called the right child
left child and/or right child may be empty
A binary tree is either
- empty or
- consists of a root and two
binary trees, one called
the left subtree and one
called the right subtree
5
binary tree density (shape)

a binary tree of depth n is complete iff

levels 1 .. n have all possible nodes filled-in





level 1:
level 2:
level 3:
level n:
1
2
4
?
nodes at level n occupy the leftmost positions
max nodes level at n: 2n-1
 max nodes in binary tree of depth n: 2n-1
 depth of binary tree with k nodes: >floor[log2 k]
 depth of binary tree with k nodes: <ceil[log2 k]
 longest path is O(log2 k)

6
representing a binary tree
have to store items and relationships (predecessor
and successors information)
 array representation

each item has a position number (0 .. n-1)
 use the position number as an array index




O(1) access to parent and children of item at position i
wastes space unless binary tree is complete
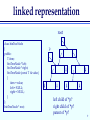
linked representation

each item stored in a node which contains:



the item
a pointer to the left subtree
a pointer to the right subtree
7
array representation

each item has a position number




root is at position 0
root's left child is at position 1
root's right child is at position 2
in general:



left child of i is at 2i + 1
right child of i is at 2i + 2
parent of i is at (i-1)/2
0
1
3
2
4
5
6
- - - - - - 0 1 2 3 4 5 6
0
1
2
6
13
works well if n is known in advance and there are no "missing" nodes
8
linked representation
root
class binTreeNode
{
public:
T item;
binTreeNode * left;
binTreeNode * right;
binTreeNode (const T & value)
{
item = value;
left = NULL;
right = NULL;
}
};
binTreeNode * root;
p
left child of *p?
right child of *p?
parent of *p?
9
why is a binary tree so useful?
 for
storing a collection of values that
has a binary hierarchical organization
arithmetic expressions
 boolean logic expressions
 Morse or Huffman code trees

 data
structure for a binary search tree
 general tree can be stored using a
binary tree data structure
10
an expression tree
an arithmetic
expression consists of
an operator and two
operands (either of
which may be an
arithmetic expression)
 some simplifications



only binary operators
(+, *, /, -)
only single digit, nonnegative integer
operands
*
-
5
+
2
6
1
operands are stored in leaf nodes
operators are stored in branch nodes
11
traversing a binary tree

what does it mean to traverse a container?


many operations on a collection of items
involve traversing the container in which they
are stored



"visit" each item once in some order
displaying all items
making a copy of a container
linear collections (usually) traversed from first
to last

last to first is an alternative traversal order
12
binary tree traversals
 order
in which to "visit" the items?
 some common orders - visit an item
before its children (preorder)
 after its children (postorder)
 between its children (inorder)
 level by level (level order)

 by
convention go left before right
13
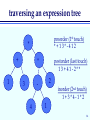
traversing an expression tree
preorder (1st touch)
*+13*-412
*
+
1
*
3
postorder (last touch)
13+41-2**
2
4
inorder (2nd touch)
1+3*4-1*2
1
14
expression tree traversal
traverse (ExprTree) {
if (root of ExprTree holds a digit) //is a leaf node
visit (root);
else // root holds an operand
{
visit (root)
traverse (ExprTree's left subtree)
traverse (ExprTree's right subtree)
}
}
15
expression tree operations

use "recursive partners"

allow recursive calls to deal with a subtree (identifed
by a pointer to its root node)
build uses a preorder traversal
 copy uses a preorder traversal
 postfix uses a postorder traversal
 clear uses a postorder traversal
 what kind of traversal does infix need?
 what kind of traversal does evaluate need?

16
Associative Containers
fast searching
17
STL Containers

Sequence containers




vector
list
deque
Adapters

Associative containers




stack
 queue
 priority_queue
set
map
multiset
multimap

unique keys non unique keys
keys only
key, value pairs
set
multiset
map
multimap
18
map containers

allow storing a collection of items each of which
has a key which uniquely identifies it




student records (social security number)
books in a library (ISBN)
identifiers appearing in a function (name)
has operations to



insert an item (key-value pair)
delete the item with a given key
retrieve the item with a given key
operations based on value, not position
 searching for a key is the critical operation

19
some possible data structures

array (or STL vector)



unordered
ordered by keys
linked list (or STL list)


unordered
ordered by keys
binary search tree
 balanced search trees
 hash table

20
comparative performance
data structure
Retrieve Insert Delete
unordered array
O(n)
O(1)
O(n)
ordered array
O(log2n) O(n)
O(n)
unordered
linked list
O(n)
O(1)
O(n)
ordered
linked list
O(n)
O(n)
O(n)
search trees and hash table both have better performance
21
binary search tree
each item is stored in a node of a binary tree
 each node is the root of a binary tree with the
BST property




all items stored in its left subtree have smaller key
values
all items stored in its right subtree have larger key
values
May be lop-sided. Insertion order matters.
22
the BSTree<TE, KF> class
 BSTreeNode
has same structure as
binary tree nodes
 elements stored in a BSTree are a keyvalue pair

must be a class (or a struct) which has



a data member for the value
a data member for the key
a method with the signature: KT key( ) const;
where KT is the type of the key
23
an example
struct treeItem
{
int id;
// key
string data;
// value
int key( ) const
{
return id;
}
};
BSTree<treeItem, int> myBSTree;
24
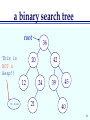
a binary search tree
root
This is
NOT a
Heap!!
20
12
No node
36
42
24
21
39
45
40
25
traversing a binary search tree
 can
use any of the binary tree traversal
orders – preorder, inorder, postorder

base case is reaching an empty tree
 inorder
traversal visits the elements in
order of their key values
 how would you visit the elements in
descending order of key values?
26
Recursive BST Search Algorithm
void search (bstree, searchKey)
{
if (bstree is empty)
//base case: item not found. Take needed action
else if (key in bstree's root == search Key)
// base case: item found. Process it.
else if (searchKey < key in bstree's root )
search (leftSubtree, searchKey);
else
search (rightSubtree, searchKey);
}
27
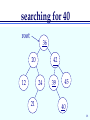
searching for 40
root
36
20
12
42
24
21
39
45
40
28
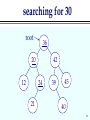
searching for 30
root
36
20
12
42
24
21
39
45
40
29
Recursive BST Insertion
 Similar
to BST search:
Insert_aux (nodeptr & subtree, &item)
If (subtree.root.empty( ) ) subtree.root=item
Else if (item < subtree.root)
Insert_aux (subtree.left, item) // try insert on left
Else if (item > subtree.root)
Insert_aux (subtree.left, item) // try insert on right
Else already in tree
 Just
keep moving down the tree
30
deletion cases
 item

to be deleted is in a leaf node
pointer to its node (in parent) must be
changed to NULL
 item
to be deleted is in a node with one
empty subtree

pointer to its node (in parent) must be
changed to the non-empty subtree
 item
to be deleted is in a node with two
non-empty subtrees
31
the easy cases
36
Just prune
it
20
12
42
24
21
Just set its
parent (42) to
skip this node
39
45
40
32
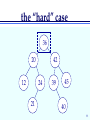
the “hard” case
36
20
12
42
24
21
39
45
40
33
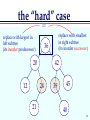
the “hard” case
or
replace with largest in
left subtree
(its inorder predecessor)
36
20
12
42
24
21
replace with smallest
in right subtree
(its inorder successor)
39
45
40
34
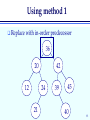
Using method 1
 Replace
with in-order predecessor
36
20
12
42
24
21
39
45
40
35
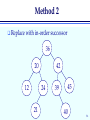
Method 2
 Replace
with in-order successor
36
20
12
42
24
21
39
45
40
36
big O of BST operations
 measured
by length of the search path
depends on the height of the BST
 height determined by order of insertion

 height
of a BST containing n items is
minimum: floor (log2 n)
 maximum: n - 1
 average: ?

37
faster searching
 "balanced"
search trees guarantee O(log2 n)
search path by controlling height of the
search tree
AVL tree
 2-3-4 tree
 red-black tree (used by STL associative
container classes)

 hash
table allows for O(1) search
performance

search time does not increase as n increases
38