* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Hunting oscillation wikipedia , lookup
Fictitious force wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Jerk (physics) wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Equations of motion wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Center of mass wikipedia , lookup
Seismometer wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hooke's law wikipedia , lookup
Classical central-force problem wikipedia , lookup
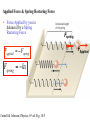
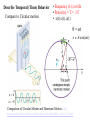
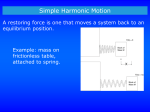
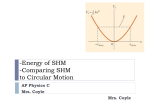
Today: Tue Oct 27 • Hooke’s Law • Assign 10 Friday – Use examples • Periodic Motion • Mass-Spring System Fapplied = kx ω spring = k m f spring 1 = 2π Note: T, f, ω are Independent k m Tspring m = 2π k of Amplitude! Each Red dot represents a 1kg mass on a massless turntable. The blue dot is 2kg. The inner circle has a radius half that of the outer circle. If the masses start in Configuration A and move to Configuration B while the turntable is spinning, how does the final angular speed of the turntable compare to the initial? (assume no external torque) (A) (B) 1. Greater 2. Smaller 3. Same LINITIAL= LFINAL Moment of Inertia stays same IA = (1kg)R2 +(1kg)R2 + (2kg)(½R)2 IB = (2kg)R2 +(1kg)(½R)2 + (1kg)(½R)2 IAωA = IB ωB IA = IB ; ωA = ωB A wheel of radius 0.30m rolls without slipping 15m along the sidewalk. How many revolutions did the the wheel undergo? (1) 0.72 rev (5) 15 rev (2) 6.2 rev (6) 50 rev (3) 8.0 rev Rolling w/o slipping x=rθ 15 m =0.3 θ θ = 50 rad 50 rad (1 rev/2π rad) = 7.96 rev (4) 9.7 rev Or Circumference = 2π r = 1.885m Distance/Circumference = # rev 15m/ 1.885 m = 7.96 rev Carousel Example • Playground carousel • As people redistribute, moment of inertia changes • As moment of inertia changes, angular speed changes A solid cylinder and a hoop roll down an incline. Both are the same mass and radius. Which reaches the bottom of the incline first? 1. The cylinder 2. The hoop 3. Both at same time "An object's moment of inertia determines how much it resists rotational motion. The cylinder has a smaller moment of inertia, so it’s easier “to get going”. Less energy goes into rolling the cylinder, so it has more translational kinetic energy at the bottom. Turns out that mass and radius don’t matter – solid cylinders will always beat hoops. Rolling Racers: four objects with same mass are placed on a ramp and left to roll without slipping. Starting from rest, which one is traveling the ramp length faster? 1. Spherical shell (I=2/3 MR2) 2. Solid sphere (I=2/5 MR2) 3. Hollow cylinder (I=MR2) 4. Solid cylinder (I=1/2 MR2) The solid sphere has a smaller moment of inertia, so it’s easier “to get going”. https://www.youtube.com/watch?v=b44WbCS9xnc What are the units for the spring constant, k? 1. N 2. m/N 3. N*m 4. N/m 5. kg*m 6. kg*N F k= x Repetitive Motion • Examples? • central force (circular motion) • restoring force (back and forth) • Oscillations • How can we describe motion and properties of object? • Simple Harmonic Motion/Oscillations (SHM/SHO) • Why? Spring • Rubber band – simple spring – Stretch it – pulls back – More you stretch it – the harder it pulls back – Some rubber bands harder to stretch than others • When compress a spring – still pushes back ! Sect 16.1 ! Sect 16.1 Springs - Hooke’s Law • Robert Hooke (1635-1703) Fapplied = kx • x = position relative to equilibrium has sign (direction) • k is spring constant (units = N/m) Cutnell & Johnson, Physics, 6th ed, Fig. 10.1 Applied Force & Spring Restoring Force • Force Applied by you is balanced by a Spring Restoring Force Fapplied = − Fspring Fspring = −kx Cutnell & Johnson, Physics, 6th ed, Fig. 10.5 Fspring FApplied Spring Constant of a Chromosome What is the spring constant of this newt chromosome? Fapplied = kx Force • 10 µm Poirier & Marko, J. Muscle Res. Cell Mot., 23:409, 2002 Extension (µm) F=kx 1 nN = k 1µm k = 1x10-9 N / 1x10-6 m k = 1x10-3 N/m Spring Constants from Graphs: Which of the curves represents the stiffest spring? Force 3 2 1) 1 2) 2 3) 3 4) All the same 1 Displacement Fapplied = kx Stiffest spring, largest force for fixed displacement Stiffest spring, largest spring constant Spring constant is equal to slope of Force vs Displacement Suppose you attach a mass to three identical springs. Compared to a mass attached to just one spring, it will: (assume pull 1cm in each case) 1) Require a larger force to stretch three springs than one. 2) Require the same force to stretch three springs as it takes to stretch one. 3) Require less force to stretch three springs than one. k1 k1 k1 k1 Free Body Diagram for block FSPRING FAPPLIED FSPRINGS FAPPLIED Effective spring constant 3k. The 3 springs in parallel act as 1 single spring 3 times as stiff. Hanging Masses • Can apply a known force by hanging a mass from a spring. • FAPPLIED = mg • Can find spring constant FAPPLIED = kx x kx mg A mass of 0.20 kg hangs from a spring, stretching it 0.10 m from it's equilibrium position. What is the spring constant of the spring? 1. 0.051 N/m 2. 0.50 N/m 3. 2.0 N/m 4. 19.6 N/m Fapplied = kx mg = kx (0.2kg)(9.8 m/s2) = k (0.10m) http://loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_mass_spring_novec.html Each of the spring is shown in its unstretched position, then stretched by hanging an object from it. Rank the spring constants. The grid allows a length reference. 1. kA > kB > kC > kD 2. kA = kB > kC = kD 3. kC = kD > kA = kB 4. kA = kD > kB = kC 5. kA > kB = kD > kC 6. kB = kC > kA = kD Look at how far it stretches from equilibrium. A is stiffer than B (kA>kB) since it stretches less than B with the same mass. A and D have the same spring constant. Twice as much force (double mass) stretches D twice as far as A. Thera-bands ™ Bands 30.5 cm long and 15.2 cm wide but come in different thicknesses – Yellow: 0.045” = 1.14 mm; k = 71 N/m for Δx < 10 cm –Red: 0.057” = 1.45 mm; k = 95 N/m for Δx < 15 cm –Green: 0.069” = 1.75 mm; k = 120 N/m for Δx < 15 cm – Blue: 0.085” = 2.16 mm; k = 140 N/m for Δx < 20 cm For small stretching (Δx less than about 10 to 20 cm), the F vs Δx lines are straight. For larger deflections, the lines are again straight, but the spring constant for each band is smaller than it was for small stretching. 60 Fapplied (N) 45 Yellow Red Green Blue 30 15 http://www.thera-band.com/ store/products.php? 0.00 0.18 0.35 0.53 0.70 ProductID=44 Dx (m) M. Hollis & P. Fletcher-Cook, Practical Exercise Therapy 4th ed. p. 111 0 Frequency and Period A mass is oscillating up and down on a spring. It completes 10 complete oscillations in 15 seconds. What is the frequency of oscillation? (1) 0.67 Hz (2) 1.5 Hz (3) 10 Hz (4) 15 Hz time T= # cycles 1 f= T f = 10 cycles/15 s = 0.67 Hz # cycles f = time SHM Position as function of time – sinusoidal function motion ↔ graph Note: Amplitude is the greatest displacement of the object from equilibrium Frequency – Physical Properties ! Sect 16.3 • How does the frequency of oscillation depend on physical properties of system? • Experiment – change masses and springs • Math Note: ω , T, f are Independent of Amplitude! Remember: f = 1/T, ω = 2π/T = 2πf If you know one, you know the other. Which is getting bigger and which is getting smaller can be confusing. A mass is hung from a spring and set into oscillation. It oscillates with a given frequency f1. Now a second identical spring is also attached to the mass (same k, same length). How does the new frequency compare to the old? 1)The new frequency is double the old 2)The new frequency is sqrt(2) times the old 3)The new frequency is the same as the old 4)The new frequency is 1/sqrt(2) times the old 5)The new frequency is half the old Double force with two springs. As if single spring of double strength. (keff = 2k) Stiffer spring, greater frequency. 1 f1 = 2π k m 1 f2 = 2π 2k = m 1 2 2π ( ) k = 2 f1 m f, T, ω, A: • Make sure you are clear on definitions and relations between them • How would you measure or calculate each? • Reference text definitions • Units – text, slides Frequency f – number of cycles per second – (1/s) or Hz Period T – time for one complete cycle – (s) – T = 1/f Angular frequency – also angular speed – 2πf – (rad/s) Amplitude – maximum distance from equilibrium – (m) # cycles f = time time T= # cycles Mass-Spring System - Horizontal Simulation – Horizontal mass and spring http://loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_mass_spring_novec.html Mass and Spring – PRS 1 http://loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_mass_spring_prs_a1.html Mass and Spring – PRS 2 http://loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_mass_spring_prs_v1.html Full Simulation http://loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_mass_spring_1.html Will place links on LON-CAPA Mass and Spring System • Force greatest at extremes – where spring stretched or compressed the most (zero at equilibrium) • Note: Amplitude is the greatest displacement of the object from equilibrium, (ie. the “Extremes”) • F=ma or a = F/m, so where the force is biggest, the acceleration is biggest. • Object speeds up as it heads towards equilibrium (F and a in direction of travel) • As it goes through equilibrium, F and a change direction, so starts to slow down. • Max v at equilibrium, zero v at extremes. The graph represents displacement of a mass in a mass-spring system. At what point(s) is the magnitude of the force at a maximum? (1) A (6) A and I (2) C (7) A, E, and I (3) E (8) C and G (4) G (9) A,C,G, and I (5) I The magnitude of the force is greatest at the extremes. maximum acceleration at what point(s)? A, E, and I minimum force & acceleration at what point(s)? C and G minimum (zero) velocity at what point(s)? A, E, and I maximum velocity at what point(s)? C and G Describe Temporal (Time) Behavior Compare to Circular motion • Frequency (1/s) or Hz • Period (s) = T = 1/f • x(t),v(t), a(t) θ = ωt x = A cos(ωt ) Comparison of Circular Motion and Harmonic Motion http:// loncapa.phy.ohiou.edu/res/ohiou/physlets/shm/shm_circle_1.html Position as a function of time x = A cos(ωt ) A = Amplitude ω = 2πf USE RADIANS! ω is angular speed or angular frequency Velocity as function of time v = −ωA sin(ωt ) Acceleration as function of time 2 a = −ω A cos(ωt ) Spring-Mass – Review formulas k m ω spring = f spring 1 = 2π m k T spring = 2π k m Note: T, f, ω are Independent of Amplitude! ω (lowercase greek omega) is angular frequency or angular speed xmax = A x = A cos (ω t ) v = − Aω sin (ω t ) 2 a = − Aω cos (ωt ) sin and cos range (-1 to 1) vmax = Aω amax = Aω 2 Suggest making list of equations while reading for reference in class