Download View

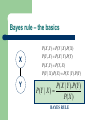
Cognitive Computer Vision
Kingsley Sage
[email protected]
and
Hilary Buxton
[email protected]
Prepared under ECVision Specific Action 8-3
http://www.ecvision.org
Lecture 5



Reminder of probability theory
Bayes rule
Bayesian networks
So why is Bayes rule relevant to
Cognitive CV?



Provides a well-founded methodology for
reasoning with uncertainty
These methods are the basis for our model of
perception guided by expectation
We can develop well-founded methods of
learning rather than just being stuck with handcoded models
Bayes rule: dealing with uncertainty

Sources of uncertainty e.g.:
–
–
–
–


Rev. THOMAS BAYES
1702-1761
ignorance
complexity
physical randomness
vagueness
Use probability theory to reason
about uncertainty
Be careful to understand what you
mean by probability and use it
consistently
–
–
frequency analysis
belief
Probability theory - reminder


p(x): single continuous value in the range [0,1].
Think of either as “x is true in 0.7 of cases”
(frequentist) of “I believe x = true with
probability 0.7”
P(X): often (but not always) used to denote a
distribution over a set of values, e.g. if X is
discrete {x=true, x=false} then P(X)
encompasses knowledge of both values.
p(x=true) is then a single value.
Probability theory - reminder

Joint probability
P( X , Y ) also written as P( X  Y )
P( X , Y )  P( X | Y ). p(Y )

Conditional probability
p( X | Y ) i.e. " X given Y"
Probability theory - reminder

Conditional independence

iff X  Y then P( X | Y )  p ( X )
P( X , Y )  P( X ).P(Y )
Marginalising
P( X , Y )  P( X | Y ).P(Y )
P( X )   P( X | Y ).P(Y )
Y
Bayes rule – the basics
X
P ( X , Y )  P (Y | X ).P( X )
P (Y , X )  P ( X | Y ).P(Y )
P ( X , Y )  P (Y , X )
P (Y | X ).P ( X )  P ( X | Y ).P (Y )
Y
P( X | Y ).P(Y )
P(Y | X ) 
P( X )
BAYES RULE
Bayes rule – the basics

As an illustration, let’s look at the
conditional probability of a hypothesis H
based on some evidence E
P( E | H ).P( H )
P( H | E ) 
P( E )
likelihood  prior
posterior 
probabilit y of evidence
Bayes rule – example
P( E | H ).P( H )
P( H | E ) 
P( E )







Consider a vision system used to
detect zebra in static images
It has a “stripey area” operator to help
it do this (the evidence E)
Let p(h=zebra present) = 0.02 (prior
established during training)
Assume the “stripey area” operator is
discrete valued (true/false)
Let p(e=true|h=true)=0.8 (it’s a fairly
good detector)
Let p(e=true|h=false)=0.1 (there are
non-zebra items with stripes in the
data set – like the gate)
Given e, we can establish
p(h=true|e=true) …
Bayes rule – example
p(e  true | h  true). p(h  true)
p(h  true | e) 
p( E )
p(e | h). p(h)
p ( h | e) 
p(e | h). p(h)  p(e | h). p(h)
0.8 * 0.02
p ( h | e) 
0.8 * 0.02  0.1* 0.98
0.016
p ( h | e) 
0.016  0.098
p(h | e)  0.1404
Note that this is an increase over the prior = 0.02
due to the evidence e
Interpretation




Despite our intuition, our detector does not seem very
“good”
Remember, only 1 in 50 images had a zebra
That means that 49 out of 50 do not contain a zebra
and the detector is not 100% reliable. Some of these
images will be incorrectly determined as having a zebra
Failing to account for “negative” evidence properly is a
typical failing of human intuitive reasoning
Moving on …




Human intuition is not very Bayesian (e.g.
Kahneman et al., 1982).
Be sure to apply Bayes theory correctly
Bayesian networks help us to organise our
thinking clearly
Causality and Bayesian networks are related
Bayesian networks


A
B

C

D
E


Compact representation of the joint
probability over a set of variables
Each variable is represented as a
node. Each variable can be discrete or
continuous
Conditional independence
assumptions are encoded using a set
of arcs
Set of nodes and arcs is referred to as
a graph
No arcs imply nodes are conditionally
independent of each other
Different types of graph exist. The one
shown is a Directed Acyclic Graph
(DAG)
Bayesian networks - terminology

A


B
C

D

E

A is called a root node and has a
prior only
B,D, and E are called leaf nodes
A “causes” B and “causes” C. So
value of A determines value of B
and C
A is the parent nodes of B and C
B and C are child nodes of A
To determine E, you need only to
know C. E is conditionally
independent of A given C
Encoding conditional independence
A
B
C
P( A, B, C )  P(C | A.B).P( A, B)
P( A, B)  P( B | A).P( A)
But C  A given B (conditional independence)
P(C | A, B)  P(C , B)
P( A, B, C )  P(C | B).P( B | A).P( A)
iN
P( X1, X 2 ,..., X N ) 

i 1
P( X i | parents( X i )
FACTORED
REPRESENTATION
Specifying the Conditional
Probability Terms (1)

{red,green,blue} {true,false}
B
A
For a discrete node C with discrete
parents A and B, the conditional
probability term P(C|A,B) can be
represented as a value table
a=
C
{true,false}
b=
p(c=T|A,B)
red
T
0.2
red
F
0.1
green
T
0.6
green
F
0.3
blue
T
0.99
blue
F
0.05
Specifying the Conditional
Probability Terms (2)
A
B
C
For a continuous node C with continuous
parents A and B, the conditional
probability term P(C|A,B) can be
represented as a function
p(c|A,B)

A
B
Specifying the Conditional
Probability Terms (3)
{true,false}
A
B
C
For a continuous node C with 1 continuous
parent A and and 1 discrete parent B, the
conditional probability term P(C|A,B) can be
represented as a set of functions (the
continuous function is selected according to a
“context” determined by B
p(c|A,B)

A
Directed Acyclic Graph (DAG)

A
B

C


D
E
Arcs encode “causal” relationships
between nodes
No more than 1 path (regardless of
arc direction) between any node
and any other node
If we added dotted red arc, we
would have a loopy graph
Loopy graphs can be approximated
by acyclic ones for inference, but
this is outside the scope of this
course
Inference and Learning

Inference
–
–

Calculating a probability over a set of nodes
given the values of other nodes
Two most useful modes of inference are
PREDICTIVE (from root to leaf) and
DIAGNOSTIC (from leaf to root)
Exact and approximate methods
–
–
Exact methods exist for Directed Acyclic Graphs
(DAGs)
Approximations exists for other graph types
Summary

Bayes rule allows us to deal with uncertain data
likelihood  prior
posterior 
probabilit y of evidence

Bayesian networks encode conditional independence.
Simple DAGs can be used n causal and diagnostic
modes
Next time …


Examples of inference using Bayesian
Networks
A lot of excellent reference material on
Bayesian reasoning can be found at:
http://www.csse.monash.edu.au/bai