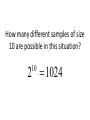Download AP Statistics: Section 9.1 Sampling Distributions

AP Statistics: Section 7.1
Sampling Distributions
What is the usual way to gain
information about some
characteristic of a population?
By taking a sample.
We must note, however, that the
sample information we gather may
differ from the true population
characteristic we are trying to
measure. Furthermore, the sample
information may differ from sample to
sample.
This sample-to-sample variability,
called
____________________________
sampling variabilty
poses a problem when we try to
generalize our findings to the
population. We need to gain an
understanding of this variability.
A parameter is
a number that describes a population.
A statistic is
a number computed from sample data.
In statistical practice, the value of a
parameter is unknown since we
cannot examine the entire
population. In practice, we often
use a statistic to estimate an
unknown parameter.
The population mean is
represented by the symbol ___

(Greek: Mu), the population
standard deviation by ___(Greek:

Sigma) and the population
p
proportion by ___.
The sample mean is represented by
the symbol ____
x (x bar), the sample
standard deviation by ____
s and the
sample population by ____
p̂ (p hat).
Example: Identify the number that
appears in boldface type as a
parameter or a statistic, and then
write an equation using the proper
symbol from above and the
number from the statement
A department store reports that
84% of all customers who use the
store’s credit plan pay their bills on
time.
paramter
p  .84
A consumer group, after testing
100 batteries of a certain brand,
reported an average of 63 hr of
use.
statistic
x  63 hours
We can view a sample statistic as a
random variable, because we have no
way of predicting exactly what statistic
value we will get from a sample, BUT,
given a population parameter, we
know how these sample statistics will
behave in repeated sampling.
Before we continue, we need to
discuss two important definitions:
The population distribution of a
variable is the distribution of
values of the variable among all
individuals in the population.
The sampling distribution of a
statistic is the distribution of
values taken by the statistic in all
possible samples of the same size
from the population.
Careful: The population
distribution describes the
individuals that make up the
population. A sampling distribution
describes how a statistic varies in
many samples of size n from the
population.
Consider flipping a coin 10 times.
We would expect to get 5 heads
out of the 10, but we realize that
we could also get 4 or 6 or 7 or
even 10. Let’s simulate this using
our graphing calculators.
MATH/PRB/7 :
.535
.135
WINDOW
Xmin  0
Xmax  1
Xscl  .1
Ymin  0
Ymax  10
Yscl  1
.6
How many different samples of size
10 are possible in this situation?
2  1024
10
Let’s increase our sample size to 25.
randBin(25 ,.5,20)/25  L1
.52
.120
.54
Hopefully, most of us found that as we
increased the sample size from 10 to 25,
the mean and the median of our sample
proportions became closer together and
both became closer to .5. Also we should
find that the standard deviation grows
smaller and our distribution of the sample
proportions became closer to being a
normal distribution.
Since a sampling distribution is a
distribution, we can use the tools
of data analysis to describe the
distribution: ________,
center
shape ________,
__________
outliers
spread and __________.
Remember to CUSS
Example: According to 2005
Nielsen ratings, Survivor:
Guatemala was one of the mostwatched TV shows in the US during
every week that it aired. Suppose
that the true proportion of US
adults who watched Survivor:
Guatemala was p = 0.37.
Describe the distribution of sample proportions
at the right for samples of size n = 100 of people
who watched Survivor: Guatemala.
center is approx. .37
no outliers
approx. Normal
range is .3
Describe the distribution of sample proportions
for samples of size n = 1000 of people who
watched Survivor: Guatemala.
center is approx. .37
no outliers
approx. Normal
range is .12
A statistic used to estimate a
parameter is unbiased if the mean of
its sampling distribution equals the
true value of the population
parameter.
The statistic is called an unbiased
estimator of the parameter.
An unbiased statistic will
sometimes fall above the true
value of the parameter and
sometimes below. There is no
tendency to overestimate or
underestimate the parameter,
hence the “unbiased.”
We will see in sections 7.2 & 7.3
that
are both unbiased
estimators of population
parameters.
The variability of a statistic is
described by the spread of its
sampling distribution.
This spread is determined by the
sampling design and the sample
size.
smaller
Larger samples give a ________
spread.
Assuming the population is larger
than the sample by at least a
factor of 10 and the sample sizes
are the same, the spread of the
sampling distribution is
approximately the same for any
population size.
This means that a statistic from an
SRS of size 2500 from the more
than 300 million residents of the
US is just as precise as an SRS of
size 2500 from the 750,000
inhabitants of San Francisco.
For a better understanding of bias and variability, think
of the center of a target as the true population
parameter and an arrow shot at the target as a sample
statistic.
high bias
low variability
low bias
high variability
high bias
high variability
low bias
low variability
Properly chosen statistics computed from random samples
of sufficient size will have low bias and low variability.