* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ch. 7.3
History of geometry wikipedia , lookup
Noether's theorem wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
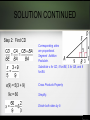
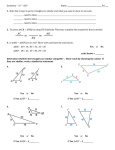
WARM UP 1. If ΔQRS ΔXYZ, identify the pairs of congruent angles and write 3 proportions using pairs of corresponding sides. R S Q Q ≅ X R ≅Y S ≅ Z Y QR RS SQ , , XY YZ ZX X Z TRIANGLE SIMILARITY: AA, SSS, & SAS OBJECTIVES • Prove certain triangles are similar by using AA, SSS and SAS. • Use triangle similarity to solve problems. ANGLE-ANGLE SIMILARITY • There are several ways to prove certain triangles are similar. • The following postulate, as well as the SSS and SAS Similarity Theorems, will be used in proofs just as SSS, SAS, ASA, HL, and AAS are used to prove triangles congruent. EXAMPLE 1 •Explain why the triangles are similar and write a similarity statement. By the Triangle Sum Theorem, m F = 47°, so C ≅ F. B ≅ E by the Right Angle Congruence Theorem. Therefore, ∆ABC ~ ∆DEF by AA ~. SIDE-SIDE-SIDE SIMILARITY SIDE-ANGLE-SIDE SIMILARITY EXAMPLE 2 Verify that the triangles are similar. ∆PQR and ∆STU Therefore ∆PQR ~ ∆STU by SSS ~. WARM UP Verify that ∆TXU . TXU ≅ ∆VXW VXW by the Vertical Angles Theorem. Therefore ∆TXU ~ ∆VXW by SAS ~. EXAMPLE 3 Explain why ∆ABE ~ ∆ACD, and then find CD . Step 1: Prove triangles are similar. A ≅ A by Reflexive Property of angles and since they are both right angles . Therefore ∆ABE ~ ∆ACD by AA ~. B≅ C SOLUTION CONTINUED Step 2: Find CD Corresponding sides are proportional. Segment Addition Postulate. Substitute x for CD, 5 for BE, 3 for CB, and 9 for BA. x(9) = 5(3 + 9) 9x = 60 Cross Products Property Simplify. Divide both sides by 9. TRY THIS… Explain why ∆RSV ~ ∆RTU, and then find RT. . Step 1: Prove triangle are similar. It is given that S ≅ T. R ≅ R by Reflexive Property of Congruency Therefore ∆ABE ~ ∆ACD by AA ~. SOLUTION CONTINUED Step 2: Find RT Corresponding sides are proportional. Segment Addition Postulate. Substitute RS for 10, 12 for TU, 8 for SV,. RT(8) = 10(12) 8RT = 120 RT = 15 Cross Products Property Simplify. Divide both sides by 9. CH. 7.3 HOMEWORK • Textbook pg. 473 "Think & Discuss" # 1 thru 4 • Textbook pg. 474 #2, 4, 6, & 12.