Download Intercellular Coupling Abnormalities in the Heart: Quantification from

UNIVERSITY OF CALGARY
Intercellular Coupling Abnormalities in the Heart:
Quantification from Surface Measurements and Impact on Arrhythmia Vulnerability
by
Amin Ghazanfari
A THESIS
SUBMITTED TO THE FACULTY OF GRADUATE STUDIES
IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE
DEGREE OF DOCTOR OF PHILOSOPHY
GRADUATE PROGRAM IN ELECTRICAL AND COMPUTER ENGINEERING
CALGARY, ALBERTA
MAY, 2016
c Amin Ghazanfari 2016
Abstract
Cardiac conduction velocity is one of the most important electrophysiological characteristics of the heart. Several cardiac dysfunctions and arrhythmia are caused by
slowed conduction velocity. Measurement of cardiac conduction velocity and other
physiological characteristics of the heart such as anisotropy ratio are challenged by
complex cardiac tissue structure and inaccurate measurement techniques. Diabetes
mellitus is an example of a condition that can alter conduction velocity by reducing
the electrical coupling between cardiac cells. Diabetes is also known to increase the
risk of arrhythmia by increasing the action potential duration of cardiac myocytes.
This thesis discusses a measurement method based on fitting ellipses to activation isochrones. Our results show that the intramural fiber rotation caused error in
conventional measurement methods used to estimate fiber orientation and anisotropy
ratio specially in thinner tissues. These errors are increased by optical mapping measurements specifically in thicker tissues.
We developed a mathematical model for the diabetic rabbit ventricular action potential and also used an existing model of the diabetic rat ventricular action potential.
We demonstrated the window of vulnerability to reentrant arrhythmia for healthy and
diabetic models of both rabbit and rat. Connexin lateralization was modelled in the
diabetic models by reducing the gap junction conductivity in the lateral direction.
Results demonstrated that window of vulnerability in diabetic rat is smaller than in
healthy rat. On the contrary, diabetic rabbit was more vulnerable to reentry than
healthy rabbit. The ATP-dependent potassium channel was added to the models and
the results demonstrated that diabetic models are more vulnerable to reentry when
ischemia occurs and IKATP channels open consequently.
ii
Acknowledgements
A PhD thesis is truly a marathon journey which would not be possible without the
support and guidance of many individuals. I would like to express my gratitude
towards all of them who helped transform my research work into a successful PhD
thesis.
There is possibly no transformation capable of mapping my deep appreciation for
my supervisor, Dr. Anders Nygren, into few lines of acknowledgements! He has provided me with invaluable continuous guidance and support, while offering full freedom
of exploring new ideas and research directions. His insights and troubleshooting skills
have strengthened this study significantly.
I would like to extend my thanks to Dr. Vigmond, for his concise and precise
inputs to my research. His software alongside with his insights and comments helped
me develop major parts of this study.
Over the years, I have also been fortunate to share a lab with some formidably
intelligent fellow students, who will all go on to make a difference, whether it is in
this field or another. In particular, thanks to Marcela Rodriguez for not only helping
me with experimental studies in this study, but also for being the best friend I have
had here.
Over the past years, my roommates and friends were always beside me. I thank
them for all kind of support they provided especially doing the dishes! Thank you
Ehsan, Hesam, Mohsen and Alireza.
iii
Dedication
To my Family who I deprived myself from their presence beside me:
Maman, your endless love for me helped me endure missing you.
Baba, your support always helped me keep going on.
Shiva, the smile you put on my face whenever I talked to you made my life beautiful.
Hadi and Ali, I know how much we are proud of each other as brothers and friends.
& to all other sacrifices I made.
Table of Contents
Abstract . . . . . . . . . . . . . . . . . . . . . .
Acknowledgements . . . . . . . . . . . . . . . .
Dedication . . . . . . . . . . . . . . . . . . . . .
Table of Contents . . . . . . . . . . . . . . . . . .
List of Tables . . . . . . . . . . . . . . . . . . . .
List of Figures . . . . . . . . . . . . . . . . . . . .
List of Symbols . . . . . . . . . . . . . . . . . . .
1
Motivation . . . . . . . . . . . . . . . . . . .
2
The Heart . . . . . . . . . . . . . . . . . . .
2.1 Anatomy of the Heart . . . . . . . . . . . .
2.1.1 Heart chambers and circulation . . .
2.1.2 Cardiac cells . . . . . . . . . . . . . .
2.1.3 Cardiac tissue . . . . . . . . . . . . .
2.1.4 Cardiac conduction system . . . . . .
2.2 Electrical Activity of the Heart . . . . . . .
2.2.1 The cardiac action potential . . . . .
2.2.2 Propagation in cardiac tissue . . . .
2.2.3 Excitation-Contraction coupling . . .
2.2.4 Electrocardiogram (ECG) . . . . . .
2.3 Arrhythmia and Fibrillation . . . . . . . . .
2.3.1 Types of arrhythmia . . . . . . . . .
2.3.2 Reentry . . . . . . . . . . . . . . . .
2.3.3 Gap junctions and arrhythmias . . .
2.4 Diabetes and the Heart . . . . . . . . . . . .
2.4.1 Types of Diabetes . . . . . . . . . . .
2.4.2 Diabetic Heart . . . . . . . . . . . .
2.4.3 Electrophysiological Complications of
2.4.3.1 ECG abnormalities . . . . .
2.4.3.2 Ion channel remodelling . .
2.4.3.3 Connexin lateralization . .
2.4.3.4 Calcium abnormalities . . .
3
Biophysical Mechanisms . . . . . . . . . . .
3.1 Cell Membrane . . . . . . . . . . . . . . . .
3.1.1 The Nernst-Planck Equation . . . . .
3.1.2 Nernst Equilibrium Potential . . . .
3.1.3 Electrical Model of Cell Membrane .
3.2 Ionic Current Models . . . . . . . . . . . . .
3.2.1 Hodgkin & Huxley Model . . . . . .
3.2.2 Markov Models . . . . . . . . . . . .
v
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
Diabetes
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ii
iii
iv
v
viii
ix
xi
1
4
4
4
6
8
10
12
12
15
16
17
19
19
21
24
25
26
26
28
28
28
28
31
33
33
33
34
35
36
37
39
3.3
3.4
4
4.1
4.2
4.3
4.4
4.5
4.6
5
5.1
5.2
Signal Propagation in Cardiac Tissue . . . . . . . . . . . . . . . . .
3.3.1 Bidomain Modelling . . . . . . . . . . . . . . . . . . . . . .
3.3.2 Monodomain modelling . . . . . . . . . . . . . . . . . . . . .
Numerical Methods . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Euler’s method . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.2 Finite Element Method . . . . . . . . . . . . . . . . . . . . .
Cardiac physiological characteristics measurements . . . . . . . . .
Chapter Specific Background . . . . . . . . . . . . . . . . . . . . . .
Cardiac Optical Mapping . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1 Voltage-sensitive dye . . . . . . . . . . . . . . . . . . . . . .
4.2.2 Imaging system . . . . . . . . . . . . . . . . . . . . . . . . .
Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.1 Computational Model . . . . . . . . . . . . . . . . . . . . .
4.3.2 Data Processing . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3 Estimation of Epicardial Fiber Orientation . . . . . . . . . .
4.3.4 Estimation of Anisotropy Ratio (AR) . . . . . . . . . . . . .
4.3.5 Optical Mapping Model . . . . . . . . . . . . . . . . . . . .
4.3.6 Experimental Methods . . . . . . . . . . . . . . . . . . . . .
Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.4.1 Simulation Results . . . . . . . . . . . . . . . . . . . . . . .
4.4.1.1 Observations based on isochrones . . . . . . . . . .
4.4.1.2 Conduction velocities . . . . . . . . . . . . . . . . .
4.4.1.3 Alternative estimates based on conduction velocities
4.4.1.4 Effect of optical mapping . . . . . . . . . . . . . .
4.4.1.5 Effect of photon scattering . . . . . . . . . . . . . .
4.4.1.6 Effect of spatial discretization . . . . . . . . . . . .
4.4.2 Experimental Results . . . . . . . . . . . . . . . . . . . . . .
Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.1 Effect of fiber rotation and wall thickness . . . . . . . . . . .
4.5.2 Effect of transmural conductivity . . . . . . . . . . . . . . .
4.5.3 Effect of optical mapping . . . . . . . . . . . . . . . . . . . .
4.5.4 Implication for experimental measurements . . . . . . . . . .
4.5.5 Study limitations . . . . . . . . . . . . . . . . . . . . . . . .
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diabetes and Vulnerability to Arrhythmias . . . . . . . . . . . . . .
Chapter Specific Background . . . . . . . . . . . . . . . . . . . . . .
Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.1 Rat Model . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.2 Rabbit Model . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.2.1 Summary of the rabbit mathematical model . . . .
5.2.2.2 Changes in diabetic rabbit . . . . . . . . . . . . . .
5.2.3 ATP-dependent potassium channels (IKATP ) . . . . . . . . .
vi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
42
42
45
46
46
48
54
54
56
57
57
57
57
59
60
62
62
63
65
65
65
68
69
70
72
75
77
80
80
81
82
82
85
86
88
88
91
91
91
91
93
93
5.2.4 Spontaneous Calcium Release . . . . . . . . . . . . . . . . . . 94
5.2.5 Connexin Lateralization . . . . . . . . . . . . . . . . . . . . . 94
5.2.6 Tissue Simulations . . . . . . . . . . . . . . . . . . . . . . . . 95
5.2.7 Reentrant Arrhythmias . . . . . . . . . . . . . . . . . . . . . . 95
5.2.8 Conduction Reserve . . . . . . . . . . . . . . . . . . . . . . . . 96
5.3 Results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
5.3.1 Single cell APD is increased by diabetes . . . . . . . . . . . . 97
5.3.2 IKATP shortens APD more in diabetic tissue than in healthy tissue 97
5.3.3 Connexin lateralization does not affect source-sink relationship
for an ectopic beat . . . . . . . . . . . . . . . . . . . . . . . . 100
5.3.4 Vulnerability to reentry . . . . . . . . . . . . . . . . . . . . . . 102
5.3.5 Rabbit and rat have the same conduction reserve . . . . . . . 103
5.3.6 Rabbit and rat have different APD restitution . . . . . . . . . 106
5.4 Discussion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
5.4.1 Diabetes decreases arrhythmia vulnerability in rat . . . . . . . 108
5.4.2 Diabetes increases arrhythmia vulnerability in rabbit . . . . . 109
5.4.3 Diabetes did not change the source-sink relationship . . . . . . 111
5.4.4 Diabetes has different effects on arrhythmia vulnerability in
different species . . . . . . . . . . . . . . . . . . . . . . . . . . 112
5.4.5 Study limitations . . . . . . . . . . . . . . . . . . . . . . . . . 114
6
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
6.1 Significant findings . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
6.1.1 Cardiac measurements . . . . . . . . . . . . . . . . . . . . . . 115
6.1.2 Diabetes and arrhythmia vulnerability . . . . . . . . . . . . . 116
6.2 Clinical relevance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
6.3 Modelling limitations and future work . . . . . . . . . . . . . . . . . 118
6.4 Future work . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
Bibliography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
A
Simulation Time . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
B
Copyright Permissions . . . . . . . . . . . . . . . . . . . . . . . . . . 141
vii
List of Tables
3.1
4.1
4.2
4.3
4.4
4.5
4.6
Extra- and intracellular concentrations and Nernst potential for a ventricular myocyte. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
Measured epicardial fiber direction and anisotropy . . . . . . . . .
Measured wave propagation parameters . . . . . . . . . . . . . . .
Angle of propagation for different spatial discretization . . . . . .
Anisotropy ratio for different spatial discretization . . . . . . . . .
Longitudinal conduction velocity for different spatial discretization
Transverse conduction velocity for different spatial discretization .
70
72
75
76
76
77
.
.
.
.
.
.
.
.
.
.
.
.
A.1 Simulation details: number of runs, simulation times, and total time
for each simulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
viii
List of Figures and Illustrations
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.13
Heart chambers, veins, and arteries . . . . . . . . . . . . . . . . . . .
Circulation system of the human body . . . . . . . . . . . . . . . . .
Cell membrane phospholipid bilayer with embedded proteins. . . . . .
Cardiac conduction system . . . . . . . . . . . . . . . . . . . . . . . .
Normal cardiac action potential and its phases . . . . . . . . . . . . .
Main ionic currents of the cardiac action potential . . . . . . . . . . .
Gap junction between two cells . . . . . . . . . . . . . . . . . . . . .
intracellular Ca2+ dynamics . . . . . . . . . . . . . . . . . . . . . . .
The schematic representation of a human ECG . . . . . . . . . . . .
Schematic representation of an anatomical reentry . . . . . . . . . . .
Simulation of functional reentry using S1-S2 stimulation . . . . . . .
Quantification of Cx43 in STZ-diabetic and healthy rat . . . . . . . .
The fraction of immunofluorescence labelled Cx43 associated with intercalated discs (ICD) and that associated with lateralized Cx43 for
both control and STZ-diabetic rat . . . . . . . . . . . . . . . . . . . .
2.14 Analysis of Cx43 lateralization . . . . . . . . . . . . . . . . . . . . . .
5
7
8
12
13
14
16
18
19
22
23
29
3.1
3.2
3.3
3.4
3.5
3.6
3.7
37
40
41
42
43
49
Electric circuit model of the cellular membrane . . . . . . . . . . . .
A simple two-state Markov model . . . . . . . . . . . . . . . . . . . .
Different configurations of an ion channel . . . . . . . . . . . . . . . .
Equivalent Markov model of Hodgkin-Huxley sodium current . . . . .
Equivalent bidomain circuit diagram of single cell. . . . . . . . . . . .
A solution region and its finite element discretization. . . . . . . . . .
A triangular element used in FEM calculations. Local nodes are numbered as 1, 2, and 3. . . . . . . . . . . . . . . . . . . . . . . . . . . .
Schematic diagram showing arrangement of the major components of
the imaging system . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Fitting an ellipse to an isochrone . . . . . . . . . . . . . . . . . . . .
4.3 Activation time isochrones on the epicardial surface . . . . . . . . . .
4.4 Angle of wave propagation versus time . . . . . . . . . . . . . . . . .
4.5 Angle of wave propagation versus tissue thickness . . . . . . . . . . .
4.6 Anisotropy ratio versus tissue thickness for different transmural conductivities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7 Transverse (θt ) and longitudinal (θl ) conduction velocity . . . . . . .
4.8 Different approaches to model emission light . . . . . . . . . . . . . .
4.9 Isochrones based on the simulations of optical mapping with and without the scattering effect . . . . . . . . . . . . . . . . . . . . . . . . .
4.10 Experimental results . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
31
50
4.1
ix
58
61
65
66
67
68
69
73
74
78
4.11 Experimentally obtained activation isochrones from a rat left ventricular free wall . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
Schematic diagram of the rabbit model from Mahajan et al . . . . . .
S1-S2 stimulation protocol . . . . . . . . . . . . . . . . . . . . . . . .
Changes in diabetic rat ionic currents . . . . . . . . . . . . . . . . . .
Changes in diabetic rabbit ionic currents . . . . . . . . . . . . . . . .
Effect of IKATP opening on the rat action potential . . . . . . . . . . .
Effect of IKATP opening on the rabbit action potential . . . . . . . . .
Spontaneous Ca2+ release propagation through the tissue. . . . . . .
Window of vulnerability for healthy and diabetic rat models . . . . .
Window of vulnerability for healthy and diabetic rabbit models . . .
Relationship between conduction velocity and conductivity for rat and
rabbit models. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.11 S1S2 APD restitution curves in single epicardial ventricular cells . . .
x
79
92
96
98
99
100
101
102
104
105
106
107
List of Symbols, Abbreviations and Nomenclature
Symbol
Definition
AP
Action Potential
APD
Action Potential Duration
AF
Atrial Fibrillation
AR
Anisotropy Ratio
ATP
Adenosin Tri-Phosphate
AV
Atrioventricular
CHD
Coronary Heart Disease
CHF
Congestive Heart Failure
CICR
Ca2+ -Induced Ca2+ Release
CV
Conduction Velocity
CVD
Cardiovascular Disease
Cx
Connexin
DAD
Delayed After Depolarization
DM
Diabetes Mellitus
DTMRI
Diffusion Tensor Magnetic Resonance Imaging
EAD
Early After Depolarization
ECC
Excitation-Contraction Coupling
ECG
Electrocardiogram
GJ
Gap Junction
JSR
Junctional Sarcoplasmic Reticulum
LA
Left Atrium
LV
Left Ventricle
xi
MI
Myocardial Infarction
Vm
Membrane Potential
NCX
Na+ /Ca2+ Exchanger
NSR
Network Sarcoplasmic Reticulum
OM
Optical Mapping
PVC
Premature Ventricular Complex
RA
Right Atrium
RV
Right Ventricle
RyR
Ryanodine Receptor
SA
Sinoatrial
SERCA
Sarco-Endoplasmic Reticulum Ca2+
SR
Sarcoplasmic Reticulum
STZ
Streptozotocin
VF
Ventricular Fibrillation
VT
Ventricular Tachycardia
xii
Chapter 1
Motivation
Cardiac conduction velocity, the speed with which an electrical impulse propagates
through the cardiac tissue, is one of the most important electrophysiological characteristics of the heart. The importance of conduction velocity arises in the context of
cardiac rhythm and arrhythmia. Slowed myocardial conduction velocity is associated
with an increased risk of re-entrant activities that can lead to cardiac arrhythmia.
Conduction velocity in the tissue depends on the cell excitability and the electrical
coupling between the cells. Excitability is controlled by sodium channel conductivity,
while coupling is related to the gap junction conductivity. These determinants are
altered by a wide range of pathophysiological conditions.
Gap junctions are non-selective membrane channels that form low resistance cellto-cell connections to ease intercellular current as well as the transfer of ions, amino
acids, and nucleotides. In general, cardiac cells express gap junctions at higher densities toward the ends of cells compared to their sides, resulting in higher conductivity in
the longitudinal direction. These channels are composed of proteins called connexins
(Cx). Changes in connexin distribution and functionality can alter gap junction function and thereby reduce intercellular coupling. Diabetes mellitus is known to cause
migration of the connexins from cell ends to cell sides, which is known as connexin
lateralization.
This thesis mainly focuses on the intercellular coupling and cardiac conduction
velocity. Chapter 2 is a medical and physiological background of the topics covered
in this thesis. The biophysical mechanism and modelling techniques are discussed in
1
detail in Chapter 3. The mathematical requirements and the numerical methods are
provided in this chapter.
Chapter 4 provides simulations to discuss different methods of measuring elctrophysiological characteristics of the heart such as anisotropy ratio, fiber orientation,
and conduction velocity. The effects of tissue thickness and intercellular coupling on
these parameters are also discussed in this chapter. Experimental data are provided
to support simulation results.
Diabetes mellitus is a chronic progressive disease that results in microvascular
and macrovascular complications. Other than the acute glucose level abnormalities,
diabetes also causes chronic renal failure, retinal damage, nerve damage, micro vascular damage, cardiovascular disease and poor healing which can lead to gangrene and
even amputation. Diabetes is a significant independent risk factor for heart failure and
there is a substantial number of patients with both diabetes and heart failure. The
most well documented electrophysiological dysfunction of diabetes is the QT interval
prolongation in the electrocardiogram, which is a direct effect of the prolongation of
the ventricle action potential. Conduction of electrical activation through the heart
is one of the less thoroughly studied effects of diabetes. Chapter 5 is concerned with
this aspect of cardiac electrophysiological effects and variations of diabetes. Different species have different cardiac action potential duration and morphology. These
differences can cause species-dependent characteristics, which can lead to distinct behaviors in pathophysiological situations. This chapter provides simulations related to
the electrophysiological differences in diabetic rat and rabbit models and how these
differences affect the vulnerability of each species to the re-entrant arrhythmia.
Finally, Chapter 6 provides concluding remarks on the results presented in this
work. Future complementary research that can be conducted from this work is also
2
introduced in this chapter.
3
Chapter 2
The Heart
The heart is a muscular pump responsible for circulating blood in the body. This vital
organ beats approximately 100,000 times each day, pumping roughly 8,000 liters of
blood per day [1]. It functions effectively thanks to a synchronized relation between
its electrical, mechanical and fluidic systems. This chapter provides an overview of the
anatomy of the heart, contraction, and its normal and disorderly electrical activities.
2.1 Anatomy of the Heart
2.1.1 Heart chambers and circulation
The heart is located between the lungs in the middle of the chest, behind and slightly
to the left of the sternum. A double-layered membrane called the pericardium surrounds the heart like a sac. The inner layer of the pericardium is attached to the heart
muscle, while the outer layer covers the heart’s major blood vessels and is attached
to the spinal column and diaphragm. A lubricant fluid separates the two layers of
membrane, letting the heart move as it beats.
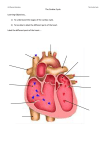
As shown in Fig.2.1, the human heart is made up of four muscular chambers, the
left and right atria (upper chambers) alongside with the left and right ventricles (lower
chambers—LV and RV respectively). The left and right chambers are separated by
a muscular wall called the septum. The left ventricle is the largest and strongest
chamber in the heart as it pumps the blood through the whole body.
The blood is received at the right atrium by the superior and inferior vena cava
4
Superior
vena cava
Aorta
Left
Atrium
Right
Atrium
Tricuspid
valve
Inferior
vena cava
Mitral
valve
Aortic
valve
Left
Ventricle
Right
Ventricle
Pulmonary
valve
Figure 2.1: Heart atria and ventricles, valves (shown by arrows), main arteries and veins.
Blood is received from inferior and superior vena cava and pumped to lungs (pulmonary
circulation shown in blue) and then returned to the heart and pumped to the whole body (main
circulation shown in red); Adapted under a Creative Commons Attribution 2.5 Unported
license from original work by Dcoetzee; Online: https://goo.gl/haEdO8; License: http:
//goo.gl/TGFja
veins. Blood travels from the right atrium to the right ventricle through the right atrioventricular valve known as the tricuspid valve. When the right ventricle contracts,
the tricuspid valve closes to prevent the backflow of the blood to the right atrium.
Blood traveling out of the right ventricle passes through the pulmonary valve to enter
the pulmonary trunk. The blood then flows into left and right pulmonary arteries
and into the lungs. The vessels branch into many thin walled vessels called capillaries
where the gas exchange occurs (pulmonary circulation).
Oxygenated blood is returned to the left atrium by the pulmonary veins. When
the left atrium contracts, the blood flows into the left ventricle through the bicuspid
valve, also known as the mitral valve. The mitral valve allows the blood to flow from
5
the left atrium to the left ventricle and prevents blood flow in opposite direction.
The strong and thick walls of the left ventricle (approximately 3 times thicker than
the right ventricle) provide a contraction with sufficient pressure to pump the blood
through the whole body. Contraction of the left ventricle closes the mitral valve and
pumps the blood out of the left ventricle to the aorta through aortic valve. The aorta
connects to the arterial system and delivers oxygenated blood to the rest of the body
(systemic circulation). Figure 2.2 shows pulmonary and systemic circulations in the
human body.
The heart itself receives the blood from the coronary arteries which are the first
vessels that branch off the aorta. Like other arteries, they divide into a fine capillary
network to perfuse the heart muscle with the oxygen-rich blood. This blood returns
to the heart by the coronary sinus which drains into the lower part of the right atrium.
2.1.2 Cardiac cells
The heart is constructed from electrically excitable cells like all muscle tissues. The
cardiac muscle cells are called cardiomyocytes or briefly myocytes, and are surrounded
by a cell membrane. The cell membrane of a myoycte, also known as sarcolemma, is
mainly comprised of phospholipids, cholesterol, glycolipids, and membrane proteins.
The cell membrane separates the intracellular fluid from extracellular space with a
phospholipid bilayer. Phospholipids are molecules made up of a hydrophilic head
and hydrophobic tail. As a result they form a bilayer as shown in Fig. 2.3. The
resulting bilayer prevents molecules such as water and ions from traveling between
intra and extracellullar fluids. However, there are specialized embedded proteins in
the membrane that allow some small molecules and ions to pass the membrane. These
proteins that are known as “ion channels”, function as highly selective pores that
6
Figure 2.2: Circulation system of the human body; the cardiovascular system has two
distinct circulatory paths, pulmonary circulation and systemic circulation. Blood movement
from the heart to the lungs which is done by right chambers is called pulmonary circulation.
Systemic circulation is the movement of the blood to the rest of the body. Adapted under
a Creative Commons Attribution 3.0 Unported license from original work by OpenStax
College; Online: https://goo.gl/IWbnUF; License: https://goo.gl/haEdO8
7
Phospholipid
Bilayer
Membrane
Proteins
Figure 2.3: Cell membrane phospholipid bilayer with embedded proteins.
can transport ions between cell interior and extracellular fluid without consuming
or providing energy solely relying on electrical and chemical gradients of the ions.
Ion channels open and close in different voltage, time, and chemically gated forms to
allow specific ions to cross the cell membrane.
Ion channels are not the only proteins embedded in the sarcolemma. Other types
of proteins such as pumps, ion exchangers, and co-transporters consume energy to
move ions in their own selective and regulatory manner. In contrast with ion channels,
ion pumps consume energy from adenosine triphosphate (ATP) to move ions across
the cell membrane against their electrical or chemical gradients. These proteins are
essential in order to maintain the concentration gradients of K+ , Na+ , and Ca2+
across the cell membrane. This gradient across the membrane results in a resting
electric potential across the membrane. The electrical model of cell membrane and
ionic currents will be discussed in detail in Section 3.1.
2.1.3 Cardiac tissue
The heart pumps the blood continuously and strongly during the whole life without
any rest, so cardiac muscle must have incredibly high contractility and endurance.
8
Cardiac muscle cells are striated and branched. Each cardiac myocyte is attached at
its end to adjoining myocytes by a membrane called intercalated disc (ICD). These
myocytes form long fiber bundles and in the atrial fibers they are arranged in concentric circles and wrapped around the atria.
Over the past centuries, numerous efforts have been made to improve the understanding of the fiber structure of the heart. These efforts progressed with the
development of more sophisticated analysis techniques. The term “fiber” has been
used differently at different size scales. Throughout this work, “fiber” refers to the
general axial direction of the myocytes in a specific cardiac site. Therefore, by this
definition, fiber orientation is analogous to the direction of “grain” in wood.
Initially, “blunt-dissection” techniques were applied by teasing apart the myocardium with fingers and “blunt” tools such as scissors. These techniques enable
only basic qualitative description of myocardial fiber architecture. Lower reported
that fiber orientation is not homogeneous in the wall in 1660 [2]. In 1849, Ludwig
described the strands of myocytes in the wall as a figure-of-eighth as they proceed
from base of right ventricle (RV) to the apex of RV, and then back to the base of left
ventricle (LV) [3].
Modern histological analysis was employed in ultra-thin sliced tissue sections (less
than 10µm thickness) to quantitatively measure two dimensional myocardial fiber
architecture. In 1969, Streeter and colleagues performed the first quantitative measurement of fiber orientation in the LV wall of dog hearts [4]. They stated that the
fiber angle transitioned smoothly from 60◦ at endocardial to -60◦ at epicardial surface. By their definition, fiber angle is the angle between fiber orientation and local
circumferential axis.
Caulfield and Brog used scanning electron microscopy and demonstrated that in9
dividual myocytes are grouped with other myocytes and surrounded by an extensive
extracellular collagen network [5]. Quantitative characterization of the grouped myocyte structure showed that myocytes are integrated into laminar layers that typically
are 4 cells thick and predominantly lie in the planes spanned by myofiber orientation
and radial direction [6].
Diffusion tensor magnetic resonance imaging (DTMRI) has been proposed recently
as an alternative method for non-invasive 3D characterization of myocardial fiber and
sheet structure. The tree-dimensional fiber structure of the heart has been successfully
reconstructed at high resolution using DTMRI [7].
The anisotropic (directionally-dependent) architecture of cardiac tissue is critical
in coordinating electrical propagation and providing efficient force production in the
heart. Anisotropy observed at the organ and tissue level, with the alignment of the
cardiomyocytes into fibers and sheets, can also be traced down to the cellular level. Individual cardiomyocytes naturally exhibit an elongated morphology that contributes
to the electrical and mechanical anisotropy. Electrical anisotropy at the cellular level
is also attributed to the distribution of gap junctions. In cardiac myocytes, gap
junctions are preferentially located at cell ends on the ICD.
2.1.4 Cardiac conduction system
Cardiac myocytes are constantly responsible for contraction and relaxation. They are
able to contract in response to an electric impulse. This property is known as cardiac
“excitability”. In addition, some regions of the cardiac tissue are responsible for
initiating and orchestrating the electrical impulses causing the mechanical contraction
of the cardiac muscle. Unlike the rest of the tissue, these regions undergo spontaneous
excitation at systematic frequent intervals, establishing a timely delivery of stimuli
10
to the rest of the heart. This property is called “automaticity”.
Figure 2.4 shows a diagram of the cardiac conduction system. The sinoatrial (SA)
node is embedded in the posterior wall of the right atrium near the superior vena cava.
For normal contraction, excitation originates from the SA node. This region contains
pacemaker cells capable of initiating the heart beats and is therefore known also as
the cardiac pacemaker. The impulse generated by the SA node spreads through the
atria and initiates their contraction. The action potential spreads through cell to
cell contacts and reaches the atrioventricular (AV) node. The atria and ventricles are
electrically insulated and the AV node is the only electrical connection between them.
The conduction through the AV node is slow and as a result it causes a successive
conduction delay from end to end for stimuli. This property inhibits uncontrolled cellto-cell activation of ventricles unlike the atria. This delay is also important to ensure
the atrial contraction is complete before the ventricles begin to contract. Otherwise
the powerful contraction of the ventricles would close the AV valves preventing the
blood flow from the atria to the ventricles.
As shown in Fig. 2.4, the ventricular conduction system consists of the bundle of
His, that branches into the left and right bundle branches, and the Purkinje fibers.
Once an impulse passes the AV node, it enters the bundle of His and travels to the
interventricular septum to enter the left and right bundle branches. Both the branches
descend along the left and right septal surfaces toward the apex of the heart, turn, and
spread over the whole endocardial surface. As the branches bifurcate, the Purkinje
fibers connect to the myocytes and conduct the action potential very rapidly. They
are responsible for the synchronized depolarization of the ventricles. The Purkinje
fibers radiate from the apex toward the base of the heart and therefor ventricular
contraction begins at the apex toward the base to completely pump the blood and
11
Figure 2.4: Schematic of the cardiac conduction system; Impulse originates from the
sinoatrial (SA) node, propagates through the atria to reach the atrioventricular (AV) node.
After a delay the impulse passes through His bundle, branches into the left and right bundle
branches to reach the Purkinje fibers causing a synchronized excitation of the ventricles.
Adapted and modified under a Creative Commons Attribution 3.0 Unported license from
original work by Madhero88; Online: https://goo.gl/GiAMbk; License: https://goo.gl/
haEdO8
empty the ventricles into the aorta and pulmonary trunk.
2.2 Electrical Activity of the Heart
2.2.1 The cardiac action potential
Action potentials are generated by the movement of ions through the transmembrane
ion channels in the cardiac cells. The cardiac myocyte has a negative membrane
potential when at rest, which is caused by the difference in ionic concentrations and
conductances across the membrane of the cell during the resting phase of the action
potential. The normal resting membrane potential in the ventricular myocardium is
12
40
1
2
membrane potential (mV)
20
0
-20
0
-40
3
-60
-100
4
4
-80
0
50
100
150
200
250
300
350
time (ms)
Figure 2.5: Normal cardiac action potential and its phases; Phase 0: depolarization, phase
1: early repolarization, phase 2: plateau, phase 3: repolarization, and phase 4: resting
potential. Action potential is generated from simulation of a rabbit ventricular myocyte
model [96].
about -75 to -85 mV.
The different phases of an action potential are shown in Fig. 2.5. When the cell
is stimulated and the membrane potential passes a threshold (approx. 20mV above
the resting potential), it goes through the depolarization phase which is due to the
opening of Na+ channels. A massive influx of Na+ raises the membrane potential and
consequently causes the inactivation of sodium channels, resulting in a very shortlived inward current (phase 0). In the SA node and the AV node, phase 0 of an action
potential is due to the inward Ca2+ current through the L-type Ca2+ channels (ICaL ).
After the upstroke, there is an abrupt drop in the membrane potential (phase 1)
due to the opening of the transient outward K+ channels (Ito ). The most important
difference between cardiac action potentials and neural action potentials is the plateau
13
8
5
IKr
-5
-10
-15
INa
-20
-25
IKs
6
current (nA/nF)
current (nA/nF)
0
Ito
4
IK1
2
0
ICaL
0
50
100
150
200
250
300
-2
350
time (ms)
0
50
100
(a)
150
200
time (ms)
250
300
350
(b)
Figure 2.6: Main ionic currents of the cardiac action potential; major underlying inward
(a) and outward (b) currents are generated from simulation of a rabbit ventricular myocyte
model [96]. In (a) INa is clipped: min INa ≈ −160µA/cm2 . Stimulus applied at t = 50ms
phase (phase 2). This plateau is due to the inward Ca2+ current (ICaL ) which is in a
relative balance with outward K+ current. With inactivation of Ito , rapid and slow
delayed rectifier K+ currents (IKs and IKr ) activate and gradually the membrane
repolarization starts. With the closure of the L-type Ca2+ channels and opening of
inward rectifier K+ current (IK1 ), the action potential goes to the rapid repolarization
phase. IK1 also plays an important role in setting the resting potential (phase 4). The
major inward and outward currents are shown in Fig. 2.6.
The cardiac refractory period is when a cell has not completely recovered from
the previous action potential and is not excitable so it does not respond to a new
stimulus. The cardiac refractory period is divided into an absolute refractory period
and a relative refractory period. In the absolute refractory period, a cardiac myocyte
cannot fire a new action potential. During the relative refractory period, a new
action potential can be elicited in certain circumstances (such as a large stimulus
magnitude).
14
2.2.2 Propagation in cardiac tissue
When a region of the cardiac tissue undergoes an action potential, the current flows
into the neighboring cells through intercellular gap junctions. An action potential is
generated from the depolarizing current flow of a neighboring cell. Then, the action
potential propagates from an excited cell to the neighboring resting cells. This process
is facilitated by low-resistance protein pathways called gap junctions.
Gap junctions (GJs) regulate the amount of current that flows to the neighboring cells (sink) from depolarized cells (source). They form transmembrane channels
that connect the cytoplasmic compartments of neighboring cells to facilitate highconductivity, non-selective conduction. This results in an orderly propagation of
electrical stimulus, and hence, synchronized contraction of the heart.
Each gap junction consists of two connexon hemi-channels, one embedded in each
membrane of the neighboring cells. Each connexon consists of six protein subunits
called connexins (Cx). Figure 2.7 shows the schematic representation of gap junctions and connexins. Almost 20 different types of connexins have been identified in
mammalian cells [8], of which Cx40, Cx43, and Cx45 are the main isoforms in the
myocardium. It is common to identify tissue region from the Cx type of the cell; i.e.
the Cx40 can be found in atria, Cx43 is mainly abundant in ventricles, and Cx45 is
exclusively found in the cardiac conduction system [9].
Gap junctions play an important role in the maintenance of normal conduction
velocity (CV) of the action potential. As the GJ conductivity decreases (cells become
less coupled), the depolarizing current becomes more confined to the cell and there
is less electrical load and less current flow to the neighboring non-excited cells.
15
Figure 2.7: Each gap junction consists of two connexons. Connexons are made of six
proteins called connexins; Adapted under a WikiMedia public domain license from original
work by Mariana Ruiz; Online: https://goo.gl/zQqdmn
2.2.3 Excitation-Contraction coupling
The process of synchronization of mycocyte electrical excitation with the mechanical
contraction of the cardiac muscle is called excitation-contraction coupling (ECC). A
synchronized mechanical contraction is essential to pump the blood with a timely
and maintained pressure. Ca2+ is the main activator of myofilaments causing myocyte contraction. Therefore, Ca2+ dynamics play an important role in ECC. The
main structures involved in the ECC are:
(1) sarcomere, which is a serial unit of
myofilaments that form an extensive myofibrillar structure, and is responsible for the
mechanical contraction and tension development; (2) sarcoplasmic reticulum (SR),
which is an internal storage of Ca2+ ions. During the diastole, Ca2+ is stored in
the SR; (3) T-tubules, which are deep invaginations of the sarcolemma and contain
16
the L-type calcium channels and (4) mitochondria, which provides the adenosine
triphosphate (ATP) which is being used as an energy pack for contraction and other
metabolic needs of cardiac myocytes.
Calcium enters the cell during the cardiac action potential mainly through the Ltype calcium channels in T-tubules responsible for the plateau phase of the AP. Entry
of Ca2+ increases the intracellular Ca2+ concentration ([Ca2+ ]i ) that activates ryanodine receptors (RyR), which triggers the release of Ca2+ from the SR. This process is
known as calcium induced calcium release (CICR) and results in a quick rise of [Ca2+ ]i
. The free Ca2+ ions in the cytosol bind to the myofilament protein which reults in the
cell contraction. Relaxation occurs when [Ca2+ ]i declines, which allows Ca2+ ions to
dissociate from myofilament proteins (troponin C). Cytosolic Ca2+ ions are extruded
in four different ways:
(1) almost 80% of the cytosolic Ca2+ is taken up by the
SR [10] through Ca2+ -ATPase channel (Jup ); (2) sarcolemmal Na+ /Ca2+ exchange
current (NCX); (3) sarcolemmal Ca2+ -ATPase and (4) mitochondrial Ca2+ uniport
as shown in Fig. 2.8.
2.2.4 Electrocardiogram (ECG)
The electrical conduction in the whole heart can be measured on the body surface in
the form of the electrocardiogram (ECG). The propagation of the extracellular current
in the heart generates an electrical field which can be measured by an electrode placed
in the vicinity of the heart. The electrode will measure an attenuated and spatially
averaged distribution of potentials generated by the current flow through the tissue
in the torso until they reach the surface.
An ECG is a routine clinical test that shows how fast the heart is beating, if the
rhythm is steady or irregular, and the strength and timing of electrical signals as they
17
Figure 2.8: Ca2+ enters the cell mainly through L-type Ca2+ channels which are densely
embedded in T-tubules. Ryanodine receptor channels ease the release of Ca2+ from the SR
in response to increased [Ca2+ ]i . Different pumps and exchangers extrude Ca2+ from the
intracellular space. Reprinted by permission from [10].
pass through each part of the heart. ECG results are used to detect and study many
health problems such as cardiac arrhythmias, heart attack, and heart failure.
A schematic of one cardiac cycle of an idealized ECG is shown in Figure 2.9, in
which each distinct waveform is labeled as P, Q, R, S, or T. Each waveform relates
to the activation or repolarization of some part of the heart. The P wave is caused
by the spreading activation over the atria, while the Q, R, and S waves are caused
by the activation of the ventricles. The T wave is a result of the repolarization of the
ventricles. The U wave is a small deflection immediately after the T wave, usually in
the same direction as the T wave.
18
R
T
P
U
Q S
Figure 2.9: The schematic representation of a human ECG. Individual waveforms are
indicated by their associated names.
2.3 Arrhythmia and Fibrillation
Arrhythmia is defined as an abnormal pattern of cardiac electrical activity. These
abnormal activities can occur in different regions of the heart in various forms. Depending on the region of the arrhythmia, some types of arrhythmia are less fatal than
others. For instance, disorderly atrial activation can result in irregular ventricular
activation due to the electrical separation of the chambers and the delay of the AV
node. In contrast, even small arrhythmogenic activities in ventricles can lead to more
dangerous irregularities as they can alter or suppress the blood delivery of the heart.
2.3.1 Types of arrhythmia
A successful heartbeat requires both impulse generation and propagation to be performed flawlessly. Abnormalities in either will result in an irregular heartbeat or
dysrhythmia. Abnormal impulse generation and abnormal impulse conduction can
result in irregular heart rhythms and therefore arrhythmia.
Arrhythmia can be classified by the heart rate. If the heart rate is lower than the
normal heartbeat, the arrhythmia is called bradycardia and if the heart rate is faster
19
than normal it is called tachycardia. Bradycardia may be due to slow SA firing rate
(sinus bradycardia), or by damaged electrical pathways from atria to ventricles (AV
node block). On the other hand, tachycardia mostly results from additional abnormal
impulses to the normal sinus rhythm. The main mechanisms behind abnormal impulse
generation are: 1) automaticity and 2) triggered beats.
Automaticity is known as the mechanism of a myocyte firing action potential on
its own. Every impulse that originates outside of the sinus node is called an ectopic
focus. An ectopic focus, if successful to propagate, may cause a single premature
beat or, if it fires at a higher rate than sinus rhythm, can produce abnormal rhythms
(ectopic beats). Ectopic beats produced in the atria are less likely to be a dangerous
arrhythmia but can reduce the cardiac pumping ability and efficiency.
Triggered beats mainly happen due to abnormal depolarization of cardiac myocytes that can interrupt phase 2, phase 3, and phase 4 of the action potential and
are known as afterdepolarizations. Deficiency in Ca2+ or Na+ channels can cause
secondary depolarization of the action potential in phases 2 and 3 respectively, which
is called an early afterdepolarization (EAD) [11]. If a secondary depolarization begins during phase 4 of the action potential just before repolarization is completed,
it is called a delayed afterdepolarization (DAD)[12]. SR Ca2+ overload may cause
spontaneous Ca2+ release during repolarization, resulting in high [Ca2+ ]i . Released
Ca2+ exits through Na+ /Ca2+ exchanger (NCX) which has a net depolarizing current
causing DADs.
Abnormal impulse conduction is another cause of arrhythmia and can be divided
into two possible categories: 1) conduction block, and 2) reentry (discussed in detail
in next section). SA node block, AV node block, and bundle branch block are different
arrhythmia caused by conduction block.
20
Fibrillation is a situation when an entire cardiac chamber is involved in a single
or multiple electrophysiological abnormalities and therefore trembles with irregular
chaotic electrical impulses. Fibrillation can occur in atria (atrial fibrillation—AF) or
ventricles (ventricular fibrillation—VF). AF is not considered a medical emergency
while VF is an imminent life-threatening situation and if left untreated can lead to
death within minutes.
2.3.2 Reentry
The electrical excitation generated at the SA node propagates through the heart
surface in an orderly pattern and then vanishes; i.e. every excitation is initiated and
generated by an impulse from the SA node in normal sinus rhythm. However, the
activation wavefront may travel around a physical obstacle or unexcitable tissue in a
self sustaining fashion instead of dying down. This robust recurring activity, which
can be the source of abnormal cardiac electrical activities and arrhythmia, is known
as reentry. This reentrant waveform continues to excite the heart because it always
encounters excitable tissue in a loop.
Reentry can be divided into two categories: anatomical and functional reentry.
The anatomically reentrant wavefrom travels around an unexcitable tissue (such as
dead tissue) or an object of reduced excitability. Figure 2.10 shows an anatomical
reentry. When conduction blocks in one direction around an anatomical obstacle (unidirectional block), the activation waveform rotates around the block and establishes
a macroscopic reentry.
Functional reentry is in the form of a spiral wave that does not rotate around an
obstacle, but propagates around the whole region of tissue based on the differences
in the refractory properties of excitable tissue. The most common cause of functional
21
(a)
(b)
Figure 2.10: Schematic representation of an anatomical reentry; the anatomical obstacle
is shown as the solid black circle. (a) Activation initiates from the red dot and propagates
in both directions. Gray area shows a unidirectional block which prevents the activation
to propagate counterclockwise but allows propagation in opposite direction. (b) Reentry
propagates clockwise and sustained.
reentry is the gradient in refractoriness in a cardiac region. As shown in Fig. 2.11, in
order to simulate a reentrant activity, a plane wave is initiated by stimulating along
the top part of the 2D sheet (S1). As S1 propagates downward through the tissue and
repolarization wave vanishes in the upper part, the second stimulus (S2) is applied at
the top right corner of the tissue. This results in propagation to the left side of the
tissue but not downward because the upper side is either excitable or in the relative
refractory state while the lower part is unexcitable and is in the absolute refractory
state. The wavefront then rotates clockwise around a point near the center of the
tissue (varies based on the timing difference between S1 and S2, stimulus strength, etc)
as activation gradually propagates to the areas that recovering from repolarization
and becoming excitable. It has to be noted that the S2 has to be applied at a certain
22
time interval after S1 to generate the reentry. This interval is called the window of
vulnerability. This is explained in more detail in section 5.2.7. This spiral wave can
be the origin of many abnormal electrical activities such as fibrillation.
S1
S2
5ms
30ms
32ms
34ms
40ms
45ms
Figure 2.11: Simulation of functional reentry using S1-S2 stimulation; Reentry is initiated
in a 2D 1cm × 1cm tissue of rat ventricular myocyte [51]. S2 is applied in the top right
corner. A sustained sprial wave is generated as the activation waveform propagates around
the tissue.
The concept of the wavelength of a circular impulse was introduced by Smeets
and his colleagues in 1986 [13]. It is defined as the product of conduction velocity
(CV) of the circulating wavefront and the effective refractory period of the tissue
in which the reentry is propagating. Refractory period sometimes is approximated
by the action potential duration. Wavelength quantifies the distance the wavefront
travels during the refractory period. For reentry to occur and sustain, the wavelength
23
of the reentrant wavefront must be shorter than the length of the effective reentry
pathway. That is, the time it takes for the impulse to travel around in one cycle must
be longer than the refractory period to provide the myocardium sufficient time to
recover excitability. In this work, functional reentry is the main type of reentry being
discussed. The word reentry refers to functional reentry unless otherwise specified.
2.3.3 Gap junctions and arrhythmias
Gap junction coupling plays an important role in the arrhythmogenic characteristics
of cardiac tissue, mainly through three different mechanisms: 1) conduction velocity,
2) conduction block, and 3) source-sink relations.
As explained above, the wavelength (λ) is an important factor for sustaining
reentry which is a product of conduction velocity (CV) and refractory period approximated by action potential duration (APD):
λ = CV × APD
(2.1)
Reduced λ increases the chances of reentrant activities as shorter wavelength increases the recovery time in a given path length. Therefore, action potential shortening and reduced CV result in more vulnerability to reentrant activities. Conditions
such as gap junction uncoupling, which reduces the CV, increases the likelihood of
arrhythmia.
Conduction block itself, if it happens in a conduction system, can be an arrhythmogenic phenomenon. Conduction block is known to happen mostly in the tissue
boundary regions where CV heterogeneity exists such as SA and AV nodes. However, as explained in section 2.3.2, one of the basic requirements for initiation of an
anatomical reentry is the formation of conduction block. In the regions with more
24
homogeneous CV, conduction block may occur due to changes in ionic currents or
gap junction remodelling which leads to longer APD and reduced CV. Hence, heterogeneities of CV or APD can be pathological and increase the vulnerability to
arrhythmia in the corresponding substrate.
Initiation of the reentry also plays a key role in vulnerability to arrhythmia as
well as reentry sustainability. As explained before, EADs and DADs are arrhythmogenic triggered activities that can lead to ectopic beats. The occurrence of EAD and
DAD does not always result in reentry. However, they can generate premature beats
(commonly known as premature ventricular complexes—PVCs) if they can propagate
into a large number of myocytes. Therefore, afterdepolarizations are arrhythmogenic
activities not only because they provide regions with APD heterogeneity in the tissue,
but also because they develop PVCs that can propagate into the tissue and cause a
reentry. Considering an EAD in a region of tissue as a source of the electrical current
and the neighbouring region as a sink of that current, certain levels of coupling are
required for current propagation. These are known as source-sink relationships. It is
known that normal levels of coupling result in synchronization of the tissue with EAD
without developing PVCs and APD heterogeneity [14]. On the other hand, reduced
coupling can allow a smaller size of tissue exhibiting an EAD to generate a PVC and
increases the likelihood of arrhythmia.
2.4 Diabetes and the Heart
Diabetes Mellitus (DM), which is also commonly known as diabetes, is a syndrome of
dysfunctional metabolism resulting in abnormally high levels of glucose in the blood
(hyperglycemia). The levels of blood glucose in the body are controlled mainly by
25
insulin which is secreted by a group of beta cells in the pancreas.
2.4.1 Types of Diabetes
If the pancreas fails to produce enough insulin, the DM is called type 1 diabetes. The
patients then require using insulin replacement. Type 2 diabetes results from the
body developing resistance to the effects of insulin. Both types result in increased
blood sugar level which if left untreated can cause long term acute complications
such as cardiovascular diseases, stroke, kidney failure, and damage to the eyes. In
this study we mainly focus on type 1 diabetes which is an autoimmune disease that
results in the destruction of the insulin producing beta cells in the pancreas [15].
2.4.2 Diabetic Heart
Complications related to DM affect many organ systems and are responsible for the
majority of morbidities and mortalities associated with the disease. These complications can be divided into vascular and nonvascular, and are similar for type 1 and type
2 DM. The vascular complications of DM are further subdivided into microvascular
(retinopathy, neuropathy, nephropathy) and macrovascular complications (coronary
heart disease—CHD, peripheral arterial disease—PAD, and stroke). Microvascular
complications are diabetes-specific, whereas macrovascular complications are similar
to those in nondiabetics but occur at greater frequency in individuals with diabetes.
Nonvascular complications include gastroparesis, infections, skin changes, and hearing
loss [16].
Cardiovascular diseases (CVD) are increased in individuals with type 1 or type
2 DM. The Framingham Heart Study revealed a one- to fivefold risk increase in
PAD, coronary artery disease, myocardial infarction (MI), and congestive heart fail-
26
ure (CHF) in DM. Diabetes can affect cardiac structure and ventricular function, a
condition which is called diabetic cardiomyopathy. This makes diabetes a risk factor
for developing systolic and diastolic dysfunction and heart failure. Heart failure is a
common disorder with high rates of mortality which is widespread in many patients
with diabetes mellitus.
In addition, the prognosis for individuals with diabetes who have coronary artery
disease or MI is worse than for nondiabetics. CHD is more likely to involve multiple vessels in individuals with DM. In addition to CHD, cerebrovascular disease is
increased in individuals with DM (threefold increase in stroke). DM is responsible
for increased atherosclerosis in aorta and coronary arteries which increases the risk of
myocardial infarction and stroke. Thus, after checking for all known cardiovascular
risk factors, type 2 DM increases the cardiovascular death rate twofold in men and
fourfold in women [16]. The American Heart Association has designated DM as a
“CHD risk equivalent,” and type 2 DM patients without a prior MI have a similar risk
for coronary artery-related events as nondiabetic individuals who have had a prior
MI.
The increase in cardiovascular morbidity and mortality rates in diabetes appears
to relate to the synergism of hyperglycemia with other cardiovascular risk factors.
Risk factors for macrovascular disease in diabetic individuals include dyslipidemia,
hypertension, obesity, reduced physical activity, and cigarette smoking [16]. Dyslipidemia is an abnormal amount of lipids in the blood which mostly appears as an
elevation of lipids in the blood in developed countries (hyperlipidemia).
27
2.4.3 Electrophysiological Complications of Diabetes
2.4.3.1 ECG abnormalities
Prolongation of the QT interval in the ECG is one of the most common electrophysiological effects of type 1 diabetes [17]. QT interval mainly represents the APD of
ventricular myocytes and therefore, QT prolongation corresponds to the prolongation of APD. T wave abnormalities and QRS prolongation are also suggested in other
studies [18, 19]. These abnormalities are partially due to reduced impulse propagation
conduction velocity.
2.4.3.2 Ion channel remodelling
It has been shown in many studies that the APD is prolonged in diabetic hearts.
The prolongation of AP is mainly due to reduced outward repolarization currents
such as calcium independent transient outward potassium current (Ito ), rapid and
slow delayed rectifier currents (IKr and IKs respectively). It has been shown that the
expression of corresponding potassium channel subunits is reduced in the diabetic
cardiac tissue [20]. Smaller amount of Ito results in delayed early repolarization phase
and reduced IKr
and IKs results in prolonged repolarization phase of the action
potential.
2.4.3.3 Connexin lateralization
Alterations in GJ expression as well as GJ localization lead to impaired impulse
conduction. Slowed CV reflects in broadening of QRS complex of the ECG, results
in disorderly ventricular contraction and forms a potential arrhythmogenic substrate.
Nygren et al. [21] obtained the organization of Cx43—the main connexin protein in ventricular myocytes—and compared streptozotocin-induced diabetic (STZdiabetic) with healthy rat. Total expression of Cx43 was not altered in diabetic rats
28
as depicted in Fig.2.12. However, immunofluoresence labeling of Cx43 confirmed that
the organization of Cx43 was significantly altered 7 days after injection of STZ. These
alterations not only include a reduction in the amount of Cx43 at the intercalated
discs (Fig.2.13), but also a redistribution of Cx43 from the ends of the cell to the
cell sides which is known as “connexin lateralization” (illustrated in Fig.2.13 and
Fig.2.14 respectively)[21]. Nygren et al. showed that Cx43 is dissociated from other
major components of gap junctions suggesting that the lateralization results in nonfunctional junctions. This reduces the conductivity of GJs and altered anisotropy of
the tissue which is also a cause of QT prolongation.
(A)
(B)
Figure 2.12: Quantification of Cx43 in STZ-diabetic and healthy rat; Western blot of
ventricular cardiac myocyte for control and diabetic rats(A) and its analysis (B) is shown.
The releative density of the Cx43 in control and diabetic samples were not significantly
different from one another. Reprinted by permission from [21].
Lateralization of Cx43 is also a common feature of surviving myocytes around
the infarct region in human ventricle [22]. A similar redistribution has been observed
in some rat models of ventricular hypertrophy and has been shown to be correlated
with reduced longitudinal conduction velocity [23]. At four days post-infarction in a
dog model, lateralized Cx43 correlated spatially with re-entrant electrophysiological
29
Figure 2.13: The fraction of immunofluorescence labelled Cx43 associated with intercalated
discs (ICD) and that associated with lateralized Cx43 for both control and STZ-diabetic
rat; The fraction of lateralized Cx43 was significantly higher in the STZ-diabetic myocytes.
Reprinted by permission from [21].
activities [24].
In addition to observations made at the infarct border zone, lateralization has been
reported in end-stage human heart failure [25] and in the ventricles of patients with
compensated hypertrophy due to valvular aortic stenosis (a disease in which the aortic
valve narrows and prevents the valve from fully opening [26]). Cx43 is particularly
redistributed in hypertrophic cardiomyopathy, which is the most common cause of
sudden cardiac death in young adults due to cardiac arrhythmia [9].
Another different form of gap junction remodelling had been observed in patients
with ischaemic heart disease. When the blood flow to the heart is reduced, some
regions of ventricular myocardium lose their ability to contract properly, but are able
to retain their contractile functionality if the blood flow is restored. These regions are
called “hibernating myocardium”. In hibernating myocardium, the overall amount of
30
Figure 2.14: Analysis of Cx43 lateralization; immunofluorescence images of an isolated
ventricular myocyte from STZ-diabetic rat heart (left) and healthy rat heart (right); The
images show Cx43 migrated from the cell ends to the cell sides in the diabetic myocyte.
Reprinted by permission from [21].
Cx43 per intercalated disc is reduced compared to the normally perfused myocardial
regions of the same heart [27]. Apart from disturbances in gap junction remodelling
discussed above, connexin expression may be altered in human heart disease. Several
studies [28, 29] also demonstrated reduced Cx43 transcript and protein levels in the
left ventricles of transplant patients with congestive heart failure.
2.4.3.4 Calcium abnormalities
Calcium is the main ionic regulator in excitation-contraction coupling and is essential
for normal cardiac function. High concentration of Ca2+ ion can be arrhythmogenic
as explained in Sections 2.2.3 and 2.3.1, where it is shown that activities of all of
the currents, exchangers, and pumps involved in the Ca2+ dynamics and excitation
contraction coupling (ECC) such as NCX, Jup , SERCA, and RyR are reduced, which
31
is explained in detail in Sections 5.2.2 to 5.2.4. Some of these alterations result
in reduced [Ca2+ ]i while the others cause increased [Ca2+ ]i . The overall effect is
increased overload of cytosolic calcium, impaired relaxation and diastolic dysfunction.
32
Chapter 3
Biophysical Mechanisms
This chapter briefly reviews the basics of cellular electrophysiology, the mathematical
modelling techniques used in cellular electrophysiology, and the numerical methods to
overcome the complexity of the mathematical models without too much simplification.
3.1 Cell Membrane
The cellular membrane is a lipid bilayer in which proteins are inserted. These proteinlined pores are called ionic channels, which allow the flow of specific ions, mainly
N a+ , K + , Cl− , and Ca2+ . The membrane does not allow the ions to flow freely
and maintains concentration differences of these ions across the membrane. The
concentration gradients of ions produce a potential difference across the membrane,
the transmembrane potential, drives the ionic currents.
3.1.1 The Nernst-Planck Equation
Ions move across the membrane for two reasons. The concentration gradients itself
causes the diffusion flux Jdiff which satisfies Fick’s law :
Jdiff = −D∇c,
where D is the diffusion coefficient (cm2 s−1 ) and c is the concentration (mol cm−3 ).
The electric field generated by the concentration gradients also causes the electric
33
flux of ions Jelect which satisfies Planck’s equation:
Jelect = −
z
µc∇u,
|z|
2
−1 −1
where u is the electric potential (V ),
 µ is the mobility of the ion (cm V s ), z is


+1, for positive ions
z
the valence of the ion so that |z| =
.


−1, for negative ions.
The total ionic flux J can be calculated by adding the electric flux and diffusion
flux:
J = Jdiff + Jelect = −D∇c −
z
µc∇u.
|z|
(3.1)
Considering Einstein’s formula, we can relate the diffusion coefficient D and ion mobility µ via:
D=
µRT
,
|z|F
(3.2)
where R is the universal gas constant (8.314 J/(K.mol)), T is the absolute temperature
(K), and F is the Faraday’s constant (9.648 × 104 C/mol). Hence substituting 3.2 in
3.1 we can obtain the Nernst-Planck equation:
zF
J = −D ∇c +
c∇u .
RT
(3.3)
3.1.2 Nernst Equilibrium Potential
We can assume that the electric potential only depends on x across the membrane
from intracellular (x = 0) to extracellular (x = L) and the diffusion coefficient is
constant. Therefore we can re-write as:
dc
zF du
J
(x) +
(x)c(x) +
=0
dx
RT dx
D
34
(3.4)
Equation 3.4 is a linear differential equation for c(x) and the solution can be found
as:
J
zF
u(x) − u(0)
c(0) −
c(x) = exp −
RT
D
Z
x
exp
0
zF
(u(s) − u(0)) ds
(3.5)
RT
At thermodynamical equilibrium, each local process and its reverse proceed at the
same rate, therefore the flux across the membrane of the generic ion K with valence
z is zero (J = 0). The solution of the Nernst-Planck equation then becomes:
zF
u(x) − u(0) c(0),
c(x) = exp −
RT
from which it follows that, for x = L,
log
c(L) c(0)
=−
zF
(u(L) − u(0)).
RT
Denoting i and e to show intra- and extracellular spaces respectively, we can obtain
the Nernst equilibrium potential,
c RT
i
vK := ui − ue = −
log
.
zF
ce
(3.6)
Table 3.1 shows the typical values of extra- and intracellular concentrations and
Nernst potential values of a ventricular myocytes.
3.1.3 Electrical Model of Cell Membrane
The cell membrane separates ions (electrical charges) between intracellular and extracellular medium. Therefore, it can be modelled as a capacitor with lipid bilayer
dielectric (Cm ≈ 1µF/cm2 ). Each ionic channel can also be modelled as a branch with
variable conductance in series with the Nernst equilibrium potential of that specific
ion. Different ionic channels are connected to each other in parallel between intracellular and extracellular media. Figure 3.1 shows this configuration of membrane
behaviour, which is known as a parallel conductance model.
35
Extracellular
Intracellular
Nernst
concentration (mM)
concentration (mM)
potential (mV)
N a+
145
10
60
K+
4.5
140
-95
Ca2 +
1.8
1e-4
130
Cl−
100
5
-80
H+
1e-4
2e-4
-18
Table 3.1: Extra- and intracellular concentrations and Nernst potential for a ventricular
myocyte.
Considering Kirchoff’s current law, the transmembrane current given by sum of
capacitive and ionic currents must be equal to applied current Iapp (or stimulation
current Istim ). Therefore we can write:
Cm
dv
+ Iion = Istim ,
dt
(3.7)
where Iion is the sum of all ionic currents. In order to describe each ionic current we
need to discuss different modelling approaches for these currents.
3.2 Ionic Current Models
In this section we discuss two out of many different mathematical techniques that are
used to model ionic currents through the cellular membrane.
36
Figure 3.1: Electric circuit model of the cellular membrane
3.2.1 Hodgkin & Huxley Model
In 1963, Alan Hodgkin and Andrew Huxley received the Nobel Prize for their experiments on squid giant axon published in 1952. They developed a conceptual model
based on the studies on the squid giant axon and proposed a formalization to mathematically represent the nonlinear dependency of channel conductance on membrane
potential and time. For example in this model, the movement of sodium ions is explained by activation and inactivation gates denoted by m and h respectively. At the
resting membrane potential the sodium channel is in a closed state. The m gate is
closed and the h gate is open. Voltage sensitive gates undergo conformational changes
when the membrane potential changes. As the membrane potential increases, the m
gates rapidly activate and open the sodium channels. The electrochemical gradient
of sodium drives sodium ions to enter the cell. As the m gates open and membrane
potential increases, the h gates begin to close however m gates open more rapidly
than the h gates close. The difference between the rates of opening and closing of two
gates causes the sodium to enter the cell for few milliseconds. During the repolarization phase of the action potential, sodium channels stay inactivated. Near the end of
the repolarization, the negative membrane potential closes the m gates and opens h
37
gates.
The ionic current through a population of ionic channel is generally given in a
unit area of membrane surface and can be modelled as:
IN a = gN a (Vm , t)ψ(Vm )
(3.8)
where gN a (Vm , t) is the proportion of open sodium channels on the membrane and
ψ(Vm ) is the current-voltage relation of a single open sodium channel. There are three
similar activation and one inactivation independent subunits for the sodium channel,
therefore equation 3.8 can be rewritten as:
IN a = GN a m3 h(Vm − EN a )
(3.9)
where GN a and EN a are the maximum conductance and the Nernst potential of
sodium channels respectively, and m and h are the probability of activation and
inactivation gates to be open respectively. For a generic gating variable w, we can
write a first order kinetics equation as:
w∞ (Vm ) − w
∂w
= αw (1 − w) − βw w =
.
∂t
τw (Vm )
Hodgkin and Huxley examined the response of N a+ and K + currents separately
to different membrane voltage protocols and used curve fitting to match their results
with derived exponential equations:
αm =
0.1(25 − vm )
;
e0.1(25−vm ) − 1
vm
αh = 0.07e− 20 ;
vm
βm = 4e− 18
βh =
1
e
30−vm
10
(3.10)
(3.11)
+1
where vm is the difference between Vm and its resting level (i.e. resting potential is
shifted to zero). We can also find the steady state and time constant of each gating
variable from the above equations as
38
αm
;
αm + βm
αh
;
=
αh + βh
m∞ =
τm =
1
αm +βm
(3.12)
h∞
τh =
1
αh +βh
(3.13)
Hodgkin and Huxley followed a similar procedure to develop a model for the K +
current which is the main outward current. The difference between potassium and
sodium models is that the K + channel does not have the inactivation gate. When
the membrane potential increases the K + current gradually rises to its steady state
value without an inactivation mechanism similar to that of the N a+ current. The K +
channels have four activation subunits shown by n so the formulation for IK similarly
is
IK = GK n4 (Vm − EK ),
(3.14)
where GK and EK are the maximum conductance and the Nernst potential of potassium channels respectively. Kinetics of n were calculated by isolating potassium
current from total current and using curve fitting techniques to match the results
when different voltage protocols are applied, resulting in the following equations:
αn =
0.01(10 − vm )
;
e0.1(10−vm ) − 1
αn
n∞ =
;
αn + βn
vm
βn = 0.125e− 80
τn =
1
αn +βn
(3.15)
(3.16)
3.2.2 Markov Models
The Hodgkin-Huxley formalism describes some ionic channel activities clearly and
provides relatively simple models with little computation effort. However, many recent experiments have shown that the Hodgkin-Huxley gating parameters do not
represent specific kinetic states of ion channels and cannot describe various aspects
39
of channel behavior. For example, inactivation of a Na+ channel is more likely when
the channel is open. In other words, inactivation depends on activation and the assumption of independent gating that gives the Hodgkin Huxley conductance m3 h is
not valid. In case of modelling ionic currents with this level of detail, we can use a
Markovian formalism to represent each physical state of a specific channel with one
state of related Markov model.
A Markov model consists of a list of possible states of a system, the possible
transitions between those states, and the rate parameters of those transitions. The
transition rates between Markov states are governed by first order kinetics. Figure
3.2 shows a single ion channel with only one opening gate that results in a two-state
Markov model: open state (O) and closed state (C). Then the governing equations
of the model is:



dC
dt
= −γC + δO


dO
dt
= −δO + γC
O and C denote the probability of the channel to be in open and closed states respectively and hence we can write O + C = 1.
γ
C
δ
O
Figure 3.2: A simple two-state Markov model
Now consider adding an inactivation mechanism to the channel. Depending on
the configuration of the channel, this inactivation state can be modelled differently as
shown in figure 3.3. In the subfigure 3.3(a), the inactivation state I is only accessible
from the open state O while there is a transition to inactivation from closed state
in configuration 3.3(b). Configuration 3.3(c) has two inactivation states shown by I0
and I1 which are reachable from the closed and open state, respectively. This model
40
can explain the slow inactivation state of sodium that can only be accessed while the
activation gate is conducting and the fast inactivation gates are non-conducting.
I
C
O
(a)
C
(b)
I
I0
I1
O
C
O
(c)
Figure 3.3: Different configurations of an ion channel with one activation and one inactivation gate.
Figure 3.4 shows the equivalent Markov model of the Hodgkin-Huxley sodium
channel where αm , βm , αh , and βh explained in section 3.2.1. Inactivation and closed
states are shown by IX and CX respectively where X denotes the number of activation
gates being conductive. For example, I0 is the state where all activation gates are
closed and the inactivation gate is non-conductive. I1 is accessible from I0 when
one activation gate opens. The probability of this transition is 3α since there are
three closed activation gates available to be opened. Similarly, I1 is going to I2 with a
probability of 2α, since one of the activation gates is already open in I1 . C0 is reached
from I0 when inactivation gate opens with probability of αh and all activation gates
are closed. In this configuration the only conducting state is O which is the term m3 h
in equation 3.9.
Each state is the probability of the channel to be in that configuration therefore
they have a value between 0 and 1 and hence the sum of all states is 1 at any given
time. The rate of change in each state can be determined by the difference between
41
3αm
I0
αh
βm
αh
βh
C0
3αm
βm
2αm
I1
2βm
αh
βh
C1
2αm
2βm
αm
I2
I3
3βm
αh
βh
C2
βh
αm
3βm
O
Figure 3.4: Equivalent Markov model of Hodgkin-Huxley sodium current
incoming and outgoing arrows. For example for state O we can write:
dO
= αm C2 + αh I3 − (3βm + βh )O
dt
Another advantage of Markov models becomes evident when a drug or a channel
blocker acts on a specific state of the channel. A new state can be added to the related
Markov model to account for the drug binding to the channel. However, in Markovian
modelling , the price to pay for for the highly detailed description of ionic channels
and other sub-cellular processes is an increase in complexity and computational cost.
3.3 Signal Propagation in Cardiac Tissue
3.3.1 Bidomain Modelling
The bidomain representation of cardiac tissue describes both extra- and intracellular
potential fields (φe and φi respectively) and relates them to membrane behaviors and
transmembrane current density Im .
Consider the equivalent circuit representation of cardiac tissue in one dimension
as shown in figure 3.5. The intracellular space has a conductivity of σi (or resistivity
of ri ) while the extracellular conductivity is σe (or resistivity of re ).
42
re
re
ie
im
−
iion
ic
rm
...
Vm
Cm
−
+
...
Em
+
ri
ri
ii
Figure 3.5: Equivalent bidomain circuit diagram of single cell.
The current density J can be calculated from electrical field E based on Ohm’s
law:
J = σE
(3.17)
where the electric field can be calculated as the negative of the gradient of scalar
potential field φ (E = −∇φ), therefore equation 3.17 becomes
Ji = −σi ∇φi
(3.18)
Je = −σe ∇φe
(3.19)
When there is no stimulation current and if the cardiac cell assumed to be isolated,
any changes in current density in one domain implies a current flow through the cell
membrane into the other domain:
−∇ · Ji = ∇ · Je = βIm
(3.20)
∇ · (σi ∇φi ) = −∇ · (σe ∇φe ) = βIm
(3.21)
where β is surface to volume ratio of the cell membrane.
43
The media are considered to be continuous and material properties are averaged.
The structural features of cell to cell connections are homogenized. By expressing the
tissue properties as continuous we can use numerical methods to discretize domains
and solve the differential equations. Therefore, the conductivities are formalized as
tensors (σ¯e and σ̄i ). If there are any external stimuli applied to extracellular medium
we can rewrite the equations as follows:
∇ · (σ̄i ∇φi ) = βIm
(3.22)
∇ · (σ¯e ∇φe ) = −βIm − Ie
(3.23)
where Ie is external stimulus applied to extracellular medium and Im is calculated as:
Im = Cm
∂Vm
+ Iion (Vm , v).
∂t
(3.24)
In this equation, Iion is a function of membrane potential Vm and all other gating
variables and time which are denoted by v.
This formulation is a set of coupled equations because both extra- and intracellular
potentials have to be calculated simultaneously. These two domains are linear, and
nonlinearity arises from the voltage-current relation of membrane current which is
described by a set of nonlinear ordinary differential equations (ODEs).
Combining the equations 3.22 and 3.23 and considering that Vm = φi − φe will
result in the following equations:
∇ · (σ̄i + σ¯e )∇φe = −∇ · σ̄i ∇Vm − Ie
(3.25)
∇ · (σ̄i ∇Vm ) = −∇ · σ̄i ∇φe + βIm
(3.26)
Equation 3.25 is an elliptic partial differential equation relating membrane potential and stimulation current to extracellular potential. Equation 3.26 is a parabolic
44
partial differential equation relating the extracellular potential and membrane current
to membrane potential. Im (as described in equation 3.24) includes the changes of
membrane potential over the time.
The bidomain equations are necessary when modelling extracellular stimulus and
virtual electrodes.
3.3.2 Monodomain modelling
The elliptic equation is computationally expensive and if the extracellular field is
ignored, the solution of equation 3.25 can be avoided and only the parabolic PDE
needs to be solved. Alternatively if the ratios of the longitudinal and transverse
conductivities in the intracellular and extracellular domains are equal (i.e. σe = kσi ),
then equations 3.22 and 3.23 can be combined to obtain single equation:
1
∇ · σ̄i ∇Vm = (1 + )βIm
k
(3.27)
By replacing the intracellular conductivity tensor with the monodomain conductivity tensor (i.e. σ̄m = σ̄i (σ̄i + σ̄e )−1 σ̄e ), the monodomain equation is obtained as
∇ · σ̄m ∇Vm = βIm
(3.28)
which is equivalent to Equation 3.26 when φe is ignored.
Monodomain equations are less computationally expensive and are very fast to
solve comparing to bidomain equations. However, the monodomain model generally cannot include external stimulus (except when there is linear relation between
extracellular and intracellular conductivities) and thus cannot be used to describe
the response to an electric shock. In this thesis, a monodomain model was used
throughout.
45
3.4 Numerical Methods
3.4.1 Euler’s method
Each dynamic system consists of state variables that describe the mathematical state
of the system. Solving a system of differential equations is updating a set of state
variables at a specific time instance to the their values at the next point of time
denoted by xn and xn+1 respectively. The time difference between two consecutive
time instances (n and n + 1) is denoted by ∆t.
Explicit numerical methods compute the next value of a state variable based on
the current values. For example if a dynamic system is defined as:
∂x
= f (x),
∂t
(3.29)
then the explicit forward Euler method would approximate the next value of x as:
xn+1 = xn + ∆t · f (xn ).
(3.30)
On the other hand, the implicit backward Euler methods include xn+1 in the
formulation and the discretization of the system 3.29 will be:
xn+1 = xn + ∆t · f (xn+1 ).
(3.31)
The explicit method is easy to solve because it does not require any equations to
update xn+1 . However, the use of explicit methods requires impractically small time
steps to be stable and convergent specially when solving stiff dynamic systems. A
dynamic system is called stiff when the system has a very fast dynamic and a slow
dynamic. Therefore, the numerical methods for solving the stiff system requires an
extremely small step size in order to have a stable solution. In contrast, implicit
46
methods are unconditionally stable for PDEs used in cardiac modelling but they are
more time consuming since equation 3.31 needs to be solved for each iteration.
For example, consider a Hodgkin-Huxley gating variable ζ for ion current dynamics:
ζ∞ − ζ
∂ζ
=
∂t
τζ
At a given time n, the forward Euler method would approximate the next value of ζ
as:
ζn+1 = ζn + ∆t
ζ − ζ ∂ζn
∞
n
= ζn + ∆t
.
∂t
τζ
The implicit backward Euler method would use:
ζn+1 = ζn + ∆t
ζ − ζ ζ − ζ ∂ζn+1
∞
n+1
∞
n
= ζn + ∆t
= ζn + ∆t
.
∂t
τζ
τζ + ∆t
If the rate of change depends on other state variables rather than ζ then this
method becomes noticeably more complicated and a set of equations are required to
be solved simultaneously. Both forward and backward Euler methods are first order
accurate in time, meaning that the error of approximations are subject to error in
order of ∆t. This is very significant when large time steps are used.
Note that ζ∞ and τζ are functions of Vm and considered to be constant in an
interval of a time step. This assumption is very common and well suited in biophysical
solutions. If Vm is considered to be constant in a time step, then the solution to
the ordinary differential equation (ODE) of m can be approximated with a simple
exponential function varying from ζn to ζ∞ by the time constant τζ :
ζn+1 = ζ∞ − ζ∞ − ζn e−∆t/τζ
(3.32)
This solution is known as Rush-Larsen method and popularly used in biophysical
phenomena, especially in gating variables of cardiac and neural cells. This method is
47
simple to implement and produces solutions as accurate as those produced via more
expensive techniques [30].
Sometimes additional accuracy can be obtained by combining both forward and
backward Euler methods, i.e.,
ζn+1 = ζn +
∆t h ∂ζn + ∂ζn+1 i
2
∂t
(3.33)
This approach, known as Crank-Nicolson method, is widely used in spatial problems. Consider the diffusion equation which is a parabolic PDE as follows,
!
∂u
∂
∂u
=
D
∂t
∂x
∂x
(3.34)
where D is the diffusion constant. By applying the Crank-Nicolson method we have:
n+1
n+1
n+1
un+1
− unj
D h (uj+1 − 2uj + uj−1 ) + (unj+1 − 2unj + unj−1 ) i
j
=
.
∆t
2
(∆x)2
(3.35)
This model is second order accurate in time and is stable for any ∆t.
3.4.2 Finite Element Method
Finite Element Method is a numerical technique to solve boundary value problems
(BVPs) for partial differential equations. This method involves five main steps:
1) dividing the whole domain (solution region) into a finite number of elements,
2) finding related equations for a typical element, 3) assembling all elements together,
4) applying boundary conditions, and 5) compute the solution of resultant system
of equations.
As an example, consider we want to solve Poisson’s equation to calculate the
potential distribution V (x, y) in a connected open region Ω in the (x, y) plane with
48
Figure 3.6: A solution region and its finite element discretization. Region Ω is divided
into four elements shown by circled numbers. Boundary conditions on ∂Ω must satisfy on
the approximated boundary.
boundary conditions on ∂Ω:


 ∇2 V = f (x, y) on Ω,

 V (x, y) = 0
(3.36)
in ∂Ω.
The solution region is divided into a number of finite elements as illustrated in figure
3.6. Here all elements are considered to be triangles which is a practical approach
for the ease of computations but it is also possible to have different shape elements
such as quadrilaterals, hexagons, etc. An approximation of the potential on the whole
surface is given by:
V (x, y) =
N
X
Ve (x, y)
(3.37)
e=1
where Ve is the potential within element e and N is the number of elements. Ve
can be approximated using basis functions which are called element shape function.
Polynomial approximations are used as basis functions to interpolate the potential
49
Figure 3.7: A triangular element used in FEM calculations. Local nodes are numbered as
1, 2, and 3.
within element e. The most common polynomial function for a triangle element is:
Ve (x, y) = a + bx + cy
(3.38)
where a, b, and c are related to the geometry of the element and nodal potentials.
Consider a typical triangular element as shown in figure 3.7. Potentials at each local
node (Ve1 ,Ve2 , and Ve3 ), can be calculated using equation 3.38 as follows:
  
 
Ve1  1 x1 y1  a
  
 
V  = 1 x y   b 
2
2  
 e2  
  
 
Ve3
1 x3 y3
c
(3.39)
If we solve this equation for a, b, and c in terms of coordinates of local nodes, then
we can rewrite equation 3.38 as follows:
Ve (x, y) =
3
X
i=1
50
αei (x, y)Vei
(3.40)
Similarly the source term f (x, y) in equation 3.36can be written as:
f (x, y) =
3
X
αei (x, y)fei
(3.41)
i=1
where αei are the shape functions considered as a set of basis function for interpolation.
Each αei is 1 for the corresponding local node i, and 0 at the other two local nodes
and varies linearly between:
i
1 h
(xe2 ye3 − xe3 ye2 ) + (ye2 − ye3 )x + (xe3 − xe2 )y
2A
i
1 h
=
(xe3 ye1 − xe1 ye3 ) + (ye3 − ye1 )x + (xe1 − xe3 )y
2A
i
1 h
(xe1 ye2 − xe2 ye1 ) + (ye1 − ye2 )x + (xe2 − xe1 )y
=
2A
αe1 =
(3.42)
αe2
(3.43)
αe3
(3.44)
where A is the area of element e. Note that the above equations are equivalent to
equation 3.39. Equations 3.40 and 3.41 give the potentials and sources at any point
within each element considering that the potentials and sources are known at all
vertices.
The functional form for the potential energy in the element e is given by:
Z h
i
1
2
(3.45)
F (Ve ) =
|∇V | + 2fe Ve dS
2 Ω
The Ve that minimizes F is the approximate solution of Poisson’s equation. Substituting equation 3.40 and 3.41 results in:
Z
Z
3
3
3 X
3
X
1 XX
F (Ve ) =
Vei
∇αi .∇αj dS Vej +
Vei
αi αj dS fej
2 i=1 j=1
Ω
Ω
i=1 j=1
(3.46)
which can be written in matrix form as:
1
F (Ve ) = [Ve ]T [C (e) ][Ve ] + [Ve ]T [M (e) ][fe ]
2
(3.47)
where C (e) and M (e) are the local stiffness and mass matrices of element e respectively.
The elements of these matrices which represent the coupling between the nodes of i
51
and j of element e can be calculated as:
Z
(e)
Ci,j =
∇αi .∇αj dS
Ω Z
(e)
αi αj dS
Mi,j =
(3.48)
(3.49)
Ω
The final step is to use each local 3 × 3 stiffness and mass matrices calculated
above (C (e) and M (e) ) and assemble them to obtain global equation
1
F (V ) = [V ]T [C][V ] + [V ]T [M ][f ].
2
(3.50)
In this equation, each index i relates to the node i in the global numbering scheme
and not element-wise.
In large problems, such as a discretized cardiac geometry, this results into a huge
coefficient matrix [C] which is solved by iterative methods. The coefficient matrix [C]
however is symmetrical and sparse since many nodes have no interaction with each
other and the corresponding entry of matrix is zero.
The method above, where F (V ) is minimized, is known as the Ritz variational formulation. In practice, a simpler form based on Galerkin’s weighted residual method,
is used [31]. First, given Poisson’s problem, it is assumed that V and f can be approximated by linear combinations of N basis functions αi , chosen in a similar manner as
the element shape functions discussed above. Both sides of the equation can be multiplied by some arbitrary weighting function and integrated over the spatial domain
to obtain a new, equivalent equation; in Galerkin’s method, the N basis functions are
thus employed to generate new equations equivalent to the original problem:
Z
2
−
Z
αj (x, y)∇ V (x, y)dS =
ZΩ
∇αj (x, y).∇V (x, y) =
Ω
αj (x, y)f (x, y)dS
j = 1, 2, . . . , N
(3.51)
αj (x, y)f (x, y)dS
j = 1, 2, . . . , N
(3.52)
ZΩ
Ω
52
where the left-hand side has been simplified using integration by parts. When the
approximate forms of V and f are substituted in the equation, results in the following:
N Z
X
i=1
Ω
∇αi ∇αj dS Vi =
N Z
X
i=1
αi αj dS fi
j = 1, 2, . . . , N
(3.53)
Ω
Similar to Equation 3.47, this can be converted to matrix form and solved to obtain
an approximation of the solution V (x, y).
In the tissue simulations of this thesis, a robust tool for performing biophysical
simulations (Cardiac Arrhythmia Research Package—CARP) was used. CARP is
developed by Vigmond et al. [32] and is designed to run in both shared memory and
clustered computing environments. CARP solves bidomain elliptical and parabolic
equations as well as monodomain equations. It consists of several packages like bidomain simulations, ionic model libraries, visualization of structured and non-structured
grids which are dedicated to specific tasks.
2D and 3D simulations in this thesis were solved using monodomain modelling.
Space discretization was implemented by mesher, a simple mesh generator for slabs
and surfaces. Space elements are triangular or quadrilateral in the 2D simulations,
and hexahedral or tetrahedral in the 3D simulations.
53
Chapter 4
Cardiac physiological characteristics measurements
The majority of the contents of the following chapter has been previously
c
c
published in [33] [2012]
IEEE and [34] [2014]
IEEE.
4.1 Chapter Specific Background
Physiological characteristics of heart tissue such as fiber rotation, anisotropy, cell
coupling, and fiber curvature are known to have major effects on wave propagation
patterns in the heart. One way to obtain information about these structural properties is to measure epicardial potential patterns. There have been several studies
designed to determine myocardial anisotropy and conduction velocity based on epicardial potential measurements. While some studies have accounted for the effect of
fiber rotation [35], many have assumed that epicardial conduction patterns directly
reflect epicardial fiber orientation [36, 37]. Known effects of fiber curvature [38] and
transmural fiber rotation on epicardial surface wavefront propagation patterns [39, 40]
have frequently not been accounted for.
Cells are connected internally by gap junctions, which are mainly located at intercalated disks in healthy tissue [21], leading to a higher conductivity in the direction
of myocardial fibers. Therefore, wave propagation is anisotropic and faster in the myocardial fiber direction (longitudinal) than in the direction across the fibers within the
sheet (transverse) and across sheets (transmural). Also, fiber orientation is known to
change from epicardium to endocardium [41, 42]. Therefore, anisotropy and fiber ori54
entation have to be considered in designing measurement approaches for conduction
velocity.
Taccardi et al [43] studied the effect of the myocardial structure on wave propagation patterns in canine left ventricle and showed that the activation isochrones
resulting from epicardial stimuli differed from activation patterns when the wavefront
was limited to only the epicardium. They also showed that both superficial and
transmural fiber directions were reflected in potential distributions [44]. Finally, they
analyzed how features of epicardial potential distribution were affected by pacing site,
pacing depth, and time elapsed after the stimulus.
Nygren et al. [45, 46] used Optical Mapping (OM) to record high resolution optical
maps of activation times and conduction in the mouse heart. They showed that central
stimulation resulted in an elliptical pattern demonstrating that conduction velocities
are anisotropic. Knisely [47] used OM and showed that changes in transmembrane
voltage depend on fiber orientation.
However OM does not measure the transmembrane potential on the surface, but
a weighted average of potential over the depth of the tissue due to light intensity
decay in the tissue. Fluorescent photon scattering is known to distort OM. Bishop
et al. [48] provided a model that accurately synthesizes the 3D photon scattering
effect over the irregular geometry of the rabbit ventricles. They also studied the effect of photon scattering in optical signal distortion during ventricular tachycardia
and defibrillation, and showed that photon scattering causes the difference in amplitude of optically recorded and simulated virtual electrode polarization induced by a
defibrillation-strength shock [49].
55
4.2 Cardiac Optical Mapping
To study the electrical activity and impulse propagation in the heart, it is important
to record the membrane potential by some means. There are different ways to measure
electrical activity of the heart:
A. Patch-clamp is a technique that allows the study of the ionic current or membrane potential of a single or multiple cells or ion channels. Sharp electrodes are also
used to measure the electrical potential inside the cell membrane.
B. Extracellular electrodes can be used to record electrical activity of the heart.
Microelectrodes have high temporal resolution and can be useful to measure the
electric field caused by the electrical activity of the heart [50]. A single electrode
will record information of a single region of the heart and their use for large regions
activity mapping results in the use of a vast number of electrodes. This method
requires complex electrode arrays to achieve good levels of spatial resolution.
C. In order to non-invasively measure the membrane potential of the heart rather
than the electrical field caused by the heart (can be measured by extracellular electrodes), we can use optical mapping. Cardiac optical mapping is an alternative
method that can record surface action potential with higher spatial resolution. A
voltage sensitive dye is perfused in the heart and binds to the cell membrane. The
dye fluoresces based on the membrane potential.
In this thesis, optical mapping (OM) was used to record electrical activity of
the heart from the surface. OM provides a direct membrane potential measurement
with high spatial resolution in return of lower temporal resolution than electrode
measurements.
56
4.2.1 Voltage-sensitive dye
In this study Di-4-ANEPPS was used as the fluorescent dye due to its ability to
follow the voltage changes across the cell membrane on a time scale of milliseconds.
When Di-4-ANEPPS is illuminated at appropriate wavelength (500±25 nm), it emits
a fluorescent signal proportional to the membrane potential of cardiac myocytes.
4.2.2 Imaging system
Figure 4.1 shows the block diagram of the imaging system used in this study. Illumination is provided by a 250 W Quartz Tungsten halogen light source. The light
is reflected off a mirror and filtered with a 500±25 nm band pass filter. The filtered
light (green light) is then reflected off a dichroic mirror to the epicardial surface of
the heart. The fluorescent light (red light) emitted from the cardiac surface is filtered
through the dichroic mirror and then a long pass filter (>590 nm) and reaches the
charge-coupled device (CCD) sensor. The shutter of the camera is controlled by the
acquisition software and opens automatically before image acquisition and closes after recording. The camera is connected to a National Instruments PCI-1422 image
acquisition board.
4.3 Methods
4.3.1 Computational Model
The Pandit [51] mathematical model of rat ventricular myocytes was used as the
base single cell model. 2 × 2 centimeter tissue slabs were created with different thicknesses (1mm, 2mm, 4mm, and 1cm). The myocardial tissue included fiber orientation
that varied continuously and linearly 120 degrees from epicardium to endocardium
57
Figure 4.1: Schematic diagram showing arrangement of the major components of the
imaging system
[52, 53, 54]. Simulations were run assuming a monodomain model using the Cardiac
Arrhythmia Research Package [32] with a time step of 1µs and spatial discretization
step of 100µm. The tissue was stimulated with a 50µA/cm2 current density injected
into a 0.5 × 0.5 × 0.25 mm cube for 5ms at the center of epicardial surface. Simulations were run for all tissue thickness and the membrane potential of each point was
recorded. The transmural conductivity (denoted by gn ) is defined as the conductivity
between different layers of the tissue and is perpendicular to the plane of longitudinal
and transverse conductivity directions. This conductivity affects wave propagation
speed from epicardium to endocardium. Higher transmural conductivity results in
more electrotonic loading from underlying layers of cardiac tissue on the epicardial
surface. Coli Franzone et al. [53] considered transmural conductivity to be equal to
one tenth of the transverse conductivity so the associated propagation velocity (θn )
was in accordance with the findings reported by LeGrice et al. [6]. Therefore, to
58
determine the effect of transmural electrotonic interactions on the epicardial surface,
simulations were run with different transmural conductivities (gn = gt , gt /2, gt /4,
and gt /8).
4.3.2 Data Processing
Activation time was defined for each point as the moment when membrane potential
crossed zero in the action potential upstroke. Isochrones were defined as contour plots
of the activation time which represent the points that have the same activation time.
Since the action potential propagates faster in the fiber direction, isochrones were
expected to have an elliptic shape. A least square error algorithm was implemented
in Matlab to fit ellipses to each isochrone. Coordinates of all the points (X and Y) in
the isochrones are used to find the parameters in 4.1
A(X − h)2 + B(X − h)(Y − k) + C(Y − k)2 = 1
(4.1)
where h and k are the coordinates of the ellipse center. The angle of rotation, along
with the major and minor axes of each ellipse, were determined.
Conduction velocity vectors for each point were calculated using the gradient of
the activation times as described in detail by Morley et al. [55]. Briefly, a plane was
fitted by the least squares method to a 7 × 7 point neighborhood of the activation
times to obtain a smooth approximation to the activation times in the neighborhood.
The direction of the gradient of this approximating plane was taken to be the local
direction of propagation, while the inverse of the magnitude of this gradient was used
as an estimate of the local velocity [55]. This approach is similar to that used by Bayly
et al. [56], with the exception that these authors fitted a quadratic surface, rather
than a linear plane, to the activation times. These methods share the advantage that
59
they factor in activation times over a neighborhood in a least-squares sense, and thus
can be expected to be relatively robust in the presence of measurement noise in a small
number of points. This is in contrast to simpler methods such as the one proposed by
Mazeh et al. [57], which relies on activation time measurements in only four or five
points. Another robust approach for conduction velocity measurement is that of Kay
and Gray [58]. However, this method depends on absolute measurements of membrane
potential and is thus not directly applicable to optical mapping data (which only
provides relative measurements of membrane voltage). Velocity vectors at the apices
of the fitted ellipse (intersection between the long and short axes and the ellipse itself)
were considered to be the longitudinal and transverse conduction velocities, denoted
θl and, θt , respectively in this chapter. The maximum and minimum velocities along
isochrones (not necessarily on the fitted ellipse) were also determined as an alternative
estimate of longitudinal and transverse conduction velocities and are denoted θmax and
θmin , respectively. In all cases, velocities were calculated using the method described
above. The largest conduction velocity vector in any point along the isochrone was
considered to be equal to the longitudinal conduction velocity, θmax . The minimum
conduction velocity in any point along the isochrone was used as an estimate for
transverse propagation velocity, θmin .
4.3.3 Estimation of Epicardial Fiber Orientation
The angle of wave propagation was considered to be the angle of the major axis
of the ellipse relative to the epicardial fiber orientation. This angle provides one
possible estimate of epicardial fiber orientation. Figure 4.2 depicts an ellipse fit to
an isochrone (in 1mm thick tissue) and its major and minor axes. Isochrones in thin
tissues are not completely elliptical, but are “skewed” and have notches along the
60
sides. As a result, the best-fit ellipse is not completely aligned with the perceived
“long axis” of the isochrone, potentially contributing to the error in this estimate
(see Discussion). As an alternative, fiber orientation may be estimated based on
the direction of maximum conduction velocity along a particular isochrone, i.e., at
a particular time post stimulus. In this study, this time was selected to be 20ms to
ensure that measurements were obtained well after the end of the stimulus pulse (to
ensure that they represent conduction rather than the passive response to stimulation)
and before the activation wavefront reached the edge of the tissue slab. In this
alternative measure, fiber direction was considered to be the direction of maximum
conduction velocity along the 20ms isochrones (θmax , as defined above)
Figure 4.2: An isochrone (black solid line) and the corresponding least square fitted ellipse
(dashed line). Major and minor axes are shown with “a” and “b” respectively. The angle
of rotation is φ. The anisotropy ratio is equal to “a/b”.
61
4.3.4 Estimation of Anisotropy Ratio (AR)
The ratio of longitudinal to transverse conduction velocity is a dimensionless parameter called the anisotropy ratio (AR). Three measures of AR were considered in this
study: 1. The anisotropy ratio can be calculated based on the distance traveled by
the activation wavefront, as the ratio of the major to minor axis of the best-fit ellipse
to an isochrone (i.e.,
a
b
in Fig. 4.2). In this chapter, we used the 20ms isochrone
unless otherwise noted. 2. Alternatively, the AR can be estimated as the ratio of
the conduction velocities observed at the apices of the best-fit ellipse, i.e., the AR is
estimated as θl /θt with θl and θt as defined above. 3. Finally, we considered a third
estimate of AR based on the ratio of maximum to minimum conduction velocity along
the 20ms isochrone (θmax /θmin ).
4.3.5 Optical Mapping Model
Fluorescent photon scattering distorts the recordings of cardiac the membrane potential [59, 60]. Excitation light intensity decays as it penetrates through the tissue
and as it goes back out through the tissue to the camera. Due to penetration and
emission, OM does not measure only surface membrane potential. The simplest way
to model and implement this effect is to assume that the excitation light decays exponentially on the way in and that emitted light also decays exponentially on the way
out, modeling the process as the product of two exponentials. After electrical simulations were completed, measured membrane potential with the effect of OM (VOM )
was calculated based on
Rl
VOM =
0
Vm (x, y, z)w(z)dz
Rl
w(z)dz
0
62
(4.2)
where l is the tissue thickness, Vm (x, y, z) is the membrane potential at each point,
z is the depth below the surface, and w(z) is the weighting function which can be
considered as a product of two exponentials for excitation (φex ) and emission lights
(φem ) derived from Baxter et al.[60]:
w(z) = φex (z)φem (z)
(4.3)
φex = 927e−z/0.8mm − 702e−z/0.44mm
(4.4)
φem = e−z/1.34mm
(4.5)
The second term in equation 4.4 accounts for photons leaking out of the tissue near the
surface [60]. Using equations 4.2 to 4.5 on the membrane potential of the tissue, the
measured membrane potential on the epicardium was calculated offline for analysis.
4.3.6 Experimental Methods
All experiments followed the guidelines of the University of Calgary Animal Care and
the Canadian Council for Animal Care and were performed by Marcela Rodriguez.
Rat hearts were isolated as described by Nygren et al. [46]. For OM protocols,
the optical mapping dye Di-4-ANEPPS was added after a 20-minute normalization
period. After normalization, the dye was perfused for 5 minutes, followed by a 10
minute wash out.
Di-4-ANEPPS was diluted from a 10mM stock solution in DMSO (dimethyl sulfoxide) to a 1µM concentration in Krebs-Henseleit buffer solution. To override sinus
activation of the heart pacing with a pulse cycle of 200ms was used. The pacing
current was initiated at 1µA, and increased until the tissue was activated, overriding
sinus rhythm. Once the minimum pacing current needed (threshold) was determined,
the pacing current was set to twice threshold for the remainder of the experiment.
63
The objective is to use a low stimulus to capture a small area of the cardiac tissue so
the isochrones reflect the active propagation in the tissue rather than the passive depolarization caused by the stimulus. Twice threshold was considered large enough to
excite the tissue and small enough not to depolarize a large portion of the heart passively. If the current became insufficient (happened once) to initiate tissue activation
then the current was again increased until activation occurred.
The threshold might change due to the changes in the tissue health and also
due to the changes in the electrode contact to the tissue. The tissue health was
constantly monitored by monitoring the heart temperature, perfusion pressure, and
the electrocardiogram. The electrode contact to the heart surface is more likely to
change in a short time period during the experiments due to the heartbeats.
Six male rats (n=6) were used for the experiments to investigate the rotation of
isochrones qualitatively. The hearts were cut open after the experiments and tissue
thicknesses of left ventricle were measured under the microscope. The average tissue
thickness was 3.5 ± 0.3mm. However this measure is not accurate since the tissue has
cleavages and does not have the same thickness over the heart and left ventricle.
The recorded images were processed off line to obtain the membrane potential of
each pixel. Light intensity mapped to membrane voltage and action potentials were
obtained. Activation time for each pixel was detected and averaged over 10 cycles.
Ellipses were fitted to each isochrone using the same method used for simulation data.
The angle of each ellipse was found and the angle difference of the isochrones was
calculated for each activation time.
64
4.4 Results
4.4.1 Simulation Results
4.4.1.1 Observations based on isochrones
Figure 4.3 shows the contour plot of activation time (isochrones) for different tissue
thicknesses. Direction and speed of wave propagation can be seen from the isochrones.
Fibers on the epicardial surface are oriented in the horizontal direction in all slabs. It
can be seen from Fig. 4.3 that the direction of wave propagation is not aligned with
epicardial fiber orientation. This misalignment is more evident in thinner tissues. It
can also be noted that for a specific thickness, subsequent isochrones are not oriented
in the same direction and the angle of propagation increases with time post-stimulus.
Figure 4.3: Activation time isochrones on the epicardial surface. Fibers are oriented in the
horizontal direction. Isochrones are less aligned with the fiber direction in thinner tissues.
65
Figure 4.4 shows the angle of wave propagation, as determined by the orientation of the long axis of the best-fit ellipse to the 20ms isochrone, for different values
of transmural electrical coupling. The angle of propagation increased with the time
elapsed from the stimulus application. The difference between the angle of propagation and fiber direction was smaller for thicker tissues. Also, as electrical coupling
between layers decreased, this angle discrepancy decreased. It can be noted that for
the tissues with the lowest transmural conductivity (gn = gt /8) the wavefront tended
to propagate in a constant direction (the slope of the blue line is almost zero in all
thicknesses).
Figure 4.4: Angle of wave propagation versus time for different transmural conductivities
and thicknesses. As electrical coupling between layers decreases (gn decreases), impulse
propagation is more aligned with the epicardial fiber orientation. The angle of propagation
is increasing with the time elapsed since the stimulus. This increment is less for thicker
tissues and smaller couplings. Angle of propagation was estimated as the orientation of the
long axis of the best-fit ellipse to the activation isochrone at the time indicated post stimulus.
66
Figure 4.5 shows angle of wave propagation 20 ms after stimulation for different
thicknesses and different transmural conductivities (different “gn /gt ” ratios). Lower
gn /gt ratios resulted in less misalignment of wave propagation with epicardial fiber
orientation for all thicknesses.
Figure 4.6 shows the diagram of measured anisotropy ratio, determined as the
ratio of the long axis to the short axis of the best-fit ellipse, versus tissue thickness
for different transmural conductivities. With thicker slabs, the AR increased and
approached the “true” AR value of tissue with no fiber rotation [61]. It can be noted
from Fig. 4.6 that less transmural conductivity caused less electrical interaction
between the tissue layers. Therefore, measurements in cardiac tissues would be more
accurate under these conditions. However, errors are still substantial for thin tissues.
Figure 4.5: Angle of wave propagation versus tissue thickness for different transmural
conductivities (based on the best-fit ellipse, 20ms after stimulation).
67
Figure 4.6: Anisotropy ratio versus tissue thickness for different transmural conductivities. Anisotropy ratios are measured based on the best-fit ellipse to the activation isochrone
20ms after the stimulation. Measurements are more accurate for thicker tissues. Electrical
coupling between the layers are less effective for thicker tissues.
4.4.1.2 Conduction velocities
Figure 4.7 shows the longitudinal and transverse conduction velocities (θl and θt ) for
different tissue thicknesses and transmural conductivities. Nominal values of longitudinal and transverse conduction velocities are 51 and 17cm/s respectively (θl 3-fold
higher than θt ). These values are calculated for a tissue with no fiber rotation. Estimated longitudinal conduction velocities are smaller than the nominal value of θl
and transverse ones are greater than the true value of θt . As tissues become thicker,
measurements for both longitudinal and transverse velocities approach the true value.
The effect of transmural conductivity on measurements is clearly visible in Fig.
4.7. Measurements from the tissues with smaller transmural conductivity are closer
to the nominal values for both θl and θt .
68
Figure 4.7: Transverse (θt ) and longitudinal (θl ) conduction velocity versus tissue thickness for different transmural to transverse conductivity ratios. As tissues get thicker and
transmural conductivity decreases, measurements approach the nominal conduction velocity
(which is 17 and 51 cm/s for transverse and longitudinal conduction velocity respectively).
θl and θt were obtained at the apices of the 20ms activation isochrones as described in
Section 4.3.
4.4.1.3 Alternative estimates based on conduction velocities
The estimates of epicardial fiber orientation and anisotropy ratio presented in the
previous section were determined based on the best-fit ellipse to the isochrones. To
determine whether the alternative measures based on conduction velocities discussed
in Section 4.3 can be expected to produce more accurate estimates, the same simulation results were subjected to additional analysis. Table 4.1 shows the values of
69
Thickness
AR
1mm
2mm
4mm
1cm
Ellipse
1.7
2.2
2.7
2.9
θl /θt
1
1.8
2.4
2.9
θmax /θmin
2.1
2.4
2.7
2.9
Ellipse
24
16
7
2
θmax
10
8
4
2
φ (degrees)
Table 4.1: Measured epicardial fiber direction and anisotropy ratio for different methods:
direction of 1) fitted ellipse (Ellipse) and 2) maximum conduction velocity (θmax ). AR is
calculated based on: the ratio of 1) major and minor axis of fitted ellipse (Ellipse), 2)
longitudinal to transverse conduction velocities of fitted ellipse (θl /θt ), and 3) maximum to
minimum conduction velocity (θmax /θmin ).
estimated AR for the different methods considered. Table 4.1 shows that using the
θmax /θmin ratio results in the most accurate measurements (see Discussion Section
4.5). Similarly, Table 4.1 shows that measurement of fiber orientation based on θmax
yields a more accurate estimate than that based on the long axis of the best-fit ellipse to the isochrone. However, attempts to apply these alternative measures to
experimental data demonstrated that they are highly sensitive to experimental noise
and thus unsuitable for practical application. The remainder of the analysis in this
chapter is therefore based on fitting of ellipses to isochrones.
4.4.1.4 Effect of optical mapping
The measured membrane potential on the epicardium was calculated with the effect of
OM. Angle of propagation, anisotropy ratio, and conduction velocities were measured
70
and compared to the ones with no OM effect considered. Table 4.2 shows a complete
comparison between all the parameters with and without considering OM.
Table 4.2 shows that the OM caused more error (compared to the nominal AR
of 3) in AR measurement for thicker tissues, i.e., for the 1mm slab, AR is measured
as 1.63 and 1.72 with and without effect of OM respectively. These values are 2.76
and 2.94 for the 10mm slab (see Discussion section 4.5). This shows that OM is the
dominant cause of error in the thick tissues while the fiber rotation causes the major
part of error in the thin tissues.
The angle of wave propagation is also affected by the OM. The error is increased
from 24 degrees to 32 degrees for the thinnest tissue and from 2 degrees to 5 degrees
for the thickest tissue.
OM did not significantly change the measurements of θl (2-3% additional error)
for any tissue thickness. Transverse conduction velocities were affected more by the
OM (1-10% additional error) but the main cause of error was the fiber rotation. The
difference between simulations that did or did not account for OM was again more
pronounced in the thicker slabs. However, for all parameters considered, the errors
observed in thick tissues (due to either fiber rotation or OM) are relatively small and
unlikely to substantially affect experimental conclusions.
71
AR
φ wit(degrees)
θl (cm/s)
θt (cm/s)
OM
NOM
OM
NOM
OM
NOM
OM
NOM
1mm
1.63
1.72
32
24
46
46.7
45
45
2mm
2.13
2.23
22
16
46.8
47.4
30
27.3
4mm
2.58
2.72
10
7
47.5
48.6
22.6
19.8
1cm
2.76
2.94
5
2
48
48.9
19.3
17.7
Nominal
3
0
51
17
Table 4.2: Anisotropy ratio (AR), fiber orientation (φ), longitudinal and transverse conduction velocities (θl and θt ) with and without considering the effect of optical mapping
(shown in the table by OM and NOM respectively). It is evident that optical mapping
causes more error in measurements.
4.4.1.5 Effect of photon scattering
Equation 4.5 considers that the emission light travels in a linear path perpendicular
to the tissue to hit the surface. Hence, the calculated VOM is a weighted average
over the depth of the tissue. Another approach to model emission light is to consider
the effect of photon scattering. The emission light spread from the emission source
to reach the epicardial surface. Figure 4.8 shows the difference between these two
methods.
72
Figure 4.8: Different approaches to model emission light; exponential decay without (a)
and with (b) the effect of photon scattering.
The effect of photon scattering can be modelled by adding Γ(z 0 , ρ) to be the pointspread function, describing the flux Γ of photons emitted by the fluorescent dye at
point (x0 , y 0 , z 0 ) and exiting the tissue at point (x, y), with ρ the radial coordinate
p
on the imaged xy surface, centered around (x0 , y 0 ), i.e. ρ = (x − x0 )2 + (y − y 0 )2 .
The fluorescence optical signal VOM recorded from the surface point (x, y) can then
be obtained by
Z
VOM (x, y) =
Vm (r~0 ).Φe (r~0 ).Γ(z 0 , ρ).dr~0
(4.6)
V
One possible estimation of the spread function Γ is spherical photon scattering.
Therefore Γ(z 0 , ρ) can be written as:
p
z 02 + ρ2 Γ(z 0 , ρ) = exp −
,
δ
(4.7)
where δ = 1.34 mm is the attenuation constant of emission light in the cardiac tissue
[62, 39]. If the Eqn. 4.7 is used to calculate the measured membrane potential VOM
on the epicardium (z = 0), then Eqn. 4.7 can be re-written as:
p
−|r~0 | (x − x0 )2 + (y − y 0 )2 + (z − z 0 )2 Γ(r~0 ) = exp −
= exp
.
δ
δ
73
(4.8)
This equation is similar to Eqn.4.5 except that the variable z is substituted with |r~0 |
to model the scattering effects of emitted fluorescent light.
Measured VOM on the epicardium was calculated based on the above equations.
The results are shown in Fig.4.9 below. This figure clearly demonstrates that the
addition of photon scattering does not affect the results significantly. Isochrones are
completely parallel to each other and anisotropy and conduction velocity measurements are thus comparable.
Figure 4.9: Isochrones (5 ms intervals) based on the simulations of optical mapping without the scattering effect (“OM”, dashed lines) compared to isochrones obtained for the same
tissue using the photon diffusion approach (“OM+Scattering”, solid line). The times corresponding to each isochrone have been offset slightly between the two simulations to allow
a side-by-side comparison.
74
4.4.1.6 Effect of spatial discretization
To study the effect of space discretization, we have repeated three simulations with a
spatial discretization step of 50µm in all three directions (rather than the 100µm step
presented above). We chose a tissue thickness of 1 mm to ensure that we addressed
the worst-case scenario in which the effects of transmural fiber rotation are maximal.
Three scenarios were considered:
1) “Baseline” refers to the case without transmural fiber rotation and with transmural
(perpendicular to the epicardial surface) conductivity equal to transverse (parallel
to the epicardial surface) conductivity (gn = gt ).
2) “gn = gt ” refers to the case with transmural fiber rotation and with transmural
conductivity equal to transverse conductivity (gn = gt ).
3) “gn = 1/8 gt ” refers to the case with transmural fiber rotation and with transmural
conductivity reduced by a factor of 8 compared to transverse conductivity (gn =
1/8 gt ).
The results of these simulations are summarized below. Table 4.3 reports the
results for angle of propagation measurements. The anisotropy ratio is presented in
table 4.4. The effect of spatial discretization on longitudinal and transverse CV is
represented in tables 4.5 and 4.6 respectively.
Discretization
Baseline
gn = gt
gn = 1/8 gt
100µm
0◦
24.0◦
12.0◦
50µm
0◦
23.4◦
11.6◦
Table 4.3: Angle of propagation for different spatial discretization
75
Discretization
Baseline
gn = gt (cm/s)
gn = 1/8 gt (cm/s)
100µm
2.9
1.7 (59%)
2.2 (76%)
50µm
2.8
1.7 (61%)
2.1 (75%)
Table 4.4: Anisotropy ratio for different spatial discretization (percentages are percentage
difference from baseline)
Discretization
Baseline
gn = gt (cm/s)
gn = 1/8 gt (cm/s)
100µm
51.1
46.8 (91%)
48.2 (94%)
50µm
52.2
47.8 (91%)
49.8 (95%)
Table 4.5: Longitudinal conduction velocity for different spatial discretization (percentages
are percentage difference from baseline)
These results demonstrate that the values of these four measures are affected
by the spatial discretization step. This effect is more pronounced for transverse
conduction velocity under conditions of strong transmural uncoupling (gn = 1/8 gt ).
However, the results show that even under these extreme conditions, the difference
in transverse conduction velocity between the two spatial step sizes is 5% or less.
Numerical simulations always involve a trade-off between computational speed
and accuracy. Due to the 8-fold increase in the number of elements for the 50µm
simulations (compared to 100µm), the three simulations with 50µm discretization
presented here each required nearly 40 hours of computer time (sixteen core Intel
CPU 2.8 GHz, 32 GB RAM). This would increase even further for thicker tissues.
76
Discretization
Baseline
gn = gt (cm/s)
gn = 1/8 gt (cm/s)
100µm
17.4
45.5 (261%)
22.5 (139%)
50µm
18.3
46.1 (251%)
23.6 (129%)
Table 4.6: Transverse conduction velocity for different spatial discretization (percentages
are percentage difference from baseline)
4.4.2 Experimental Results
Figure 4.10 shows an activation map of a rat heart in the left panel. The right
panel shows the measurements of the angle of rotation of each isochrone versus time
elapsed after stimulation. The time scale starts 7ms after stimulus application to allow
accurate detection of activation and wave propagation. Since the exact epicardial fiber
direction is unknown, the angle difference is calculated by finding the angle of the
fitted ellipse relative to the angle of the 7ms isochrone. The rotation appeared to
continue at a similar rate, but isochrones reached to the boundary of the field of view
after 12ms and made it difficult to measure the angle of propagation reliably. The
angle of wave propagation changed with elapsed time, consistent with the simulation
results in Fig. 4.4. Experiments were performed on rat left ventricle with a thickness
of 3.5 ± 0.3mm. The change in angle difference between the 7ms and 10ms isochrones
was 6.8 ± 2.1 degrees. The change in angle was 6 and 2.3 degrees in simulation
results with the OM effect included for 2mm and 4mm tissues. The experiments were
designed to qualitatively observe the rotation of the isochrones.
The experimental results are closer to the simulation results for the 2mm tissue
rather than to the 4mm tissue. This can be caused by the significant measurement
error in how the thickness of the tissue was estimated. The cardiac tissue does not
77
have a uniform thickness in the left ventricle and endocardium has irregular formation
of trabeculae branches which signify the measurement errors. However, rather than
the tissue thickness, intramural conductivity (gn ) affects the angle of propagation as
shown in Figure 4.4. Therefore, even accurate measuring of the tissue thickness will
not provide precise information about the isochrone rotation since the changes in the
gn is equivalent to the changes in the tissue thickness and the exact value of gn in the
experiments is unknown.
(a)
(b)
Figure 4.10: (a) Activation map of a rat heart. The isochrones are described by black
lines. (b) Angle difference of wave propagation versus elapsed time after stimulus. The
angle of wave propagation has an increasing trend as the time passes after the stimulation
(n=6). Simulation results for 2mm and 4mm tissues are also provided. The angle of wave
propagation was determined based on the orientation of the long axis of the best-fit ellipse
to the activation time isochrones at the time indicated post stimulus.
Measurement of conduction velocities for experimental data based on the θmax
method, is sensitive to the noise. Figure 4.11(a) illustrates how noise in experimental
data can cause significant variability in measurements based on the direction of max78
imum conduction velocity. We cannot rule out that further refinement of this method
to smooth the results might improve this situation. However, it is worth noting that
the velocity estimates are based on a 7×7 pixel neighborhood (about 1.75×1.75 mm
with the magnification used for the experimental results shown here) and thus already
contain a significant element of smoothing. This method uses a moving average technique by moving a 7×7 window over the image and substituting the middle pixel by
the average of the window.
(a)
(b)
Figure 4.11: (a) Experimentally obtained activation isochrones from a rat left ventricular
free wall and the corresponding local velocity estimates (arrows, obtained based on a 7×7
pixel neighbourhood centered on the pixel of interest) in each pixel. (b) For easier visibility, the figure has been edited to show only three isochrones and the corresponding velocity
estimates along each isochrone. Note that velocity estimates near the apex of the isochrone
(highlighted) can vary significantly in direction between adjacent points. Using the direction
of the largest local velocity as an estimate of fiber orientation can thus lead to significant
variability from isochrone to isochrone.
79
4.5 Discussion
4.5.1 Effect of fiber rotation and wall thickness
It is clear that the cardiac tissue transmural fiber rotation has a significant effect on
the wave propagation patterns observed on the epicardium [61]. Thinner tissues have
fewer layers so there is a larger angle difference between layers. Electrical coupling
between nonaligned layers causes surface wave propagation not to follow fibre orientation. This misalignment is more significant in thinner tissues due to a larger angle
difference between the layers.
Figure 4.2 illustrates an ellipse fitted to the 20ms isochrone in the 1mm-thick
tissue (largest error). The fitted ellipse is not exactly directed to the direction of
wave propagation. The reason is in notches in the shape of isochrone which causes
the deviation between the direction of the isochrone and the ellipse. However, this
mismatch actually reduces the error, since the fitted ellipse is better aligned with the
epicardial fiber direction than the perceived “long axis” of the isochrone.
As the thickness of the tissue increases, adjacent layers have a smaller angle difference. Deeper layers are less electrically coupled to the epicardium and, thus, have
a smaller effect on surface wave propagation. This is demonstrated in Figure 4.3.
Figure 4.4 shows that the angle of propagation not only depends on thickness but
also varies with time after stimulation. It takes some time for activity to propagate
through the tissue to reach deeper layers. As the epicardial stimulus is delivered, the
electrotonic loading from deeper layers that have yet to activate initially limits the
epicardial conduction velocity. As deeper layers activate, the current contributed by
the deeper layers interacts with epicardial conduction and the wavefront observed on
the epicardium begins to rotate toward the fiber orientation of deeper layers. This
80
causes the epicardial wave front to change direction over time. The angle of propagation approaches steady state as the wavefront propagates through the whole tissue.
The experimental recordings confirmed that the isochrones rotate with time after the
stimulus application (Fig. 4.10). These recordings are qualitatively consistent with
the simulations as depicted in Fig. 4.4. The simulations appear to underestimate the
size of this response, i.e., the results of a simulation using a 2 mm thick tissue agree
quantitatively with experimental results obtained in 3.5 mm thick rat left ventricular
free wall. Possible reasons include the difference between the idealized model with
uniform epicardial fiber orientation and the real heart, which most likely exhibits
some change in epicardial fiber orientation over the field of view. It is also possible
that the thickness measurement over-estimated the left ventricular wall thickness, as
these measurements were obtained by slicing the heart open after the experiment,
which may have allowed the heart to contract somewhat compared to its state during
perfusion.
4.5.2 Effect of transmural conductivity
Another parameter that affects electrotonic loading is the amount of electrical coupling between the layers, which is described by transmural conductivity (gn ). Lower
transmural conductivity results in a weaker coupling between the layers and therefore,
less electrotonic effect from the layers beneath the epicardium. As depicted in Fig.
4.4 and Fig. 4.5, in all thicknesses, tissues with lower transmural conductivity have
smaller angle of deviation from the epicardial fiber direction. However, even in the
extreme case of gn = 81 gt , thinner tissues still show substantial deviation. The effect
of transmural conductivity is more pronounced with time. As time passes and other
layers become excited, underlying layers have more electrotonic loading effect on the
81
epicardium so the effect of transmural conductivity is more visible. Reducing transmural conductivity is mathematically equivalent to increasing tissue thickness. It is
therefore not surprising that the effects of changing transmural conductivity parallel
the effects of changing tissue thickness.
4.5.3 Effect of optical mapping
Table 4.2 shows a complete comparison between all the parameters with and without
considering the effect of OM. It can be seen from Table 4.2 that when taking OM
effects into account, measurement errors in structural parameters of cardiac tissue
(AR, angle of propagation, θl , and θt ) are exacerbated due to light decay effects.
Therefore, in general, OM effects increase error in measurements.
It can be also noted from Table 4.2 that for thicker tissues, the dominant cause
of error is OM and in thinner tissue, the dominant cause of error is electrotonic
loading from underlying layers. In 1mm thick tissue, OM has a negligible effect
on the measurements and the measurement error arises primarily from electrotonic
effects due to fiber rotation. In a 1cm slab, fiber rotation causes small error when
OM is not considered. Accounting for OM increased measurement error significantly.
This is due to the fact that in thin tissues, electrotonic loading effects are stronger
and, also, photons decay less and recorded light intensity is affected more by the light
intensity of underlying layers.
4.5.4 Implication for experimental measurements
Distortion of wave propagation causes errors in estimates of epicardial fiber direction,
as well as in measurements of conduction velocities and anisotropy ratio [61]. Our
simulations and experimental observations show that the error in the estimated fiber
82
orientation increases as time elapses post-stimulus. Measurements should therefore
be done as soon as possible after stimulation to ensure that electrotonic effects are
minimized. Simulation results confirmed that this observation applies not only to
the estimated fiber orientation, but to measurements of AR as well (whether based
on the ratio of long to short axis of the fitted ellipse or based on conduction velocities). However, it is important to recognize that measurements obtained during, or
immediately after, the stimulus pulse mainly reflect passive depolarization due to the
injected stimulus rather than true propagation of the action potential. Also, during
the early stages of propagation, there is a significant component of transmural propagation (perpendicular to the plane of imaging) as deeper layers are activated. For
both these reasons, sufficient time must be allowed between the stimulus pulse and
measurement of fiber orientation, conduction velocities, and AR.
The nominal AR value of the tissue in Fig. 4.6 is equal to 3, calculated in a
tissue with no fiber rotation. Fitting ellipses to the activation time isochrones and
considering the direction of propagation equal to the direction of those ellipses, not
only yields an inaccurate estimate of the fiber orientation (Fig. 4.3, 4.4, and 4.5) but
also results in an error of the AR (Fig. 4.6). As previously explained, when transmural
conductivity decreases, epicardial wave propagation is less distorted. Therefore, AR
measurements are more accurate for tissues with smaller transmural conductivity,
especially for thicker tissues. Measurements in thinner tissues are more accurate
when transmural conductivity decreases but there is still significant error (even in the
extreme case of gn = 81 gt ) due to high electrical coupling. Errors in 1cm thick tissue
are not large enough to be considered physiologically relevant and are presented in
this chapter for the sake of comparison and to support the observation that fiber
rotation has more effect in thinner tissues. However, errors in thinner tissues are
83
relevant to experiments in rat or mouse ventricles.
Measurement of conduction velocities is also affected by the tissue fiber rotation.
As the fitted ellipse is not aligned with fiber orientation on the epicardium, measured
velocities are not in the longitudinal and transverse directions either so the measured
θl has a component of transverse conduction and is smaller than the true θl . The
measured θt has a component of longitudinal conduction and is larger than the nominal θt . The measured θt in thinner tissues with higher gn has significant error that
can be attributed to the notch in the isochrones of activation maps for these tissues.
This notch is clearly shown in Fig. 4.3, in 1 and 2mm-thick tissues, and has been
observed in previous studies [52, 53]. The larger the notch is, the less accurate are
the measured transverse conduction velocities.
In an attempt to reduce the errors incurred in estimating fiber orientation and
AR experimentally, we investigated alternative measurement approaches based on
conduction velocity measurements rather than isochrones. In particular, estimates
based on maximum and minimum conduction velocities along an isochrone (20 ms
in this study), appeared to yield significantly improved estimates of fiber orientation
(based on the direction of θmax ) and AR (based on the ratio θmax /θmin ) when applied
to simulated (noise free) data. However, in practice, these measures proved to be too
sensitive to experimental noise and low pixel resolution to be of practical use. Among
the methods considered in this work, our recommendation is thus that experimental
measurements of fiber orientation and AR should be based on the best-fit ellipse to a
suitable activation isochrone. The measurement errors identified should be taken into
account when interpreting these observations. We cannot rule out that alternative
methods, providing a smoother estimate of conduction velocities, may yield a better
estimate of fiber orientation and/or AR. However, it is worth noting that our estimate
84
of conduction velocities, being based on a 7 × 7 pixel (approximately 1.75 × 1.75mm)
area, already employ significant smoothing.
Our results also showed that reduced coupling between the layers (in the direction normal to the epicardial surface) results in more accurate measurements. One
may therefore be tempted to use an uncoupler (e.g. Heptanol) during experiments.
However, application of a gap junction uncoupler will clearly affect coupling in all
directions. In addition, the effect of an uncoupler may be somewhat different in different directions since the conductivity along the fibers is due to both myoplasm and
gap junction conductivity, while across the fibers, the conductivity is mainly due to
the gap junctions. Thus, using an uncoupler is not likely to improve estimates of AR,
θl , θt , and fiber orientation in a predictable manner.
It is also worth noting that using near-infrared dyes as described by Walton et
al. [63] will cause increased optical contributions from the underlying layers in the
recordings and, therefore, will result in less accurate measurements in this context.
These dyes do have useful applications due to their ability to penetrate deeper into the
tissue. However, for the measurements discussed in this chapter, a shorter penetration
depth (shorter-wavelength dyes) is preferable.
4.5.5 Study limitations
The experimental optical mapping data has limited spatial and temporal resolution
due to the characteristics of the optical system which are not considered in the simulations. Derived images also have motion artifacts that can cause inaccuracy in the
data processing step, in particular for the repolarization phase. Since our calculation and measurements are based solely on the activation times, the impact of these
motion artifacts on our results expected to be minimal.
85
The 100µm spatial step size used in this work is a trade-off between computational
speed and accuracy as in any numerical simulation. To assess the sensitivity of the
results presented in this chapter to the spatial step size, we repeated three simulations
with a refined step size of 50µm. We chose a tissue thickness of 1mm and repeated the
simulations for a) no fiber rotation and gn = gt , b) with fiber rotation and gn = gt , and
c) with fiber rotation and gn = 18 gt . This ensured that the “worst-case” scenario, with
the most pronounced transmural voltage gradients (case c), was included. Values for
angle of propagation, anisotropy ratio, and conduction velocities remained within 5%
of the values obtained with 100µm step size, confirming that the conclusions of this
chapter do not depend on the exact spatial discretization. As expected, the largest
differences were observed for transverse conduction velocity in case c).
Our model of tissue does not include all the structural details such as curvature,
cleavage planes, and Purkinje system. The tissue slabs used in our simulations are
rectangular parallelepipeds which have no curvature. Cleavage planes, which are
located between muscle layers, are not included in the model. Purkinje fibers, which
are located in ventricular walls and conduct action potential more quickly, are not
included in our model. These limitations can be addressed by considering a model
with more detail but this would result in higher computational cost.
4.6 Conclusion
This chapter showed that fiber rotation causes error in conventional measurement
methods used to estimate fiber orientation and anisotropy ratio. These errors are
affected by the tissue thickness and intramural conductivity and are increased by
optical effects during optical mapping recordings. Despite significant errors in thin
86
tissue preparations, the most appropriate method (at least of the ones considered here)
for estimating fiber orientation and AR experimentally appears to be least-squares
fitting of an ellipse to an activation time isochrone.
87
Chapter 5
Diabetes and Vulnerability to Arrhythmias
The majority of the contents of the following chapter has been prepared to be
c
submitted in PLOSone
5.1 Chapter Specific Background
In recent years many studies have been performed of the electrophysiological differences between healthy and diabetic cardiac myocytes [64, 65, 66] and the vulnerability
of diabetic hearts to cardiovascular disease such as arrhythmias [67, 68].
In the setting of type I diabetes, the heart is often considered to be at higher risk of
developing arrhythmias or other cardiovascular diseases such as myocardial ischemia
[69]. Myocardial ischemia results in changes in biochemical and electrophysiological
characteristics of the heart that can lead to an unstable electrical substrate which
can be able to initiate and sustain arrhythmias. Ischemia can also cause infarction
leading to unexcitable tissue and conduction block, which increases the chances of
reentrant activities in the heart that is arrhythmogenic.
Many studies have shown that diabetic hearts are more susceptible to ischemic
injuries compared to healthy models [70, 71, 72, 73]. However, some studies indicated
no difference [74, 75, 76], or even less sensitivity [77, 78, 79, 80, 81, 82] of diabetic
hearts to ischemia in comparison to healthy hearts. Cardiac ischemia results in the
opening of ATP dependent potassium channels (KATP) which is due to the lack
of ATP in the heart [83]. Activation of the KATP current results in a significant
88
decrease in action potential duration (APD) [84]. Shortening of the action potential
could introduce an additional risk of developing arrhythmias due to shortening of the
refractory period.
Some studies directly discussed the effect of diabetes on susceptibility to arrhythmias. However, contradictory results were presented by different groups. For example
on one hand, Ravingerova et al. [79] compared the susceptibility to ventricular arrhythmias in rats with prolonged duration of STZ-induced diabetes using both open
chest rats in vivo and isolated Langendorff-perfused hearts. Following 8 weeks of
STZ-induced diabetes, they subjected both models to 30 minute regional zero flow
ischemia induced by occlusion of the left anterior descending (LAD) coronary artery.
Their observations suggested that rat hearts with chronic diabetes are less sensitive
to ischemic injuries and less vulnerable to ventricular arrhythmias in both models.
On the other hand Zhang et al. [67] performed whole cell patch-clamp studies in
a rabbit model of alloxan-induced diabetes mellitus. They demonstrated changes in
ionic currents and observed a 20% prolongation of action potential duration. They
also showed that the QT prolongation in a diabetic rabbit model resulted in occurrence of arrhythmias, mainly of ventricular tachycardia (VT) lasting longer than
30s, which was otherwise absent in their control model. These observed VT lead to
ventricular fibrillation (VF) causing sudden death.
In this chapter, the effects of diabetes on reentrant arrhythmias are studied using
computer modelling. Reentry is a circular or spiral propagation of an action potential
which is happening due to different refractory period and conductivities of different
pathways. Reentry is a common cause of arrhythmias such as ventricular tachycardia
[85] and atrioventricular node reentry [86]. It can occur when a conduction path is
partly slowed down or completely blocked in one direction (uni-directional block) due
89
to reduced electrical conductivity.
Conductivity of a tissue is dependent on intercellular protein channels called connexins located on gap junctions. A major component of cardiac gap junctions is
connexin 43 (Cx43) which is known to migrate from cell ends to cell sides in diabetic
hearts (known as connexin lateralization) [21]. This change from regular arrangement
of gap junctions affects propagation, increasing risk of arrhythmias [87, 88]. The gap
junctions can be affected by a variety of factors, including pharmaceuticals [89] and
diseases [90]. Seidel et al [91] simulated the connexin lateralization in a rat ventricle computer model and showed that the susceptibility to conduction block at tissue
expansion becomes significantly higher as a negative effect of connexin lateralization.
Diabetes also affects the calcium handling inside the cardiac cell [92, 93]. Changes
in the sarcoplasmic reticulum (SR) calcium load ([Ca2+ ]SR ), decreased rates of calcium
depletion from and uptake to the SR, and the depressed efflux of calcium through
Na+ /Ca2+ exchanger current (NCX) can alter the intracellular calcium concentration
([Ca2+ ]i ). However, these abnormalities cause opposite effects on [Ca2+ ]i . Decreased
[Ca2+ ]SR and reduced depletion of Ca2+ from SR reduce [Ca2+ ]i while reduced uptake
of Ca2+ to SR and regulation of NCX results in higher [Ca2+ ]i . High levels of
[Ca2+ ]i can result in spontaneous calcium release current into the sarcoplasm through
“calcium induced calcium release” (CICR) mechanism. This can increase depolarizing
NCX current which itself is arrhythmogenic and can lead to early (EAD) or delayed
after depolarization (DAD).
Rabbit ventricular action potentials are significantly longer than those of rat ventricular myocytes. Unlike rabbit myocytes, rat ventricular myocytes lack a welldefined plateau phase during repolarization. This is due to relatively large outward
repolarization currents in rat that bring the membrane potential rapidly close to rest90
ing potential [94]. The plateau phase in rabbit AP is due to the balance between
inward ICaL and outward delayed rectifier potassium current.
In this chapter, we simulated the vulnerability to reentrant arrhythmias in healthy
and diabetic myocardium for rat and rabbit models. Connexin lateralization was
implemented in diabetic tissue and the effect of IKATP opening in ischemic conditions
was also discussed for both control and diabetic models.
5.2 Methods
5.2.1 Rat Model
The Pandit mathematical models of rat ventricular myocytes were used for healthy
[51] and diabetic [95] single cell models. A summary of the differences between these
models is provided in Fig. 5.3. Single cell action potentials were simulated in MATLAB. A 1cm×1cm two dimensional tissue was created using CARP (cardiac arrhythmia research package [32]).
5.2.2 Rabbit Model
In this chapter we used a rabbit ventricular action potential mathematical model of
cardiac single cell from Mahajan et al. [96] as a baseline control model. Changes from
Zhang et al [67] were applied to this model and single cell simulations were performed
with MATLAB.
5.2.2.1 Summary of the rabbit mathematical model
Figure 5.1 shows a schematic diagram of the rabbit model from Mahajan et al [96].
Sodium current (INa ) and L-type calcium current (ICaL ) are the only inward ionic
channels. ICaL is modelled by a seven-state Markovian mechanism. Outward potas91
sium currents consist of fast and slow transient outward currents (Ito,f and Ito,s respectively), slow and rapid delayed rectifiers (IKs and IKr respectively) and inward
rectifier current (IK1 ). The sodium-potassium pump is also included in the model.
A basic calcium cycling mechanism is included in the model. Ca2+ enters the cell
in the dyadic junction through ICaL . The dyadic junction is a subset of submembrane
space. Sodium-calcium exchanger (Na+ /Ca2+ ) and INa are connected to the submembrane space. Ca2+ depletes from the junctional sarcoplasmic reticulum (JSR) to
the dyadic junction by Jrel . Ca2+ is uptaken to the network sarcoplasmic reticulum
(NSR) by Jup . Some Ca2+ ions leak from NSR to cytoplasm, which is modelled by
Jleak .
Figure 5.1: Schematic diagram of the rabbit model from Mahajan et al [96], featuring
whole-cell model showing basic elements of Ca cycling machinery and membrane ion currents, as well as a seven-state Markovian model of the L-type Ca channel. Adapted under
a Creative Commons Attribution 3.0 Unported license; Online: https://goo.gl/3UFyYH;
License: http://goo.gl/TGFja
92
5.2.2.2 Changes in diabetic rabbit
Zhang et al [67] performed whole cell patch-clamp studies in a rabbit model of alloxaninduced diabetes. They observed a 20% increase in the action potential duration
(APD) of diabetic heart and changes in several ionic currents in diabetic rabbit single cell. Transient outward potassium current (Ito ) reduced by 60%, rapid and slow
delayed rectifier K+ currents reduced 70% and 40% (IKr and IKs ) respectively. However, they did not observe any changes in time-dependent kinetics of these currents.
L-type calcium current (ICaL ) peak amplitude was decreased by 22% and inactivation kinetics were slowed resulting in a total reduction of 15% in ICaL . Other ionic
currents and kinetics did not change such as the inward rectifier K+ current (IK1 ) and
sodium current (INa ). Calcium handling abnormalities such as those affecting sodium
calcium exchanger current (NCX), the uptake current (Jup ) via SERCA pumps in the
sarcoplasmic reticulum (SR) and the release of Ca2+ from SR were also included in
the model as discussed in [93]. A summary of these changes are provided in Fig 5.4.
5.2.3 ATP-dependent potassium channels (IKATP )
The ATP-dependent potassium channels are inactive in healthy cells, but an outward
current through them increases as the ATP levels decrease [83]. The formulation for
this current was acquired from Shaw and Rudy [84], and the current was added to
the single cell model implementation. The amplitude of ATP-dependent potassium
channel (IKATP ) was controlled by the conductance value, gKATP . Single cell simulations were performed in MATLAB to study the effect of IKATP opening on healthy
and diabetic single cell action potential. IKATP conductance (gKATP ) was set to zero
when it was considered to be close. gKATP was considered 1nS and 2nS in healthy
and diabetic rat single cell models to consider two different amplitudes of IKATP . The
93
maximum value of gKATP that resulted in generation of an AP in single cell was 2.4nS
and 2.6nS for the healthy and diabetic rat models respectively. These values were
7.2nS and 7.9 for the healthy and diabetic rabbit models. Three different values of
gKATP (3, 4 and 5nS) were used in rabbit simulations to account for the effects of
IKATP on the vulnerability to reentrant arrhythmias.
5.2.4 Spontaneous Calcium Release
Spontaneous calcium release (Jspon ) in a single cell was modelled by a calcium release
from the sarcoplasmic reticulum (SR) to the cytoplasm using the approach introduced
by Xie et al. [97]:
Jspon = Gspon × g1 × g2 × (
vs
cj − cs )
vSR
1
1 + exp(−(t − t0 )/τ1 )
1
,
g2 =
1 + exp((t − t0 )/τ2 )
g1 =
(5.1)
(5.2)
(5.3)
where Gspon is the maximum conductance with the value of 0.0674 mS−1 , τ1 = 10ms
and τ2 = 30ms, vs and vSR are volumes of submembrane space and SR respectively.
cj and cs are the calcium concentration in the junctional and SR respectively. The
release time is controlled by t0 in the equation.
5.2.5 Connexin Lateralization
In the healthy tissue the longitudinal conductivity (gl = 0.174 S/m) is almost 9
times greater than transverse conductivity (gt = 0.019 S/m, and gl /gt ≈ 9) [98].
Connexin lateralization in diabetic tissue was modelled by reducing the longitudinal
conductivity as connexins travel from cell ends to cell sides. Lateralized connexins
94
were considered not to be functional, therefore gt was not changed and gl was reduced
so that gl /gt ≈ 5.
We performed simulations considering functional lateralized connexins in diabetic
rat tissue. Results showed that the vulnerability was significantly reduced in these
models (window of vulnerability was 1ms and 5ms for diabetic rat with and without
IKATP respectively) not comparable to modeling and clinical literature [21] therefore
we didnt pursue the assumption of functional lateralized connexins.
5.2.6 Tissue Simulations
Using ionic models for healthy and diabetic rat ventricular myocytes from Pandit et
al. [51, 95] and healthy and diabetic rabbit ventricular myocytes explained previously
in 5.2.2, simulations were performed to study the effect of diabetes on arrhythmia vulnerability. Single cell models of healthy and diabetic rat and rabbit cardiac myocytes
were used to create a 1cm×1cm and 2cm×2cm two dimensional tissue for rat and
rabbit respectively using CARP [32]. The time step was 1µs and spatial discretization
of 100µm was used to solve mono-domain equations in the aforementioned 2D tissue
(1cm×1cm tissue for rat and 2cm×2cm for rabbit simulations). The larger physical
dimensions of the rabbit 2D model accounts for the difference in size and action potential duration (APD) between rat and rabbit hearts. There was no reentry in a
1cm×1cm tissue for rabbit (see Section 5.4.2).
5.2.7 Reentrant Arrhythmias
An S1-S2 stimulation protocol was applied to generate reentrant activity. As depicted
in Fig. 5.2, S1 occurred at the top edge of the tissue and propagated down (transversely) through the tissue. S2 occurred a certain time later in the top right corner
95
of the tissue. S2 occupied
1
4
of the tissue in area. Reentry was considered successful
if the wave traveled around at least twice to its starting point following generation of
S2. In this case the delay between S1 and S2 was noted. The range of S1-S2 delays
that resulted in successful reentry was called the window of vulnerability (WoV). The
larger the WoV, the more vulnerable the tissue is to reentrant arrhythmias.
Figure 5.2: S1-S2 stimulation protocol (left to right) - In (a) delay is too short and second
stimulus cannot propagate at all. Reentrant activity happened in (b) and stimulus rotates
through the tissue permanently. If the delay is too large then the stimulus propagates through
the tissue and vanishes (c).
5.2.8 Conduction Reserve
Conduction velocity is mainly dependent on two major parameters in the heart: excitability and coupling. There is a significant redundancy in these parameters which
96
is known as conduction reserve. Conduction reserve means that a small reduction
in conduction velocity requires significant reduction in excitability or coupling; or
moderate reduction in both factors [99].
Conduction velocity was measured for rabbit and rat model on a 5mm simulated
cable composed of 50 cells. Each cell is 100µm long. Activation time is the time when
a cell is excited and was considered to be the time when membrane potential crossed
0V . This was implemented by a linear interpolation between the discrete time points.
Conduction velocity was measured from the 10th cell to 40th in the model in order to
avoid the effect of sealed boundary conditions.
5.3 Results
5.3.1 Single cell APD is increased by diabetes
Figure 5.3 shows the single cell simulation of action potential in the healthy and
diabetic rat model. The diabetic action potential is longer mainly due to reduced
potassium currents as explained by [95]. Changes in diabetic ionic currents and
calcium handling characteristics are presented in the table of Fig. 5.3.
Figure 5.4 shows the simulation results of action potentials of normal and diabetic
rabbit model. APD was increased by 20% in diabetic rabbit model simulation results consistent with observations in [67]. The changes in diabetic ionic currents are
provided in the table of Fig. 5.4.
5.3.2 IKATP shortens APD more in diabetic tissue than in healthy tissue
Opening of IKATP results in more outward potassium current and shorter action potential consequently as depicted in Figures 5.5 and 5.6. However, the effect of IKATP
97
Currents
diabetic rat
It
-32%
Iss
-23%
ICaL
-24%
IBCa
-50%
IBNa
+25%
NCX
-40%
INaK
-37%
Jup
-20%
Jrel
-45%
Figure 5.3: Changes in diabetic rat ionic currents based on [95] and simulation results
of normal and diabetic action potential in a rat single cell. Action potential duration is
increased in diabetic rat.
98
Currents
diabetic rat
Ito
-60%
IKr
-70%
IKs
-40%
ICaL
-15%
IK1
NA
INa
NA
NCX
-40%
Jup
-20%
Jrel
-30%
Figure 5.4: Changes in diabetic rabbit ionic currents based on [67, 93] and simulation
results of normal and diabetic action potential in a single cell. Action potential duration is
increased by ∼20% in diabetic model.
99
(a)
(b)
Figure 5.5: Effect of IKATP opening on action potential in (a) healthy and (b) diabetic
single cell rat model- Opening of ATP potassium channels reduces the diabetic action potential duration by ∼29% but the same amount of IKATP results in ∼20% reduction of healthy
APD.
is not identical in healthy and diabetic cells. In rat, opening of IKATP , when gKATP
is 1nS, results in ∼29% and ∼20% APD reduction for diabetic and healthy models
respectively. In the rabbit model, diabetic APD was decreased by ∼15% by opening
of IKATP whereas this resulted in ∼8% APD shortening for the healthy model.
5.3.3 Connexin lateralization does not affect source-sink relationship for an ectopic
beat
We simulated a 2D sheet with only the cells at the top right corner region exhibiting
spontaneous calcium release in the rabbit model. The size of this region was changed
to find the minimum size of the tissue for which spontaneous release resulted in wave
propagation in the whole tissue (Fig. 5.7). The results showed that despite connexin
lateralization and current changes in diabetic tissue, the minimum size was similar for
100
(a)
(b)
Figure 5.6: Effect of IKATP opening on action potential in (a) healthy and (b) diabetic
single cell rabbit model- Opening of ATP potassium channels reduces the diabetic action
potential duration by ∼15% but the same amount of IKATP results in ∼8% reduction of
healthy APD.
101
both healthy and diabetic tissue. The moderate uncoupling resulting from connexin
lateralization thus does not appreciably affect source-sink relationship for an ectopic
beat.
Figure 5.7: A 2×2 cm tissue was used in simulations. The top right corner square regions
are used to find the minimum size of the tissue with spontaneous Ca release which results
in wave propagation in the whole tissue. The minimum square was 0.3×0.3 cm for both
healthy and diabetic rabbit model.
5.3.4 Vulnerability to reentry
Simulations were performed with and without IKATP and for different levels of coupling. For the rat model gKATP was either 1nS or 2nS while gKATP was considered 3,
4, and 5nS for rabbit. Gap junction conductivities were considered to be at 100%,
75%, 50%, and 25% of their baseline values.
Simulation results are shown in Fig 5.8 and 5.9. In the rat model (Fig. 5.8), WoV
was larger in the healthy tissue than the diabetic tissue in all cases. WoV increased
102
as the coupling was decreased in healthy and diabetic models. Opening of IKATP
resulted in larger WoV.
In the rabbit model (Fig. 5.9), the WoV is significantly larger in the diabetic
tissue than the healthy tissue which is the complete opposite of the results for the
rat model. Reduced coupling and increased IKATP resulted in a larger WoV, which is
similar to the rat model.
In Fig. 5.9, when there is no IKATP , no reentrant activity was observed in rabbit
models. Similarly when gap junction conductivities were not changed, there was no
reentrant arrhythmia in any healthy and diabetic rabbit models. As gap junction
conductivities are decreased and IKATP current increases, reentry was observed in
rabbit models. The WoV was larger in diabetic rabbit than in healthy one.
5.3.5 Rabbit and rat have the same conduction reserve
Figure 5.10 shows the conduction velocity versus coupling for rat and rabbit models.
The relationship between CV and coupling saturates as coupling increases and becomes steeper as cells are uncoupled. This robustness of CV against reduced coupling
is called the conduction reserve. In healthy models, coupling is in the saturated region
and moderate uncoupling does not affect CV significantly. With increased degrees
of uncoupling (such as connexin lateralization in diabetes), a small reduction in coupling results in a significant decrease in CV. Figure 5.10 shows that the rabbit and
rat models have similar conduction reserve plots and a particular change in coupling
thus results in the same change in CV in both species .
These simulations were done for healthy models of rat and rabbit. Results for
the diabetic models are identical to the results of the healthy models. Conduction
reserve is mainly dependent on the coupling and excitability. Coupling depends on the
103
(a)
(b)
Figure 5.8: Window of vulnerability for healthy (a) and diabetic (b) rat models. As the
conductivity is reduced in both models, WoV increases. Adding IKATP increases the WoV
in both cases.
104
(a)
(b)
Figure 5.9: Window of vulnerability for healthy (a) and diabetic (b) rabbit models. As the
conductivity is reduced in both models, WoV increases. Adding IKATP increases the WoV
in both cases. There was no reentrant activity observed when coupling was 100% or when
there was no IKATP in neither healthy nor diabetic rabbit models. Also when coupling was
set to be 75%, no reentry observed when gKATP was 3nS or 4nS for neither of healthy nor
diabetic rabbit.
105
Figure 5.10: Relationship between conduction velocity and conductivity for rat and rabbit
models. There is no significant difference between the two models.
sodium current (INa ) and extracellular potassium concentration ([K+ ]e ). As shown
in Fig.5.3 and Fig.5.4, none of these two parameters changed in diabetic rat and
rabbit respectively. Therefore, there is no difference between diabetic and healthy
conduction reserve plots (CV vs coupling). Ghaly et al. showed that 50% block
of Cx43 conductivity resulted in 17% CV slowing in healthy hearts while the same
amount of uncoupling resulted in 26% of CV slowing in diabetic heart [99].
5.3.6 Rabbit and rat have different APD restitution
Figure 5.11 shows the APD versus diastolic interval (DI) for rat and rabbit models.
The S1S2 protocol was implemented by stimulating each model 20 times with basic
cycle length (BCL) equal to one second (pre-pacing). S2 applies with varying time
delay after S1 and APD of the S2 stimulus was measured.
Restitution curve for the rabbit model has a positive slope for both healthy and
106
(a)
(b)
Figure 5.11: S1S2 APD restitution curves in single epicardial ventricular cell simulations
using (a) rat[51] and (b) rabbit [96] electrophysiological models of cardiac action potential
107
diabetic cells which means APD decreases as the stimulation frequency increases.
Surprisingly, the restitution of the rat model has a negative gradient as depicted in
Figure 5.11(a) in healthy and diabetic models. This represents APD prolongation as
BCL decreases (stimulation frequency increases).
Diabetes did not change the overall shape of restitution curves in each model.
APD was increased in diabetic models as explained before.
5.4 Discussion
5.4.1 Diabetes decreases arrhythmia vulnerability in rat
The simulation results presented in Fig. 5.8 show the window of vulnerability for
healthy and diabetic rat model. Figure 5.8(a) shows that in healthy rat model when
the coupling is reduced the WoV is prolonged regardless of opening of the ATP
potassium channels. Also for a specific coupling level, WoV increased as IKATP opened.
Opening of IKATP channels results in shortening of action potential duration that also
increases the vulnerability to reentrant arrhythmias. These effects are similar for
diabetic rat as depicted in Fig. 5.8(b). It is worth noting that the reentry occurs
earlier in the presence of IKATP for a specific amount of coupling (bottom of WoV
range is lowered as IKATP increased). Shortening of APD due to opening of IKATP
results in shorter refractory period and therefore reentry occurs earlier as APD is
reduced. On the other hand, as coupling was reduced for a specific amount of IKATP ,
reentry occurred later and the bottom of WoV shifted up. Reduced coupling results in
reduced conduction velocity and causes the wavefront to propagate slower requiring
a later S2 stimulus to initiate reentry.
The WoV depends on the duration of relative refractory period, and once reentry
108
is initiated, its survival depends on the electrical pathlength of the tissue. Opening of
IKATP channels results in a shorter APD and hence, shorter refractory period. On the
other hand, shorter APD results in shorter wavelength and therefore longer available
electrical path. Electrical available pathlength is inversely proportional to the wavelength and therefore IKATP opening results in longer available electrical pathlength for
sustaining reentry activity. Both of these effects (shorter APD and shorter λ) favor
longer WoV, which explains why the WoV charts are larger when IKATP channels open
in Fig. 5.8(b).
Comparing healthy and diabetic rat results shows that the onset of arrhythmia is
earlier in the healthy model. This may be unexpected at first glance as the coupling
is reduced in diabetic tissue and conduction slowed. However, one may note that the
APD is considerably longer in diabetic tissue, and that this effect dominates over the
reduced conduction velocity. Figure 5.8 shows that for a specific amount of coupling
and IKATP , WoV is longer for healthy rats showing that the healthy model is more
susceptible to reentrant arrhythmias. Our results for rat model are in agreement
with experimental results obtained by [77, 79, 80, 81]. This contradicts experimental
results that showed the likelihood of arrhythmia in STZ-induced diabetic hearts are
more than that in control hearts [70, 71, 72, 73].
5.4.2 Diabetes increases arrhythmia vulnerability in rabbit
Figure 5.9 represents the simulation results of S1-S2 protocol on healthy and diabetic
rabbit model. Our diabetic rabbit model was developed using the mathematical
model of healthy rabbit developed by Mahajan et al [96] incorporating the diabetic
alterations reported by Zhang et al. [67]. It has to be noted that there was no
reentrant activity in healthy or diabetic rabbit model when the gap junction coupling
109
was not altered and when there was no IKATP . Figure 5.9 shows that when coupling
is 75% of the base healthy or diabetic model, reentry occurred when gKATP was equal
to 5nS and no reentry observed for smaller gKATP . The effect of IKATP opening in
the rabbit model is similar to the effect of IKATP opening in the rat model and can
be explained as discussed before.
As IKATP increased (by increasing gKATP ), WoV was prolonged for specific amount
of coupling and the reentry happened earlier. Comparing Fig. 5.9(a) and 5.9(b)
it is evident that, for every corresponding case, WoV is significantly larger in the
diabetic model. The minimum S1-S2 interval that resulted in reentry increased for
the diabetic model since the APD is longer. This is in agreement with experimental
results obtained in rabbit [70, 72] and rat models [73, 100]. This difference is more
significant as coupling decreased, suggesting that the diabetic model vulnerability is
more sensitive to uncoupling than the healthy model. The cardiac conduction velocity
is nonlinearly related to gap junction conductivity and substantial changes in gap
junction conductivity results in small changes in conduction velocity. This is known
as “conduction reserve”. Reduced coupling in the diabetic rabbit model resulted
in considerably more increment in WoV comparing to the increment of WoV in the
healthy diabetic model. Conduction reserve is known to be reduced in diabetic hearts
as previously shown by Nygren et al. [21] mainly due to the connexin lateralization.
The required physical pathlength for a sustaining reentrant arrhythmia is determined by the concept of “wavelength” being equal to conduction velocity multiplied
by APD introduced by Smeets et al [13]. Simulation results indicated that there was
no reentry in 1cm×1cm rabbit tissue, which is reasonable since the APD is significantly longer in rabbit than in rat and therefore the reentrant wavelength is larger in
rabbit requiring larger tissue for propagation. The rationale for the fact that we used
110
a larger size of the tissue for rabbit than in rat in this study can be explained in terms
of different physical heart sizes of the species. Assuming that the hearts shapes and
anisotropy ratios of two hearts are similar, one way to find the relative sizes of the
hearts is to find the cubic root of relative volumes or masses [101]. The average heart
weight of a medium rat is reported as 0.991g [102] and the average heart weight of a
rabbit is 10.2 g [103] resulting in the relative heart size of 2.17. Thus, our assumption
that the linear dimensions of the rabbit heart are twice those of the rat heart roughly
approximates the difference in physical heart size between the two species.
5.4.3 Diabetes did not change the source-sink relationship
Figure 5.7 showed no difference in the size of the tissue having spontaneous calcium
release that propagated through the whole tissue. Xie et al. [97] showed that the number of the myocytes required to elicit an EAD or DAD to trigger a propagating action
potential was dramatically changed as the gap junction conductivity was decreased.
However, they reduced the gap junction conductivity six-fold in all directions while
in our simulations the conductivity was reduced only in longitudinal direction and
by less than a 2 fold. Also the S2 stimulus in our simulations was applied at the top
corner of the tissue as shown in Fig. 5.7, while Xie et al. [97] applied the spontaneous
release at the center of the tissue. Because of the symmetry, the release of calcium
in the top corner in our simulations is electrically equivalent to release from a four
times larger region, centered in a four times larger tissue. Therefore, our simulation
result is equaivalent to a central square release in a 6mm×6mm region in a 4cm×4cm
tissue. However, Xie et al. showed that the major axis of the elliptic region that
elicits the EAD decreased from 14.1mm to 5.7mm when gap junction conductivity
was reduced six-fold in all directions. This suggests that the source-sink relationship
111
was mainly affected by the significant reduction in conductivity. Diabetes and AP
prolongation did not affect the source-sink relationship significantly at the resolution
of our simulations.
5.4.4 Diabetes has different effects on arrhythmia vulnerability in different species
WoV can be considered in terms of electrically equivalent tissue sizes, i.e. when x/λ is
constant, where x is the physical length of the tissue and λ is the wavelength. Figure
5.10 shows that the CV is similar for rat and rabbit models. The rabbit APD is
almost 5 fold longer than the rat APD; therefore the electrically equivalent tissue in
rabbit would be 5 times larger than that of the rat. However, the normal rabbit heart
is only about 2 times larger than the rat heart. This indicates that the rabbit heart
has a shorter available path length (than rat) for reentry propagation, which explains
why WoV values are smaller in the rabbit model comparing to those in the rat model
(for example, compare values in Fig. 5.8 with Fig. 5.9). The difference in arrhythmia
vulnerability between species is thus related to the relationship between physical size
and wavelength (i.e., electrical equivalent size) being different in the two species. In
the rabbit model, the ratio between physical size and wavelength is smaller than the
same ratio in the rat model.
Comparing Fig. 5.8 and Fig. 5.9, it may be noted that the WoV was decreased
in the rat diabetic model but significantly increased in the rabbit model comparing
to corresponding healthy models. The different effect of diabetes on vulnerability to
arrhythmia cannot be discussed in terms of different available electrical path lengths
in the models. However, one possible explanation may be related to the differences in
the shape and duration of action potentials in rat and rabbit. The Negative gradient
of APD restitution curve in the rat model is one of the main differences between
112
the rat and the rabbit model. The S1S2 restitution curve provided in Figure 5.11,
shows that smaller DI in the rat model results in longer APD. Therefore, when the S2
delay increases, APD shortens and therefore does the wavelength. Short wavelength
increases the chances of the reentry to propagate and therefore results in larger WoV.
In the rabbit, the restitution curve is more similar to that of the human model.
Rabbit action potential has a well-defined plateau phase while the rat model lacks
the plateau phase during repolarization. The action potential of the rabbit is longer
and its restitution curve is more similar to the human action potential and therefore
the results from rabbit model may be more likely to agree with clinical data [104].
It can be seen from Figure 5.11(a) that the APD difference between healthy and
diabetic rat models is nearly constant for all DIs. However, the APD difference
is smaller when shorter DI was used in the rabbit model (see Figure 5.11(b)). As
discussed before, prolongation of the AP opposes reentry initiation by increasing the
wavelength and on the other hand, AP shortening is in favor of larger WoV. Therefore,
in the diabetic rabbit model, APD prolongation due to diabetes for shorter DIs is
less than APD prolongation in higher DIs (diabetic restitution curve is closer to the
healthy curve in smaller DIs). This may result in relatively earlier initiation of the
reentry in diabetic rabbit model. However, Figure 5.11 cannot completely explain
why diabetes has different effects on the WoV in the rat and the rabbit models.
Another explanation for the difference between rat and rabbit models may be
that the reduced conduction reserve in rat is not as much as that of rabbit models.
This hypothesis was ruled out by Fig.5.10. There is no difference between conduction
reserve of rabbit and rat as shown in Fig.5.10. The effect of prolongation of APD
and reduced conductivity in diabetic rat combined together is not as effective as the
prolongation of diabetic rabbit APD.
113
5.4.5 Study limitations
Our model is a 2D model. Results may vary when considering 3D tissue with intramural fiber rotation. The time resolution of our simulations were 1ms and in some
cases (rabbit model with no IKATP and no uncoupling) a reentry can be missed if
happens between the time intervals. However, the WoV is not more than 2ms in
these cases.
114
Chapter 6
Conclusion
The goal of this research was divided into two main topics. The first was modelling
the effects of cardiac fiber rotation on measurement of cardiac characteristics. The
second was to investigate the effect of diabetes on vulnerability to arrhythmia in
different species. This chapter will summarize the new findings of this thesis, their
significance, study limitations, and possible future expansion of the research.
6.1 Significant findings
6.1.1 Cardiac measurements
In the first part of the thesis, the effects of fiber rotation on epicardial surface wave
propagation was modelled and it was showed that the angle of wave propagation on
the epicardial surface is not aligned with fiber orientation. This caused an error in
the conventional measurement methods of cardiac characteristics such as conduction
velocity and anisotropy ratio. Our simulations and experiments show that the angle
of propagation varies with time. This was the first study to demonstrate this effect
with both simulations and experimental recordings.
If cardiac activity is recorded by optical mapping, the recorded measurements are
more inaccurate due to effects of optical mapping caused by depth averaging and
photon scattering. We modelled the effects of OM and compared the results when
no OM was considered. We showed that the error in thicker tissues is mainly due to
OM while the error in thin tissues is mainly due to fiber rotation.
115
To improve the measurements, alternative methods were proposed based on the
conduction velocities of the propagation in the longitudinal and transverse directions.
In order to measure AR, two proposed methods (θl /θt and θmax /θmin ) were simulated
besides the conventional ellipse fitting method. The θmax /θmin method improved the
AR measurement significantly and resulted in more accurate measurements.
In order to estimate epicardial fiber orientation, it is convenient to fit an ellipse
to the propagation wavefront and consider the major axis of the ellipse as the fiber
orientation on the epicardial surface. However simulations suggested that, specially
for thin tissues, this method can result in significant measurement errors as large as
30 degrees for 1mm thick tissue. The θmax proposed method reduced this error to less
than 10 degrees for the thinnest tissue in simulation data.
6.1.2 Diabetes and arrhythmia vulnerability
In chapter 5, a mathematical model was developed for the diabetic rabbit ventricular
cell. This model was developed based on the previous healthy rabbit mathematical
model from Mahajan et al [96]. Relevant parameters were altered based on the
experimental results from diabetic rabbits [67, 93]. Our developed mathematical
diabetic rabbit model is the first model of diabetic rabbit and is well suited with
experimental data. Simulated AP from our model is similar to recorded APs from
diabetic rabbits.
Connexin lateralization in the tissue was modelled by changing the conductivity
values in the model. Our results indicated that the vulnerability to reentrant arrhythmia is reduced in diabetic rat models which was seen in the literature. To our
knowledge this is the first modelling study on connexin lateralization in the diabetic
tissue. We showed that the window of vulnerability was increased in the diabetic rab116
bit suggesting that diabetic rabbits are more prone to reentrant arrhythmia. These
novel simulation findings were in agreement with experimental literature. We did not
observe any differences in conduction reserve between rat and rabbit models. This
showed that although vulnerability to arrhythmia is species-dependent, the reason
for different behaviours in diabetic rats and rabbits is not related to the conduction
reserve.
We added a model of ATP dependent potassium current to our models and studied
the effect of IKATP opening in the context of diabetes. Our results suggested that
diabetic tissue is more prone to reentrant arrhythmia when ischemia occurs and results
in IKATP opening.
Spontaneous calcium release (SCR) is another arrhythmogenic phenomenon can
increase the vulnerability to arrhythmia. We combined spontaneous release current
with connexin lateralization alongside the changes in diabetic single cell together for
the first time. Our results, however, showed there is no difference in the propagation
of the released calcium current in the tissue.
6.2 Clinical relevance
Measurement of cardiac conduction velocity provides valuable functional and structural insights into the initiation and maintenance of cardiac arrhythmia in both clinical and experimental contexts. The knowledge gained from our approaches to measure
CV and anisotropy could have important implication for measurement techniques that
can lead to therapeutic interventions in cardiac arrhythmia.
Clinical importance of our study on the effect of diabetes on vulnerability to
arrhythmia can be better understood by knowing that diabetes is a powerful and
117
independent risk factor for cardiovascular mortality and morbidity. Cardiovascular
disease accounts for 80% of all deaths among North American patients with diabetes
[105]. Many clinical observations suggest that increased susceptibility to ventricular
arrhythmia and sudden cardiac death contribute to the increased cardiovascular mortality in patients with diabetes [106]. Our simulation results highlighted the different
effects of diabetes on different species. The human AP is more similar to the rabbit
AP than the rat AP. The results of this study can improve the understanding of
reentrant activity in the heart and the main reasons why rat experiments appear to
contradict clinical data. Our developed mathematical AP model of diabetic rabbit
can be used to extend the studies on diabetes in rabbit cardiac models which have
more similar behaviors to human heart.
6.3 Modelling limitations and future work
One of the main limitations of this study is related to the large computational cost of
running the simulations. In the first part of the thesis, the simulations were run for
different tissue slab sizes and thicknesses. One run of monodomain simulations for
1cm×1cm×1cm tissue lasted almost 80 hours on high-performance hardware with 16
processors (See Appendix A).
Our simulations in the first part of the thesis was run on rectangular slabs with
different thicknesses. Our simulations did not include tissue curvature that has been
shown to affect activation wavefront [35] and conduction velocity measurements [38].
Our ventricular models (rabbit and rat) lack fine anatomical heart structures such
as endocardial trabeculae and papillary muscles insertions. Some experimental studies
have observed reentrant activities around these areas leading to VF [107].
118
Our single cell models lack a network of calcium release units (CRUs) and ryanodine receptor network (RyR) in the membrane. This is relevant to this study as
RyR network coupling is known to affect the probability of a calcium spark to occur
in a CRU and propagate as calcium release in a cell [108, 109]. However, taking into
account CRUs in the single cell models and the stochasticity of the RyR networks, is
excessively computationally costly and is not feasible for this work.
6.4 Future work
Future work can be conducted on experimental and mathematical studies of the effect
of diabetes on the parameters of the stochastic model of SCR. Incorporating diabetes
and the stochastic nature of calcium release allows to investigate the effect of diabetes
on the probability of SRC-induced reentrant activities, source-sink relationship, and
SCR-induced DADs.
Detailed electrophysiological models such as RyR network gating and CRUs of the
single cell level can be added to this study, as well as realistic tissue characteristics
such as cell-to-cell connection morphology, fibrosis, and connexin formation on the
cell as a possible future study.
All simulations in this study were monodomain. Bidomain modelling will not
change the overall conclusions of this study. However, it can be used if the effects of
external stimulation and electrical pacemakers is desired.
It would be ideal to combine two studies —presented in this thesis— together
and expand the simulations to the whole heart level. This can help to understand
the effect of diabetes and connexin lateralization combined with the effects of fiber
rotation on the vulnerability to arrhythmia in different species. Ultimately, the aim
119
of a realistic cardiac modeling is to develop a whole heart model which can simulate
electrical activity of the heart as well as mechanical contraction based on the calcium
dynamics. Physiological structure of the heart such as fiber rotaion, Purkinje system,
endocardial trabecula has to be taken into account as well as mechanical deformations
leading to muscle contraction and blood pumping. Most obviously this requires a
team of experts in each field and to date, computational resources required for such
a complete model are not easily available.
120
Bibliography
[1] F. Martini, Fundamentals of Anatomy and Physiology. San Francisco: Pearson
Education Inc., 2004.
[2] R. S. Tubbs, M. Loukas, M. M. Shoja, M. R. Ardalan, and W. J. Oakes,
“Richard Lower (1631-1691) and his early contributions to cardiology.,” International journal of cardiology, vol. 128, pp. 17–21, aug 2008.
[3] B. Lüderitz, “Carl Friedrich Wilhelm Ludwig (1816-1895).,” Journal of interventional cardiac electrophysiology : an international journal of arrhythmias
and pacing, vol. 11, pp. 221–2, dec 2004.
[4] D. D. Streeter, H. M. Spotnitz, D. P. Patel, J. Ross, and E. H. Sonnenblick,
“Fiber orientation in the canine left ventricle during diastole and systole.,”
Circulation research, vol. 24, no. 3, pp. 339–347, 1969.
[5] J. B. Caulfield and T. K. Borg, “The collagen network of the heart.,” Laboratory
investigation; a journal of technical methods and pathology, vol. 40, pp. 364–72,
mar 1979.
[6] I. J. LeGrice, B. H. Smaill, L. Z. Chai, S. G. Edgar, J. B. Gavin, and P. J.
Hunter, “Laminar structure of the heart: ventricular myocyte arrangement and
connective tissue architecture in the dog.,” The American journal of physiology,
vol. 269, pp. H571–82, aug 1995.
[7] D. F. Scollan, a. Holmes, J. Zhang, and R. L. Winslow, “Reconstruction of
cardiac ventricular geometry and fiber orientation using magnetic resonance
imaging.,” Annals of biomedical engineering, vol. 28, pp. 934–44, aug 2000.
121
[8] K. Willecke, J. Eiberger, J. Degen, D. Eckardt, A. Romualdi, M. Güldenagel,
U. Deutsch, and G. Söhl, “Structural and Functional Diversity of Connexin
Genes in the Mouse and Human Genome,” Biological Chemistry, vol. 383, jan
2002.
[9] N. J. Severs, A. F. Bruce, E. Dupont, and S. Rothery, “Remodelling of gap
junctions and connexin expression in diseased myocardium.,” Cardiovascular
research, vol. 80, pp. 9–19, oct 2008.
[10] D. M. Bers, “Cardiac excitationcontraction coupling,” Nature, vol. 415, pp. 198–
205, jan 2002.
[11] J. N. Weiss, A. Garfinkel, H. S. Karagueuzian, P. S. Chen, and Z. Qu, “Early
afterdepolarizations and cardiac arrhythmias,” Heart Rhythm, vol. 7, no. 12,
pp. 1891–1899, 2010.
[12] a. O. Verkerk, M. W. Veldkamp, A. Baartscheer, C. a. Schumacher, C. Klopping,
a. C. van Ginneken, J. H. Ravesloot, C. Klöpping, a. C. van Ginneken, and J. H.
Ravesloot, “Ionic Mechanism of Delayed Afterdepolarizations in Ventricular
Cells Isolated From Human End-Stage Failing Hearts,” Circulation, vol. 104,
no. 22, pp. 2728–2733, 2001.
[13] J. L. Smeets, M. a. Allessie, W. J. Lammers, F. I. Bonke, and J. Hollen, “The
wavelength of the cardiac impulse and reentrant arrhythmias in isolated rabbit atrium. The role of heart rate, autonomic transmitters, temperature, and
potassium.,” Circulation research, vol. 58, no. 1925, pp. 96–108, 1986.
[14] D. Sato, L.-H. Xie, A. a. Sovari, D. X. Tran, N. Morita, F. Xie, H. Karagueuzian,
A. Garfinkel, J. N. Weiss, and Z. Qu, “Synchronization of chaotic early after122
depolarizations in the genesis of cardiac arrhythmias.,” Proceedings of the National Academy of Sciences of the United States of America, vol. 106, no. 9,
pp. 2983–2988, 2009.
[15] M. A. Atkinson and G. S. Eisenbarth, “Type 1 diabetes: new perspectives
on disease pathogenesis and treatment.,” Lancet (London, England), vol. 358,
pp. 221–9, jul 2001.
[16] T. R. Harrison and D. L. Kasper, Harrison’s principles of internal medicine.
New York: McGraw-Hill, Medical Pub. Division., 18 ed., 2005.
[17] K. Abo, Y. Ishida, R. Yoshida, T. Hozumi, H. Ueno, H. Shiotani, K. Matsunaga,
and T. Kazumi, “Torsade de pointes in NIDDM with long QT intervals.,” Diabetes care, vol. 19, p. 1010, sep 1996.
[18] T. Inoguchi, H. Y. Yu, M. Imamura, M. Kakimoto, T. Kuroki, T. Maruyama,
and H. Nawata, “Altered gap junction activity in cardiovascular tissues of diabetes.,” Medical electron microscopy : official journal of the Clinical Electron
Microscopy Society of Japan, vol. 34, pp. 86–91, jun 2001.
[19] L. Okruhlicova, N. Tribulova, M. Misejkova, M. Kucka, R. Stetka, J. Slezak, and
M. Manoach, “Gap junction remodelling is involved in the susceptibility of diabetic rats to hypokalemia-induced ventricular fibrillation.,” Acta histochemica,
vol. 104, no. 4, pp. 387–91, 2002.
[20] D. Qin, B. Huang, L. Deng, H. El-Adawi, K. Ganguly, J. R. Sowers, and N. ElSherif, “Downregulation of K(+) channel genes expression in type I diabetic cardiomyopathy.,” Biochemical and biophysical research communications, vol. 283,
pp. 549–53, may 2001.
123
[21] A. Nygren, M. L. Olson, K. Y. Chen, T. Emmett, G. Kargacin, and Y. Shimoni, “Propagation of the cardiac impulse in the diabetic rat heart: reduced
conduction reserve.,” The Journal of physiology, vol. 580, pp. 543–60, apr 2007.
[22] J. H. Smith, C. R. Green, N. S. Peters, S. Rothery, and N. J. Severs, “Altered patterns of gap junction distribution in ischemic heart disease. An immunohistochemical study of human myocardium using laser scanning confocal
microscopy.,” The American journal of pathology, vol. 139, no. 4, pp. 801–821,
1991.
[23] M. Uzzaman, H. Honjo, Y. Takagishi, L. Emdad, a. I. Magee, N. J. Severs,
and I. Kodama, “Remodeling of gap junctional coupling in hypertrophied right
ventricles of rats with monocrotaline-induced pulmonary hypertension.,” Circulation research, vol. 86, no. 8, pp. 871–8, 2000.
[24] N. S. Peters, J. Coromilas, N. J. Severs, and A. L. Wit, “Disturbed Connexin43
Gap Junction Distribution Correlates With the Location of Reentrant Circuits
in the Epicardial Border Zone of Healing Canine Infarcts That Cause Ventricular Tachycardia,” Circulation, vol. 95, pp. 988–996, feb 1997.
[25] S. Kostin, M. Rieger, S. Dammer, S. Hein, M. Richter, W.-P. Klövekorn,
E. P. Bauer, and J. Schaper, “Gap junction remodeling and altered connexin43
expression in the failing human heart.,” Molecular and cellular biochemistry,
vol. 242, pp. 135–44, jan 2003.
[26] S. Kostin, S. Dammer, S. Hein, W. P. Klovekorn, E. P. Bauer, and J. Schaper,
“Connexin 43 expression and distribution in compensated and decompensated
cardiac hypertrophy in patients with aortic stenosis.,” Cardiovascular research,
124
vol. 62, pp. 426–36, may 2004.
[27] R. R. Kaprielian, M. Gunning, E. Dupont, M. N. Sheppard, S. M. Rothery,
R. Underwood, D. J. Pennell, K. Fox, J. Pepper, P. a. Poole-Wilson, and N. J.
Severs, “Downregulation of immunodetectable connexin43 and decreased gap
junction size in the pathogenesis of chronic hibernation in the human left ventricle.,” Circulation, vol. 97, no. 7, pp. 651–60, 1998.
[28] N. J. Severs, S. R. Coppen, E. Dupont, H.-I. Yeh, Y.-S. Ko, and T. Matsushita,
“Gap junction alterations in human cardiac disease,” Cardiovascular Research,
vol. 62, no. 2, pp. 368–377, 2004.
[29] E. Dupont, T. Matsushita, R. a. Kaba, C. Vozzi, S. R. Coppen, N. Khan,
R. Kaprielian, M. H. Yacoub, and N. J. Severs, “Altered connexin expression in
human congestive heart failure.,” Journal of molecular and cellular cardiology,
vol. 33, pp. 359–71, feb 2001.
[30] S. Rush and H. Larsen, “A practical algorithm for solving dynamic membrane equations,” IEEE transactions on bio-medical engineering, vol. 25, no. 4,
pp. 389–92, 1978.
[31] Z. Chen, Finite Element Methods and Their Applications. Springer-Verlag
Berlin Heidelberg, 2005.
[32] E. J. Vigmond, M. Hughes, G. Plank, and L. Leon, “Computational tools
for modeling electrical activity in cardiac tissue,” Journal of Electrocardiology,
vol. 36, pp. 69–74, dec 2003.
[33] A. Ghazanfari, E. Vigmond, and A. Nygren, “Cardiac fiber rotation distorts
125
surface measurements of anisotropic propagation.,” Conference proceedings : ...
Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference,
vol. 2012, pp. 685–8, aug 2012.
[34] a. Ghazanfari, M. P. Rodriguez, E. Vigmond, and a. Nygren, “Computer simulation of cardiac propagation: effects of fiber rotation, intramural conductivity,
and optical mapping.,” IEEE transactions on bio-medical engineering, vol. 61,
no. 7, pp. 2041–8, 2014.
[35] C. S. Henriquez, a. L. Muzikant, and C. K. Smoak, “Anisotropy, fiber curvature, and bath loading effects on activation in thin and thick cardiac tissue
preparations: simulations in a three-dimensional bidomain model.,” Journal of
cardiovascular electrophysiology, vol. 7, pp. 424–44, may 1996.
[36] M. Stein, T. a. B. van Veen, R. N. W. Hauer, J. M. T. de Bakker, and H. V. M.
van Rijen, “A 50% reduction of excitability but not of intercellular coupling
affects conduction velocity restitution and activation delay in the mouse heart.,”
PloS one, vol. 6, p. e20310, jan 2011.
[37] M. Stein, T. a. B. van Veen, C. A. Remme, M. Boulaksil, M. Noorman, L. van
Stuijvenberg, R. van der Nagel, C. R. Bezzina, R. N. W. Hauer, J. M. T.
de Bakker, and H. V. M. van Rijen, “Combined reduction of intercellular coupling and membrane excitability differentially affects transverse and longitudinal cardiac conduction.,” Cardiovascular research, vol. 83, pp. 52–60, jul 2009.
[38] E. B. Bourgeois, V. G. Fast, R. L. Collins, J. D. Gladden, and J. M. Rogers,
“Change in conduction velocity due to fiber curvature in cultured neonatal rat
126
ventricular myocytes.,” IEEE transactions on bio-medical engineering, vol. 56,
pp. 855–61, mar 2009.
[39] C. J. Hyatt, C. W. Zemlin, R. M. Smith, A. Matiukas, A. M. Pertsov, and
O. Bernus, “Reconstructing subsurface electrical wave orientation from cardiac
epi-fluorescence recordings: Monte Carlo versus diffusion approximation.,” Optics express, vol. 16, pp. 13758–72, sep 2008.
[40] A. E. Pollard, M. J. Burgess, and K. W. Spitzer, “Computer simulations of
three-dimensional propagation in ventricular myocardium. Effects of intramural fiber rotation and inhomogeneous conductivity on epicardial activation,”
Circulation Research, vol. 72, pp. 744–756, apr 1993.
[41] E. W. Hsu, A. L. Muzikant, S. A. Matulevicius, R. C. Penland, and C. S. Henriquez, “Magnetic resonance myocardial fiber-orientation mapping with direct
histological correlation.,” American Journal of Physiology, vol. 274, no. 5 Pt 2,
pp. H1627–H1634, 1998.
[42] D. Roberts, L. Hersh, and A. Scher, “Influence of cardiac fiber orientation
on wavefront voltage, conduction velocity, and tissue resistivity in the dog,”
Circulation research, vol. 44, no. 5, pp. 701–712, 1979.
[43] B. Taccardi, B. B. Punske, E. Macchi, R. S. Macleod, and P. R. Ershler, “Epicardial and intramural excitation during ventricular pacing: effect of myocardial
structure.,” American journal of physiology. Heart and circulatory physiology,
vol. 294, pp. H1753–66, apr 2008.
[44] B. Taccardi, E. Macchi, R. L. Lux, P. R. Ershler, S. Spaggiari, S. Baruffi, and
Y. Vyhmeister, “Effect of myocardial fiber direction on epicardial potentials,”
127
Circulation, vol. 90, pp. 3076–3090, dec 1994.
[45] A. Nygren, R. B. Clark, D. D. Belke, C. Kondo, W. R. Giles, and F. X.
Witkowski, “Voltage-sensitive dye mapping of activation and conduction in
adult mouse hearts.,” Annals of biomedical engineering, vol. 28, pp. 958–67,
aug 2000.
[46] A. Nygren, C. Kondo, R. B. Clark, and W. R. Giles, “Voltage-sensitive dye
mapping in Langendorff-perfused rat hearts.,” American journal of physiology.
Heart and circulatory physiology, vol. 284, pp. H892–902, mar 2003.
[47] S. B. Knisley, “Optical mapping of cardiac electrical stimulation.,” Journal of
electrocardiology, vol. 30 Suppl, pp. 11–8, jan 1998.
[48] M. J. Bishop, B. Rodriguez, J. Eason, J. P. Whiteley, N. Trayanova, and
D. J. Gavaghan, “Synthesis of voltage-sensitive optical signals: application to
panoramic optical mapping.,” Biophysical journal, vol. 90, pp. 2938–45, apr
2006.
[49] M. J. Bishop, B. Rodriguez, F. Qu, I. R. Efimov, D. J. Gavaghan, and N. a.
Trayanova, “The role of photon scattering in optical signal distortion during
arrhythmia and defibrillation.,” Biophysical journal, vol. 93, pp. 3714–26, nov
2007.
[50] W.-C. Li, S. R. Soffe, and A. Roberts, “A direct comparison of whole cell patch
and sharp electrodes by simultaneous recording from single spinal neurons in
frog tadpoles.,” Journal of neurophysiology, vol. 92, no. 1, pp. 380–386, 2004.
[51] S. V. Pandit, R. B. Clark, W. R. Giles, and S. S. Demir, “A mathematical
128
model of action potential heterogeneity in adult rat left ventricular myocytes.,”
Biophysical journal, vol. 81, pp. 3029–51, dec 2001.
[52] P. Colli Franzone, L. F. Pavarino, and B. Taccardi, “Effects of transmural electrical heterogeneities and electrotonic interactions on the dispersion of cardiac
repolarization and action potential duration: A simulation study.,” Mathematical biosciences, vol. 204, pp. 132–65, nov 2006.
[53] P. Colli Franzone, L. F. Pavarino, and B. Taccardi, “Monodomain simulations
of excitation and recovery in cardiac blocks with intramural heterogeneity,”
Functional Imaging and Modeling . . . , pp. 267–277, 2005.
[54] O. Bernus, M. Wellner, and a. Pertsov, “Intramural wave propagation in cardiac
tissue: Asymptotic solutions and cusp waves,” Physical Review E, vol. 70, pp. 1–
7, dec 2004.
[55] G. E. Morley, D. Vaidya, and J. Jalife, “Characterization of conduction in
the ventricles of normal and heterozygous Cx43 knockout mice using optical
mapping.,” Journal of cardiovascular electrophysiology, vol. 11, pp. 375–7, mar
2000.
[56] P. V. Bayly, B. H. KenKnight, J. M. Rogers, R. E. Hillsley, R. E. Ideker, and
W. M. Smith, “Estimation of conduction velocity vector fields from epicardial
mapping data.,” IEEE transactions on bio-medical engineering, vol. 45, pp. 563–
71, may 1998.
[57] N. Mazeh, D. E. Haines, M. W. Kay, and B. J. Roth, “A Simplified Approach
for Simultaneous Measurements of Wavefront Velocity and Curvature in the
129
Heart Using Activation Times,” Cardiovascular Engineering and Technology,
vol. 4, pp. 520–534, jun 2013.
[58] M. W. Kay and R. a. Gray, “Measuring curvature and velocity vector fields for
waves of cardiac excitation in 2-D media.,” IEEE transactions on bio-medical
engineering, vol. 52, pp. 50–63, jan 2005.
[59] D. Janks and B. Roth, “Averaging Over Depth During Optical Mapping of
Unipolar Stimulation,” Biomedical Engineering, IEEE . . . , vol. 49, no. 9,
pp. 1051–1054, 2002.
[60] W. T. Baxter, S. F. Mironov, a. V. Zaitsev, J. Jalife, and a. M. Pertsov, “Visualizing excitation waves inside cardiac muscle using transillumination.,” Biophysical journal, vol. 80, pp. 516–30, jan 2001.
[61] A. Ghazanfari, E. Vigmond, and A. Nygren, “Cardiac fiber rotation distorts
surface measurements of anisotropic propagation.,” Conference proceedings : ...
Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference,
vol. 2012, pp. 685–8, aug 2012.
[62] B. J. Roth and A. M. Pertsov, “Hybrid modeling of electrical and optical behavior in the heart,” Physica D-Nonlinear Phenomena, vol. 238, no. 11-12,
pp. 1019–1027, 2009.
[63] R. D. Walton, D. Benoist, C. J. Hyatt, S. H. Gilbert, E. White, and O. Bernus,
“Dual excitation wavelength epifluorescence imaging of transmural electrophysiological properties in intact hearts.,” Heart rhythm : the official journal of the
Heart Rhythm Society, vol. 7, pp. 1843–9, dec 2010.
130
[64] O. Casis, M. Gallego, M. Iriarte, and J. a. Sánchez-Chapula, “Effects of diabetic
cardiomyopathy on regional electrophysiologic characteristics of rat ventricle.,”
Diabetologia, vol. 43, no. 1, pp. 101–109, 2000.
[65] Y. Shimoni, L. Firek, D. Severson, and W. Giles, “Short-term diabetes alters
K+ currents in rat ventricular myocytes.,” Circulation research, vol. 74, no. 4,
pp. 620–628, 1994.
[66] H. J. Whittington, G. G. Babu, M. M. Mocanu, D. M. Yellon, and D. J. Hausenloy, “The diabetic heart: too sweet for its own good?,” Cardiology research and
practice, vol. 2012, p. 845698, jan 2012.
[67] Y. Zhang, J. Xiao, H. Lin, X. Luo, and H. Wang, “Ionic mechanisms underlying
abnormal QT prolongation and the associated arrhythmias in diabetic rabbits:
a role of rapid delayed rectifier K+ current,” Cellular Physiology and . . . , 2007.
[68] J. R. Erickson, L. Pereira, L. Wang, G. Han, A. Ferguson, K. Dao, R. J.
Copeland, F. Despa, G. W. Hart, C. M. Ripplinger, and D. M. Bers, “Diabetic
hyperglycaemia activates CaMKII and arrhythmias by O-linked glycosylation.,”
Nature, vol. 502, pp. 372–6, oct 2013.
[69] Z. Y. Fang, J. B. Prins, and T. H. Marwick, “Diabetic cardiomyopathy: evidence, mechanisms, and therapeutic implications.,” Endocrine reviews, vol. 25,
no. 4, pp. 543–567, 2004.
[70] D. Ebel, J. Müllenheim, J. Frässdorf, A. Heinen, R. Huhn, T. Bohlen, J. Ferrari,
H. Südkamp, B. Preckel, W. Schlack, and V. Thämer, “Effect of acute hyperglycaemia and diabetes mellitus with and without short-term insulin treatment on
131
myocardial ischaemic late preconditioning in the rabbit heart in vivo.,” Pflügers
Archiv : European journal of physiology, vol. 446, pp. 175–82, may 2003.
[71] D. J. Lefer, R. Scalia, S. P. Jones, B. R. Sharp, M. R. Hoffmeyer, a. R. Farvid,
M. F. Gibson, and a. M. Lefer, “HMG-CoA reductase inhibition protects the
diabetic myocardium from ischemia-reperfusion injury.,” The FASEB journal
: official publication of the Federation of American Societies for Experimental
Biology, vol. 15, no. 8, pp. 1454–1456, 2001.
[72] H. Su, X. Sun, H. Ma, H.-F. Zhang, Q.-J. Yu, C. Huang, X.-M. Wang, R.-H.
Luan, G.-L. Jia, H.-C. Wang, and F. Gao, “Acute hyperglycemia exacerbates
myocardial ischemia/reperfusion injury and blunts cardioprotective effect of
GIK.,” American journal of physiology. Endocrinology and metabolism, vol. 293,
no. 3, pp. E629–E635, 2007.
[73] M. Desrois, K. Clarke, C. Lan, C. Dalmasso, M. Cole, B. Portha, P. J. Cozzone,
and M. Bernard, “Upregulation of eNOS and unchanged energy metabolism
in increased susceptibility of the aging type 2 diabetic GK rat heart to ischemic injury.,” American journal of physiology. Heart and circulatory physiology, vol. 299, no. 5, pp. H1679–H1686, 2010.
[74] A. a. Bulhak, C. Jung, C.-G. Ostenson, J. O. Lundberg, P.-O. Sjöquist, and
J. Pernow, “PPAR-alpha activation protects the type 2 diabetic myocardium
against ischemia-reperfusion injury: involvement of the PI3-Kinase/Akt and
NO pathway.,” American journal of physiology. Heart and circulatory physiology, vol. 296, no. 3, pp. H719–H727, 2009.
[75] G. Ma, M. Al-Shabrawey, J. a. Johnson, R. Datar, H. E. Tawfik, D. Guo,
132
R. B. Caldwell, and R. W. Caldwell, “Protection against myocardial ischemia/reperfusion injury by short-term diabetes: enhancement of VEGF formation, capillary density, and activation of cell survival signaling.,” NaunynSchmiedeberg’s archives of pharmacology, vol. 373, pp. 415–27, sep 2006.
[76] S. Matsumoto, S. Cho, S. Tosaka, H. Ureshino, T. Maekawa, T. Hara, and
K. Sumikawa, “Pharmacological preconditioning in type 2 diabetic rat hearts:
The roles of mitochondrial atp-sensitive potassium channels and the phosphatidylinositol 3-kinase-akt pathway,” Cardiovascular Drugs and Therapy,
vol. 23, no. 4, pp. 263–270, 2009.
[77] T. Ravingerová, A. Adameová, J. Matejı́ková, T. Kelly, M. Nemčeková,
J. Kucharská, O. Pecháová, and A. Lazou, “Subcellular mechanisms of adaptation in the diabetic myocardium: Relevance to ischemic preconditioning in
the nondiseased heart.,” Experimental and clinical cardiology, vol. 15, no. 4,
pp. 68–76, 2010.
[78] T. Ravingerova, R. Stetka, and D. Pancza, “Susceptibility to ischemia-induced
arrhythmias and the effect of preconditioning in the diabetic rat heart,” Physiological . . . , 2000.
[79] T. Ravingerova, J. Neckar, F. Kolar, R. Stetka, K. Volkovova, A. Ziegelhöffer,
and J. Styk, “Ventricular arrhythmias following coronary artery occlusion in
rats: Is the diabetic heart less or more sensitive to ischaemia?,” Basic Research
in Cardiology, vol. 96, no. 2, pp. 160–168, 2001.
[80] A. Tsang, D. J. Hausenloy, M. M. Mocanu, R. D. Carr, and D. M. Yellon,
“Preconditioning the Diabetic Heart: The Importance of Akt Phosphorylation,”
133
Diabetes, vol. 54, pp. 2360–2364, aug 2005.
[81] S. B. Kristiansen, B. Løfgren, N. B. Støttrup, D. Khatir, J. E. Nielsen-Kudsk,
T. T. Nielsen, H. E. Bøtker, and a. Flyvbjerg, “Ischaemic preconditioning does
not protect the heart in obese and lean animal models of Type 2 diabetes,”
Diabetologia, vol. 47, no. 10, pp. 1716–1721, 2004.
[82] L. M. Chu, R. M. Osipov, M. P. Robich, J. Feng, S. Oyamada, C. Bianchi, and
F. W. Sellke, “Is hyperglycemia bad for the heart during acute ischemia?,” The
Journal of thoracic and cardiovascular surgery, vol. 140, pp. 1345–52, dec 2010.
[83] A. Noma, “ATP-regulated K+ channels in cardiac muscle.,” Nature, vol. 305,
pp. 147–148, sep 1983.
[84] R. M. Shaw and Y. Rudy, “Electrophysiologic effects of acute myocardial ischemia: a theoretical study of altered cell excitability and action potential
duration.,” Cardiovascular research, vol. 35, no. 2, pp. 256–272, 1997.
[85] B. I. Sasyniuk, “Concept of reentry versus automaticity,” The American Journal of Cardiology, vol. 54, pp. A1–A6, jul 1984.
[86] D. G. Katritsis and a. J. Camm, “Atrioventricular nodal reentrant tachycardia,”
Circulation, vol. 122, no. 8, pp. 831–840, 2010.
[87] F. G. Akar, D. D. Spragg, R. S. Tunin, D. a. Kass, and G. F. Tomaselli, “Mechanisms underlying conduction slowing and arrhythmogenesis in nonischemic dilated cardiomyopathy,” Circulation Research, vol. 95, no. 7, pp. 717–725, 2004.
[88] N. Zeevi-Levin, Y. D. Barac, Y. Reisner, I. Reiter, G. Yaniv, G. Meiry,
Z. Abassi, S. Kostin, J. Schaper, M. R. Rosen, N. Resnick, and O. Binah,
134
“Gap junctional remodeling by hypoxia in cultured neonatal rat ventricular
myocytes,” Cardiovascular Research, vol. 66, no. 1, pp. 64–73, 2005.
[89] E. De Vuyst, K. Boengler, G. Antoons, K. R. Sipido, R. Schulz, and L. Leybaert, “Pharmacological modulation of connexin-formed channels in cardiac
pathophysiology,” British Journal of Pharmacology, vol. 163, no. 3, pp. 469–
483, 2011.
[90] S. Kanno and J. E. Saffitz, “The role of myocardial gap junctions in electrical conduction and arrhythmogenesis.,” Cardiovascular pathology : the official
journal of the Society for Cardiovascular Pathology, vol. 10, no. 4, pp. 169–77,
2001.
[91] T. Seidel, A. Salameh, and S. Dhein, “A simulation study of cellular hypertrophy and connexin lateralization in cardiac tissue.,” Biophysical journal, vol. 99,
pp. 2821–30, nov 2010.
[92] G. N. Pierce and J. C. Russell, “Regulation of intracellular Ca2+ in the heart
during diabetes,” Cardiovascular Research, vol. 34, no. 1, pp. 41–47, 1997.
[93] K. M. Choi, Y. Zhong, B. D. Hoit, I. L. Grupp, H. Hahn, K. W. Dilly, S. Guatimosim, W. J. Lederer, and M. a. Matlib, “Defective intracellular Ca(2+) signaling contributes to cardiomyopathy in Type 1 diabetic rats.,” American journal
of physiology. Heart and circulatory physiology, vol. 283, no. 4, pp. H1398–
H1408, 2002.
[94] A. Varró, D. A. Lathrop, S. B. Hester, P. P. Nánási, and J. G. Papp, “Ionic currents and action potentials in rabbit, rat, and guinea pig ventricular myocytes.,”
Basic research in cardiology, vol. 88, no. 2, pp. 93–102, 1993.
135
[95] S. V. Pandit, W. R. Giles, and S. S. Demir, “A mathematical model of the
electrophysiological alterations in rat ventricular myocytes in type-I diabetes.,”
Biophysical journal, vol. 84, pp. 832–41, mar 2003.
[96] A. Mahajan, Y. Shiferaw, D. Sato, A. Baher, R. Olcese, L.-H. Xie, M.-J. Yang,
P.-S. Chen, J. G. Restrepo, A. Karma, A. Garfinkel, Z. Qu, and J. N. Weiss, “A
rabbit ventricular action potential model replicating cardiac dynamics at rapid
heart rates.,” Biophysical journal, vol. 94, pp. 392–410, jan 2008.
[97] Y. Xie, D. Sato, A. Garfinkel, Z. Qu, and J. N. Weiss, “So little source, so much
sink: requirements for afterdepolarizations to propagate in tissue.,” Biophysical
journal, vol. 99, pp. 1408–15, sep 2010.
[98] L. Clerc, “Directional differences of impulse spread in trabecular muscle from
mammalian heart.,” The Journal of physiology, vol. 255, no. 2, pp. 335–346,
1976.
[99] H. a. Ghaly, P. M. Boyle, E. J. Vigmond, Y. Shimoni, and A. Nygren, “Simulations of reduced conduction reserve in the diabetic rat heart: response to uncoupling and reduced excitability.,” Annals of biomedical engineering, vol. 38,
pp. 1415–25, apr 2010.
[100] R. Marfella, M. D’Amico, C. Di Filippo, E. Piegari, F. Nappo, K. Esposito,
L. Berrino, F. Rossi, and D. Giugliano, “Myocardial infarction in diabetic rats:
Role of hyperglycaemia on infarct size and early expression of hypoxia-inducible
factor 1,” Diabetologia, vol. 45, no. 8, pp. 1172–1181, 2002.
[101] A. T. Winfree, “Electrical turbulence in three-dimensional heart muscle.,” Science (New York, N.Y.), vol. 266, no. 5187, pp. 1003–1006, 1994.
136
[102] B. B. Krames and E. J. Van Liere, “The heart weight and ventricular weights
of normal adult albino rats.,” The Anatomical record, vol. 156, pp. 461–4, dec
1966.
[103] R. F. Wiegerinck, A. O. Verkerk, C. N. Belterman, T. A. B. Van Veen,
A. Baartscheer, T. Opthof, R. Wilders, J. M. T. De Bakker, and R. Coronel,
“Larger cell size in rabbits with heart failure increases myocardial conduction
velocity and QRS duration,” Circulation, vol. 113, no. 6, pp. 806–813, 2006.
[104] E. Chow, A. Bernjak, S. Williams, R. a. Fawdry, S. Hibbert, J. Freeman, P. J.
Sheridan, and S. R. Heller, “Risk of cardiac arrhythmias during hypoglycemia
in patients with type 2 diabetes and cardiovascular risk,” Diabetes, vol. 63,
no. 5, pp. 1738–1747, 2014.
[105] F. X. Pi-Sunyer, “The Mission of the American Diabetes Association: 1993
Presidential Address,” Diabetes Care, vol. 16, pp. 1521–1525, nov 1993.
[106] J. D. Curb, B. L. Rodriguez, C. M. Burchfiel, R. D. Abbott, D. Chiu, and
K. Yano, “Sudden death, impaired glucose tolerance, and diabetes in Japanese
American men.,” Circulation, vol. 91, pp. 2591–5, may 1995.
[107] M. Valderrábano, “Influence of anisotropic conduction properties in the propagation of the cardiac action potential.,” Progress in biophysics and molecular
biology, vol. 94, no. 1-2, pp. 144–68, 2007.
[108] W. Chen, J. A. Wasserstrom, and Y. Shiferaw, “Role of coupled gating between
cardiac ryanodine receptors in the genesis of triggered arrhythmias.,” Am J
Physiol Heart Circ Physiol, vol. 297, pp. H171—-H180, jul 2009.
137
[109] J. A. Wasserstrom, Y. Shiferaw, W. Chen, S. Ramakrishna, H. Patel, J. E. Kelly,
M. J. O’Toole, A. Pappas, N. Chirayil, N. Bassi, L. Akintilo, M. Wu, R. Arora,
and G. L. Aistrup, “Variability in Timing of Spontaneous Calcium Release
in the Intact Rat Heart Is Determined by the Time Course of Sarcoplasmic
Reticulum Calcium Load.,” Circulation research, sep 2010.
138
Appendix A
Simulation Time
Simulation details are provided in Table A.1. Simulations were run on sixteen processors Intel CPU 2.8 GHz, 32 GB RAM. Optical mapping simulations (OM) were run
for different tissue thickness, intramural conductivity, with and without the effect of
OM.
Simulations corresponding to measurements of the Window of Vulnerability (WoV)
were run for rat and rabbit models. For the WoV in the rat model, each bar in Figure
5.8 is derived from almost 40 runs. Figure 5.8 is derived from 24 separate set of
simulations which means almost 1000 different runs of simulations was performed to
obtain this Figure. The rabbit’s WoV simulations were run for almost 500 times but
since the rabbit tissue is larger than the rat tissue each run was almost two hours.
The total simulation time is roughly more than 3000 hours for this thesis.
139
Simulation
Tissue
Discretization
Runs
Time (hr/run)
Total (hours)
OM
1mm
50µm
4
40
160
OM
1mm
100µm
8
6
48
OM
2mm
100µm
8
15
120
OM
4mm
100µm
8
35
280
OM
10mm
100µm
8
80
640
WoV
rat
100µm
1000
1
1000
WoV
rabbit
100µm
500
2
1000
Table A.1: Simulation details: number of runs, simulation times, and total time for each
simulation. Optical mapping (OM) simulations correspond to the Table 4.2. The WoV
simulations for rat 5.8 and rabbit 5.9 were run on 1cm×1cm and 2cm×2cm 2D tissue
respectively.
140
Appendix B
141
Copyright Permissions
5/13/2016
RightsLink Printable License
NATURE PUBLISHING GROUP LICENSE
TERMS AND CONDITIONS
May 13, 2016
This is a License Agreement between Amin Ghazanfari ("You") and Nature Publishing
Group ("Nature Publishing Group") provided by Copyright Clearance Center ("CCC"). The
license consists of your order details, the terms and conditions provided by Nature
Publishing Group, and the payment terms and conditions.
All payments must be made in full to CCC. For payment instructions, please see
information listed at the bottom of this form.
License Number
3866930208211
License date
May 13, 2016
Licensed content publisher
Nature Publishing Group
Licensed content publication Nature
Licensed content title
Cardiac excitation­contraction coupling
Licensed content author
Donald M. Bers
Licensed content date
Jan 10, 2002
Volume number
415
Issue number
6868
Type of Use
reuse in a dissertation / thesis
Requestor type
academic/educational
Format
print and electronic
Portion
figures/tables/illustrations
Number of
figures/tables/illustrations
1
High­res required
no
Figures
Figure 1
Author of this NPG article
no
Your reference number
None
Title of your thesis /
dissertation
Intercellular Coupling Abnormalities In The Heart: Quantification
From Surface Measurements And Impact On Arrhythmia Vulnerability
Expected completion date
May 2016
Estimated size (number of
pages)
120
Total
0.00 CAD
Terms and Conditions
Terms and Conditions for Permissions
Nature Publishing Group hereby grants you a non­exclusive license to reproduce this
material for this purpose, and for no other use,subject to the conditions below:
https://s100.copyright.com/AppDispatchServlet
1/3
142
5/13/2016
RightsLink Printable License
NATURE PUBLISHING GROUP LICENSE
TERMS AND CONDITIONS
May 13, 2016
This is a License Agreement between Amin Ghazanfari ("You") and Nature Publishing
Group ("Nature Publishing Group") provided by Copyright Clearance Center ("CCC"). The
license consists of your order details, the terms and conditions provided by Nature
Publishing Group, and the payment terms and conditions.
All payments must be made in full to CCC. For payment instructions, please see
information listed at the bottom of this form.
License Number
3866930208211
License date
May 13, 2016
Licensed content publisher
Nature Publishing Group
Licensed content publication Nature
Licensed content title
Cardiac excitation­contraction coupling
Licensed content author
Donald M. Bers
Licensed content date
Jan 10, 2002
Volume number
415
Issue number
6868
Type of Use
reuse in a dissertation / thesis
Requestor type
academic/educational
Format
print and electronic
Portion
figures/tables/illustrations
Number of
figures/tables/illustrations
1
High­res required
no
Figures
Figure 1
Author of this NPG article
no
Your reference number
None
Title of your thesis /
dissertation
Intercellular Coupling Abnormalities In The Heart: Quantification
From Surface Measurements And Impact On Arrhythmia Vulnerability
Expected completion date
May 2016
Estimated size (number of
pages)
120
Total
0.00 CAD
Terms and Conditions
Terms and Conditions for Permissions
Nature Publishing Group hereby grants you a non­exclusive license to reproduce this
material for this purpose, and for no other use,subject to the conditions below:
https://s100.copyright.com/AppDispatchServlet
1/3
143