Download STAT 302 Axioms of Probability

STAT 302
Chapter 2
Axioms of Probability
Instructor: Natalia Nolde
Fall 2016
1
Sample Space
• Definition: A random experiment is an experiment whose outcomes
cannot be predicted with certainty
• Definition: The sample space S of a random experiment is the set of all
possible outcomes of the experiment
• Examples:
D Tossing a coin twice: S = {HH, HT , TH, TT }
D Rolling a die: S = {1, 2, 3, 4, 5, 6}
D Measuring the lifetime (in years) of a person: S = {x : 0 ≤ x ≤ ∞}
2
Events
• Definition: An event is any subset of the sample space S
D Events will be denoted by capital letters
D If the outcome of an experiment is in set E ⊂ S, then we say that
event E has occured
• Examples:
D Coin tossing: E = {TT } is the event that tail was observed on both coin
tosses
D Die rolling: E = {1, 3, 5} is the event that an odd number was observed
on the die
D Lifetime: E = {x ≥ 70} is the event that the person has lived for at least
70 years
• Note: An event with no outcome in S is the null set, denoted ∅
D E.g., if event E corresponds to rolling number ”7” on a regular dice,
then E = ∅
3
Events - more definitions and notation
• The complement of event E , denoted E c , is the set of outcomes that
are in the sample space but do not belong to E .
Note that S c = ∅.
• Given events A and B, the union of A and B, denoted A ∪ B, is the set
of all outcomes either in A or B or in both A and B.
Event A ∪ B occurs if either A or B occurs.
• Given events A and B, the intersection of A and B, denoted A ∩ B or
AB, is the set of all outcomes which lie in both A and B.
Event A ∩ B occurs if both A and B occur.
• Venn Diagram
4
• Two events A and B are said to be mutually exclusive (disjoint)
if A ∩ B = ∅
• Union of a series of events:
S∞
n=1 En
• Intersection of a series of events:
= E1 ∪ E2 ∪ E3 ∪ ....
T∞
n=1 En
= E1 ∩ E2 ∩ E3 ∩ ...
5
• Let A, B be two events in the same sample space.
If all outcomes in A are in B, we say that A is contained in B
(write A ⊂ B or B ⊃ A). The occurrence of A implies B also occurs.
D E.g. Suppose A is the event that we roll an even number and B is that
we roll a number greater than 1. Then A ⊂ B.
• If A ⊃ B and B ⊃ A, then A = B.
6
Events - Properties
• Commutative laws: E ∪ F = F ∪ E ; E ∩ F = F ∩ E
• Associative laws: (E ∪ F ) ∪ G = E ∪ (F ∪ G );
(E ∩ F ) ∩ G = E ∩ (F ∩ G )
• Distributive laws: (E ∩ F ) ∪ G = (E ∪ G ) ∩ (F ∪ G );
(E ∪ F ) ∩ G = (E ∩ G ) ∪ (F ∩ G )
• DeMorgan’s laws: For events E1 , E2 , . . . , En ,
n
[
Ei
c
=
i=1
n
\
i=1
Ei
c
=
n
\
i=1
n
[
Eic
Eic
i=1
7
Axioms of Probability
Consider an experiment with sample space S.
Assume that, for each event E ⊂ S, a number P(E ) is defined and satisfies
the following three axioms:
Axiom 1:
0 ≤ P(E ) ≤ 1
Axiom 2:
P(S) = 1
Axiom 3: For any sequence of mutually exclusive events E1 , E2 , . . .
(i.e., Ei ∩ Ej = ∅ for all i 6= j)
P
∞
[
∞
X
Ei =
P(Ei )
i=1
i=1
8
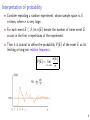
Interpretation of probability
• Consider repeating a random experiment, whose sample space is S,
n times, where n is very large.
• For each event E ⊂ S, let n(E ) denote the number of times event E
occurs in the first n repetitions of the experiment.
• Then it is natural to define the probability P(E ) of the event E as its
limiting or long-run relative frequency:
P(E ) = lim
n→∞
n(E )
n
9
Remarks:
• The long-run relative frequency interpretation of probability is referred
to as the frequentist approach
• Using this interpretation as the definition of probability is problematic
D Why should the limit exist? And if so, how to guarantee that the same
limit will be obtained for another sequence of repetitions of the
experiment?
D Postulating existence of the limit is a rather complicated assumption to
make
D Additionally, it is not always intuitive to interpret probability as a relative
frequency. For example, what is a probability that another earthquake
will occur in British Columbia tomorrow? Probability may represent a
person’s belief and thus be subjective (Bayesian view).
• The axiomatic approach to defining probability works regardless of the
interpretation of probability above you choose
10
Probability rules
1. Complement rule: P(E c ) = 1 − P(E )
2. If E ⊂ F , then P(E ) ≤ P(F )
3. General addition rule: P(E ∪ F ) = P(E ) + P(F ) − P(E ∩ F )
Addition rule: If E , F are mutually exclusive, then E ∩ F = φ and
P(E ∪ F ) = P(E ) + P(F )
11
Probability rules (cont’d)
4.
P
n
[
i=1
n
X
Ei =
P(Ei ) −
X
P(Ei1 ∩ Ei2 ) + · · ·
1≤i1 <i2 ≤n
i=1
X
+ (−1)r +1
P(Ei1 ∩ Ei2 ∩ · · · ∩ Eir ) + · · ·
1≤i1 <i2 <...<ir ≤n
+ (−1)n+1 P(E1 ∩ E2 ∩ · · · ∩ En )
Note: For the term
X
P(Ei1 ∩ Ei2 ∩ · · · ∩ Eir ), the
1≤i1 <i2 <...<ir ≤n
summation is taken over all the n Cr possible subsets of size r from the
set {1,2, ..., n}
12
For example, in order to find the probability of the union of three events,
we will apply the above formula:
P(E1 ∪ E2 ∪ E3 ) = P(E1 ) + P(E2 ) + P(E3 )
−P(E1 ∩ E2 ) − P(E1 ∩ E3 ) − P(E2 ∩ E3 )
[3 C2 subsets of size 2 from 3 events]
+P(E1 ∩ E2 ∩ E3 )
13
Probability rules (cont’d)
5. If all outcomes in S are equally likely, then
P(E ) =
Number of outcomes in E
Number of outcomes in S
14
Exercises
1. Five drivers are driving past a certain intersection. Two of them are
drunk and the others are sober. A police officer at the intersection
randomly stops two of the five cars for inspection.
(a) Write down the sample space for this random experiment (selection of
drivers by the police officer). How many possible selections are there?
Define notation:
Di = the ith drunk driver is selected
Ni = the ith sober driver is selected
15
(b) Find the probability that exactly one of the drunk drivers is selected.
16
2. In a college, 65% of the students own a car, 82% own a computer, and
55% own both. A student is randomly chosen. What is the probability
that the chosen student owns neither a car nor a computer?
Define events:
17
3. Three different orders are to be mailed to three suppliers. However, an
absent-minded secretary gets the orders mixed up, and sends them
randomly to the suppliers. If a match refers to the fact that a supplier
receives the correct order, find the probability of the following events.
(a) No matches occur.
(b) Exactly one match occurs.
18
4. A closet contains 10 pairs of shoes. If 8 shoes are randomly selected,
what is the probability that there will be
(a) no complete pair?
(b) exactly one complete pair?
19
5. There are k students in a class. What is the probability that at least
2 students have the same birthday?
(Assume that there 365 days a year and the probability of being born
on a given day is 1/365.)
If there are only two students in the class, what is the value of the
above probability?
20
Chapter 2 - Learning outcomes
Aim: Demonstrate an understanding of basic probability concepts
• Recognize the random experiment of interest in a given scenario
• List all possible outcomes in the sample space of a random experiment
• Appreciate the definitions of an event, the complement of an event,
unions and intersections of events
• Appreciate the meaning of a null set, and that of an event being
contained in another event
• Use Venn Diagrams to depict single events, complementary events,
unions and intersections of a collection of events
• Explain whether a collection of events are mutually exclusive
21
Chapter 2 - Learning outcomes (cont’d)
• Apply the Commutative, Associative, Distributive and DeMorgans laws
to unions and intersections of events
• Appreciate the probability of an event is a long-run relative frequency
of occurrences of the event in repetitions of a random experiment
• Recall the axioms of probability of an event
• Define appropriate events in solving probability problems
• Recognize if outcomes in a sample space are equally likely
• Determine the probability of an event where the outcomes in a sample
space are equally likely
• Apply probability rules (complement rule, addition/general addition rule
and others) in solving probability problems
22