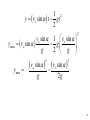Download Calculus 10.4

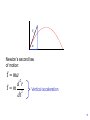
10.4 Projectile Motion
Fort Pulaski, GA
Photo by Vickie Kelly, 2002
Greg Kelly, Hanford High School, Richland, Washington
One early use of calculus was to study projectile motion.
In this section we assume ideal projectile motion:
Constant force of gravity in a downward direction
Flat surface
No air resistance (usually)

vo

We assume that the projectile is launched from the origin
at time t =0 with initial velocity vo.
Let vo  vo
then vo   vo cos  i   vo sin   j
The initial position is:
ro  0i  0 j  0

vo

Newton’s second law
of motion:
f  ma
2
d r
f m 2
dt
Vertical acceleration

vo

Newton’s second law
of motion:
f  ma
2
d r
f m 2
dt
The force of gravity is:
f  mg j
Force is in the downward direction

vo

Newton’s second law
of motion:
f  ma
2
d r
f m 2
dt
The force of gravity is:
f  mg j
2
d r
m 2  mg j
dt

vo

Newton’s second law
of motion:
f  ma
2
d r
f m 2
dt
The force of gravity is:
f  mg j
2
d r
m 2  mg j
dt

2
d r
 g j
2
dt
Initial conditions: r  ro
dr
 vo
dt
when t  o
dr
  gt j  v o
dt
1 2
r   gt j  vot  ro
2
1 2
r   gt j   vo cos  t i   vo sin   t j 0
2

1 2
r   gt j   vo cos   t i   vo sin   t j  0
2
Vector equation for ideal projectile motion:
1 2

r   vo cos   t i    vo sin   t  gt  j
2


1 2
r   gt j   vo cos   t i   vo sin   t j  0
2
Vector equation for ideal projectile motion:
1 2

r   vo cos   t i    vo sin   t  gt  j
2


Parametric equations for ideal projectile motion:
x   vo cos   t
1 2
y   vo sin   t  gt
2

Example 1:
A projectile is fired at 60o and 500 m/sec.
Where will it be 10 seconds later?
x  500  cos6010
x  2500
1
y  500sin 60 10   9.8 102
2
y  3840.13
The projectile will be 2.5 kilometers downrange and
at an altitude of 3.84 kilometers.
Note: The speed of sound is 331.29 meters/sec
Or 741.1 miles/hr at sea level.

The maximum height of a projectile occurs when
the vertical velocity equals zero.
dy
 vo sin   gt  0
dt
vo sin   gt
vo sin 
t
g
time at maximum height

The maximum height of a projectile occurs when
the vertical velocity equals zero.
dy
 vo sin   gt  0
dt
vo sin   gt
vo sin 
t
g
We can substitute this expression into the formula
for height to get the maximum height.

1 2
y   vo sin   t  gt
2
ymax
vo sin  1  vo sin  
  vo sin  
 g

g
2  g 
ymax 
 vo sin  
g
2
vo sin  


2
2
2g

1 2
y   vo sin   t  gt
2
ymax
vo sin  1  vo sin  
  vo sin  
 g

g
2  g 
2  vo sin    vo sin  


2g
2g
2
ymax
ymax
vo sin  


2g
2
2
2
maximum
height

When the height is zero:
time at launch:
1 2
0   vo sin   t  gt
2
1 

0  t  vo sin   gt 
2 

t 0

When the height is zero:
time at launch:
t 0
1 2
0   vo sin   t  gt
2
1 

0  t  vo sin   gt 
2 

1
vo sin   gt  0
2
1
vo sin   gt
2
time at impact
(flight time)
2vo sin 
t
g

If we take the expression for flight time and substitute
it into the equation for x, we can find the range.
x  vo cos  t
2vo sin 
x  vo cos  
g
If we take the expression for flight time and substitute
it into the equation for x, we can find the range.
x  vo cos  t
2vo sin 
x  vo cos  
g
2
vo
x
 2cos  sin  
g
2
vo
x
sin  2 
g
Range

The range is maximum when
sin  2 
is maximum.
sin  2   1
2  90o
  45
o
Range is maximum
when the launch
angle is 45o.
2
vo
x
sin  2 
g
Range

If we start with the parametric equations for projectile
motion, we can eliminate t to get y as a function of x.
x   vo cos  t
x
t
vo cos 
1 2
y   vo sin   t  gt
2
If we start with the parametric equations for projectile
motion, we can eliminate t to get y as a function of x.
x   vo cos  t
1 2
y   vo sin   t  gt
2
x
x
1 
x 
 t y   vo sin  
 g

vo cos 
vo cos  2  vo cos  
2
This simplifies to:

 2
g
y   2
 x   tan   x
2
 2vo cos  
which is the equation of a parabola.

If we start somewhere besides the origin, the equations
become:
x  xo   vo cos  t
1 2
y  yo   vo sin   t  gt
2

Example 4:
A baseball is hit from 3 feet above the ground with an
initial velocity of 152 ft/sec at an angle of 20o from the
horizontal. A gust of wind adds a component of -8.8 ft/sec
in the horizontal direction to the initial velocity.
The parametric equations become:
x  152 cos 20  8.8  t
o
vo

y  3  152sin 20o  t  16t 2
yo
1
g
2

These equations can be graphed on the TI-89 to model
the path of the ball:
t2
Note that the calculator is in degrees.


Using
the
trace
function:
Max height about 45 ft
Time
about
3.3 sec
Distance traveled about 442 ft

In real life, there are other forces on the object. The
most obvious is air resistance.
If the drag due to air resistance is proportional to
the velocity:
(Drag is in the opposite
Fdrag  kv
direction as velocity.)
Equations for the motion of a projectile with linear drag
force are given on page 546.
You are not responsible for memorizing these formulas.
p