Download Device Modeling - Dr. Imtiaz Hussain

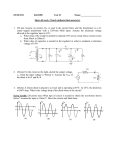
Modeling & Simulation of
Semiconductor Devices
LECTURE#5-6
Basics of Device Modeling Approaches
Course: ME-ESE-11
By: Engr. Irfan Ahmed Halepoto
Device Modeling





It is extremely important to have a valid device modeling &
simulation design prior to the device fabrication b/c technology &
design iteration are expensive and post fabrication tuning is not a
fun.
Modern device designing is very complex, so it is difficult to predict
performance characteristics of device without accurate computer
models
Device modeling actually describes the principal methods of
representing and analyzing devices (modern solid-state) .
Device modeling is useful in device design, production control and
performance analysis.
The utmost purpose of any device modeling is to
 Cuts Cost (economical)
 Cuts development time (faster manufacturing)
 Accurate designing
 “cutting edge” concept (reduced size).
 Minimize system complexities
Device Modelling Classification



Diode device Modeling
Transistor device Modeling
Semiconductor device Modeling (ICs)
Diode device Modeling


Diode Modeling: refers to the mathematical models used to approximate
the actual behavior of real diodes to enable calculations and circuit
analysis.
 diode's V-I curve is nonlinear (described by the Shockley diode law).
 This nonlinearity complicates calculations in circuits involving diodes,
so simpler models are often required.
Diode Modeling may be categorized as
 Large signal diode modeling (Non-linear): deals with any ACTIVE
components.
 Shockley diode model
 Diode-resistor model
 Large signal diode modeling is based on either
 Graphical modeling method
 Piecewise linear (PWL) modeling
 Mathematically idealized diode Modeling
 small signal diode modeling (Linear): deals with any PASSIVE
components.
 Resistance, Capacitance.
Graphical modeling method





Graphical analysis is a simple way to
derive a numerical solution to the
transcendental equations describing the
diode.
As with most graphical methods, it has
the advantage of easy visualization.
By plotting the V-I curves, it is possible
to obtain an approximate solution to
any arbitrary degree of accuracy.
This method plots the two currentvoltage equations on a graph and the
point of intersection of the two curves
satisfies both equations, giving the
value of the current flowing through the
circuit and the voltage across the diode.
Graphical method is often time
consuming and is impractical for
complex circuits .
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients
are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation.
Piecewise linear modeling







Piecewise linear (PWL) modeling takes a
function f(t) and breaks it into several linear
segments.
The graph shows how a curve can be
approximated by three linear segments,
forming a three-segment PWL model.
PWL method is used to approximate the diode
characteristic curve into linear segments.
This enables us to substitute the real diode for
an ideal diode, a voltage source and a resistor.
The figure shows a real diode V-I curve being
approximated by a two segment PWL model.
Typically the sloped line segment would be
chosen tangent to the diode curve at the Qpoint.
Then the slope of this line is given by the
reciprocal of the small-signal resistance of the
diode at the Q-point.
piecewise linear approximation of a curve
A piecewise linear approximation of the diode characteristic.
Mathematically idealized diode




Let us consider a mathematically idealized
diode.
In such an ideal diode, if the diode is
reverse biased, the current flowing through
it is zero.
This ideal diode starts conducting at 0 V
and for any positive voltage an infinite
current flows and the diode acts like a short
circuit.
The I-V characteristics of an ideal diode
are shown.
I-V characteristic of an ideal diode
Ideal diode in series with voltage source






Consider the case when we add a voltage
source in series with the diode as shown .
When forward biased, ideal diode is simply
a short circuit and when reverse biased, an
open circuit.
If the anode of the diode is connected to
0 V, voltage at the cathode will be at Vt
and the potential at the cathode will be
greater than the potential at the anode
and the diode will be reverse biased.
In order to get the diode to conduct,
voltage at the anode will need to be
taken to Vt.
This circuit approximates the cut-in
voltage present in real diodes.
The combined I-V characteristic of this
circuit is shown .
Ideal diode with a series voltage source
I-V characteristic of and ideal diode with a series voltage source
Diode with voltage source & current-limiting resistor



The last thing needed is a resistor
to limit the current, as shown with
the I-V characteristic.
The real diode now can be
replaced with the combined ideal
diode, voltage source and resistor
and the circuit then is modeled
using just linear elements.
If the sloped-line segment is
tangent to the real diode curve at
the Q-point, this approximate
circuit has the same small-signal
circuit at the Q-point as the real
diode.
Ideal diode with a series voltage source
and resistor
I-V characteristic of an ideal diode with a series voltage source and resistor
Transistor device Modeling




Transistors are simple devices with complicated behavior.
In order to ensure the reliable operation of circuits
employing transistors, it is necessary to scientifically model
the physical phenomena observed in their operation using
transistor models.
There exists a variety of different models that range in
complexity and in purpose.
Transistor models divide into two major groups:
 Models for device design
 Models for circuit design
Models for device design





Modern transistor has an internal structure that exploits complex
physical mechanisms.
Device design requires a detailed understanding of how device
manufacturing processes carried like Ion implantation, Impurity
diffusion, Oxide growth, Annealing, Etching affect device behavior.
Process models simulate the manufacturing steps and provide a
microscopic description of device "geometry" to the device
simulator.
By "geometry" is meant not only readily identified geometrical
features such as whether the gate is planar or wrap-around, or
whether the source and drain is altered or not but also details
inside the structure, such as the doping profiles after completion of
device processing.
Physical processes in the device determine its electrical behavior
in a variety of circumstances:
 DC current-voltage behavior,
 transient behavior (both large-signal and small-signal),
 Internal variation in device response.
Models for circuit design (compact models)





Transistor models are used for almost all modern electronic design work.
Analog circuit simulators such as SPICE (Simulation Program with
Integrated Circuit Emphasis) use models to predict the behavior of a
design.
LT SPICE is getting popularity too.
Most design work is related to IC designs which have a very large tool
cost, primarily for the photo masks used to create the devices, and there
is a large economic incentive to get the design working without any
iterations.
Device models must include effect of various parameters on design like:
 Width & length
 Interdigitation
 Proximity to other devices
 Transient and DC current-voltage characteristics
 Parasitic device capacitance
 Resistance and inductance
 Time delays
 Temperature effects
Transistor – Large signal nonlinear models

Large signal transistor models (non-linear models) fall into
three main types.
 Physical models
 Empirical models
 Tabular models
Physical models


These are models based upon device physics, which relies on the
approximate modeling of physical phenomena within a transistor.
Parameters within these models are based upon physical
properties such as
 Oxide thicknesses, Substrate doping concentrations, Carrier
mobility, etc.
Empirical models



Empirical models are based upon curve fitting, subjected to the parameter
and values which can fit describe the operation of the device (transistor).
Unlike a physical model, empirical model parameters are not based
fundamentals, they mostly depends on the fitting procedure used to find
them.
Fitting procedure is key to success of these models if they are to be used
to extrapolate to designs lying outside the range of data to which the
models were originally fitted.
Empirical model of carrier scattering
on ionized impurity
Tabular models




Tabular models are based on lookup table (LUT) form, by considering
effect of one parameter to the other.
 Effect of parasitic components on
drain current
These values are indexed in
reference to their corresponding
bias voltage combinations.
Thus, model accuracy is increased
by inclusion of additional data
points within the table.
Limitation of these models is that
they work best for designs that use
devices
within
the
table
(interpolation) and are unreliable for
devices
outside
the
table
(extrapolation).
Transistor – Small-signal linear models





Small-signal or linear models are used to evaluate stability,
gain, noise and bandwidth.
A small-signal model is generated by taking derivatives of the
current-voltage curves about a bias point or Q-point.
As long as the signal is small relative to the nonlinearity of
the device, the derivatives do not vary significantly, and can
be treated as standard linear circuit elements.
Advantage of small signal models is that they can be solved
directly, while large signal nonlinear models are generally
solved iteratively, with possible convergence or stability
issues.
By simplification to a linear model, the whole apparatus for
solving linear equations becomes available, for example,
simultaneous equations, determinants, and matrix theory etc.
Small-signal parameters






A transistor’s parameters represent its electrical properties.
Engineers employ transistor parameters in production-line testing and
in circuit design.
A group of a transistor’s parameters sufficient to predict circuit gain,
input impedance, and output impedance are components in its smallsignal model.
Parameters used in small-signal circuits (two ports) adopt names
related to the names of these circuits such as
 Transmission parameters (T-parameters),
 Hybrid-parameters (h-parameters),
 Impedance parameters (z-parameters),
 Admittance parameters (y-parameters), and
 Scattering parameters (S-parameters).
These parameters all can be evaluated using measured scattering
parameter data.
Scattering parameters (S parameters) can be measured for a
transistor at a given bias point with a vector network analyzer.
Semiconductor device modeling

Semiconductor device modeling creates models for the behavior of
the electrical devices based on fundamental physics, such as the
doping profiles of the devices.
 The intent of IC fabrication is to produce a wafer with specific
electrical & mechanical characteristics, usually in the form of
electronic circuits or chips, via some number of processing
transformations.
Why need semiconductor modeling?



semiconductor modeling is based on a computational
modeling mechanism, which is the evaluation & optimization
of various design, without resorting to costly and timeconsuming trial fabrication and measurement steps.
It may also include the creation of compact models (such as
the SPICE (Simulation Program with Integrated Circuit
Emphasis) transistor models, which try to capture the
electrical behavior of such devices but do not generally
derive them from the underlying physics.
 Provides valuable insight into important physical quantities.
 Shortened development cycles.
 Reduced cost.
 Increased quality and reliability of final products.
A important field of computational modeling related to
semiconductor manufacturing belongs to process modeling.
Semiconductor device models



Semiconductor device models can be considered in two
broad categories
 Physical device models
 Equivalent circuit models.
Physical device models: attempt to incorporate the physics
of device operation.
Equivalent circuit models: are based on electrical circuit
analogies representing the electrical behavior.
Physical device models



Physical device models can provide greater insight into the
detailed operation and operating conditions of semiconductor
devices, but usually based on a lengthy analysis.
 Dependent
on numerical techniques implemented on
computers.
Physical device models are solved using either bulk carrier
transport equations (the semiconductor equations), solutions to
the Boltzmann transport equation or quantum transport
concepts.
 Bulk transport solutions have satisfied most device models
 Boltzmann and quantum transport solutions have provided a
strong insight into the detailed device physics.
The understanding of material properties, physical boundary
conditions (such as surface physics, contact properties and
device geometry) and device-circuit interaction are steadily
improving, allowing more intricate models to be developed.
Physical device models
Equivalent circuit models


Equivalent circuit models approach is generally limited in its
applicability because of the DC bias, frequency dependence
and the non-linear behavior of most devices with respect to
signal level.
The principal advantage of this technique is that it is easy to
implement and analyze.
Equivalent circuit models
BJT Equivalent Circuit th rough diode
Equivalent Circuit Model: NPN BJT Small signal