* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 5 Triangles and the Pythagorean Theorem Notes
Rotation formalisms in three dimensions wikipedia , lookup
Rule of marteloio wikipedia , lookup
Line (geometry) wikipedia , lookup
History of trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Multilateration wikipedia , lookup
Integer triangle wikipedia , lookup
Rational trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
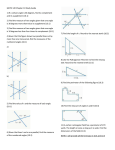
1. 2. Go to the “Brain Pop” app and search watch the “Angles” video. (If you don’t have earbuds, watch with captions) Take the quiz. It will record your results. Symbols Define it in your own words Draw it Describe a realworld example of it Parallel Perpendicular ∥ ⊥ Interior angles: ∠3, ∠4, ∠5, ∠6 Exterior angles: ∠1, ∠2, ∠7, ∠8 Alternate Interior angles: 𝑚∠4 = 𝑚∠6, 𝑚∠3 = 𝑚∠5 Alternate Exterior angles: 𝑚∠1 = 𝑚∠7 𝑚∠2 = 𝑚∠8 Corresponding angles: 𝑚∠1 = 𝑚∠5, 𝑚∠2 = 𝑚∠6 Classify each pair of angles in the figure as alternate interior, alternate exterior, or corresponding. a. ∠1 𝑎𝑛𝑑 ∠7 alternate exterior angles b. ∠2 𝑎𝑛𝑑 ∠6 corresponding angles Classify the relationship between ∠4 and ∠6 If m∠1 = 50˚, find m∠2, m∠3, and m∠4. m∠2 = 130˚ because ∠1 and ∠2 are supplementary. m∠4 = 130˚ because ∠1 and ∠4 are supplementary. m∠3 = 50˚ because ∠1 and ∠3 are vertical angles. A furniture designer built the bookcase shown. Line a is parallel to line b. If m∠2 = 105˚, find m∠6 and m∠3. Justify your answer. Since ∠2 and ∠6 are supplementary, the m∠6 = 75˚. Since ∠6 and ∠3 are interior angles, so the m∠3 is 75˚. Find the measure of angle 4. In the figure, line m is parallel to line n, and line q is perpendicular to line p. The measure of ∠1 is 40˚. What is the measure of ∠7. Since ∠1 and ∠6 are alternate exterior angles, m∠6 = 40˚. Since ∠6, ∠7, and ∠8 form a straight line, the sum is 180˚. 40 + 90 + m∠7 = 180 So m∠7 is 50˚. Every time Bill watches his favorite team on TV, the team loses. So, he decides to not watch the team play on TV. In order to play sports, you need to have a B average. Simon has a B average, so he concludes that he can play sports. All triangles have 3 sides and 3 angles. Mariah has a figure with 3 sides and 3 angles so it must be a triangle. After performing a science experiment, LaDell concluded that only 80% of tomato seeds would grow into plants. Deductive Reasoning Inductive Reasoning STEP 1: List the given information, or what you know. Draw a diagram if needed. STEP 2: State what is to be proven. STEP 3: Create a deductive argument by forming a logical chain of statements linking the given information. STEP 4: Justify each statement with definitions, properties, and theorems STEP 5: State what it is you have proven. A proof is a logical argument where each statement is justified by a reason. A paragraph proof or informal proof involves writing a paragraph. A two-column proof or formal proof contains statements and reason organized in two columns. Once a statement has been proven, it is a theorem. The diamondback rattlesnake has a diamond pattern on its back. An enlargement of the skin is shown. If m∠1 = m∠4, write a paragraph proof to show that m∠2 = m∠3. Given: m∠1 = m∠4 Prove: m∠2 = m∠3 Proof: m∠1 = m∠2 because they are vertical angles. Since m∠1 = m∠4, and m∠2 = m∠4. The measure of angle 3 and 4 are the same since they are vertical angles. Therefore, m∠2 = m∠3. Refer to the diagram shown. AR = CR and DR = BR. Write a paragraph proof to show that AR + DR = CR + BR. Given: AR = ___________ and DR = ____________. Prove: _________________ = CR + BR. Proof: You know that AR = CR and DR = BR. AR + DR = CR + BR by the _____________ Property of Equality. So, AR + DR = CR + BR by ___________________. Write a two-column proof to show that if two angles are vertical angles, then they have the same measure. Given: lines m and n intersect; ∠1 and ∠3 are vertical. Prove: m∠1 = m∠3 Statements Reasons a. Lines m and n intersect; Given ∠1 and ∠3 are vertical. b. ∠1 and ∠2 are a linear Definition of linear pair pair and ∠3 and ∠2 are a linear pair. c. m ∠1 and m∠2 = 180˚ Definition of supplemental m∠3 and m∠2 = 180˚ angles d. m ∠1 and m∠2 = m∠3 and m∠2 Substitution e. m∠1 = m∠3 Subtraction Property of Equality The statements for a two-column proof to show that if m∠Y = m∠Z, then x =100 are given below. Complete the proof by providing the reasons. Statements a. m ∠Y = m∠Z, m ∠Y = 2x – 90 m∠Z = x + 10 b. 2x – 90 = x + 10 c. x – 90 = 10 d. x = 100 Reasons Given 1. What is true about the measures of ∠1 and ∠2? Explain. 2. What is true about the measures of ∠3 and ∠4? 3. What kind of angle is formed by ∠1, ∠5, and ∠3? Write an equation representing the relationship between the 3 angles. 4. Draw a conclusion about ΔABC. Words: The sum of the measures of the interior angles of a triangle is 180˚. Symbols: Model: x + y + z = 180˚. Find the value of x in the Antigua and Barbuda flag. x + 55 + 90 = 180 x + 145 = 180 x = 35 The value of x is 35. In ΔXYZ, if m∠X = 72˚ and m∠Y = 74˚, what is m∠Z? The measures of the angles of ΔABC are in the ratio 1:4:5. What are the measures of the angles? Let x represent angle A, 4x angle B, and 5x angle C x + 4x + 5x = 180 10x = 180 x = 18 Angle A = 18˚ Angle B = 18(4) = 72˚ Angle C = 18(5) = 90˚ The measures of the angles of ΔLMN are in the ratio 2:4:6. What are the measures of the angles? Words: The measure of an exterior angle is equal to the sum of the measures of its two remote interior angles. Symbols: Model: m∠A + m∠B = m∠1 Each exterior angle of the triangle has two remote interior angles that are not adjacent to the exterior angle. 4 1 interior exterior 3 5 2 6 ∠4 is an exterior angle. It’s two remote angles are ∠2 and ∠3. m∠4 = m∠2 + m∠3 Suppose m∠4 = 135˚. Find the measure of ∠2. First Way: Angle 4 is the exterior angle with angle 2 and angle K as the remote interior. Second Way: ∠4 and ∠ 1 are supplementary, so they equal 180˚. ∠ 4 + ∠ 1 = 180 135 + ∠ 1 = 180 ∠ 1 = 45 ∠2 + ∠K = ∠ 4 ∠ 2 + 90 = 135 ∠ 2 = 45˚ ∠ 1 + ∠ 2 + ∠ K = 180 45 + ∠ 2 + 90 = 180 ∠ 2 = 45˚ Suppose m ∠ 5 = 147˚. Find m ∠ 1. A polygon is a closed figure with three of more line segments. List the states that are in a shape of a polygon. Words: The sum of the measures of the interior angles of a polygon is (n – 2)180, where n is the number of sides. Symbols: S = (n – 2)180 Regular Polygons – an equilateral (all sides are the same) and a equiangular (all angles are the same) Find the sum of the measures of the interior angles of a decagon. S = (n -2)180 S = (10 – 2)180 S = (8)180 S = 1,440 The sum of the interior angles of a 10-sided polygon is 1,440˚. Find the sum of the measures of the interior angles of each polygon. a. Hexagon b. Octagon c. 15-gon Each chamber of a bee honeycomb is a regular hexagon. Find the measure of an interior angle of a regular hexagon. STEP 1: Find the sum of the measures of angle. S = (n – 2)180 S = (6 – 2)180 S = (4)180 S = 720˚ STEP 2: Divide 720 by 6, since there are six angles in a hexagon. 720˚÷ 6 = 120 Each angle in a hexagon is 120˚ Find the measure of one interior angle in each regular polygon. Round to the nearest tenth if necessary. a. octagon b. heptagon c. 20-gon Words: The sum of the measures of the exterior angles, one at each vertex, is 360˚. Symbols: m∠1 + m ∠ 2 + m ∠ 3 + m ∠ 4 + m ∠ 5 = 360˚ Model: Examples: Find the measure of an exterior angle in a regular hexagon. A hexagon has a 6 exterior angles. 6x = 360 x = 60 Each exterior angle is 60˚. Find the measure of an exterior angle in a regular polygon. a. triangle b. quadrilateral c. octagon Words: In a right triangle, the sum of the squares of the legs equal the square of the hypotenuse. Symbols: a2 + b2 = c2 Model: c a b Find the missing length. Round to the nearest tenth. c 12 in 9 in a2 + b2 = c2 92 + 122 = c2 81 + 144 = c2 225 = c2 ± 𝟐𝟐𝟓 = c c = 15 and -15 The equation has two solutions, -15 and 15. However, the length of the side must be positive. The hypotenuse is 15 inches long. Find the missing length. Round to the nearest tenth. b 24 cm 8 cm a2 + b2 = c2 82 + b2 = 242 64 + b2 = 576 64 – 64 + b2 = 576 - 64 b2 = 512 b = ± 𝟓𝟏𝟐 b ≈ 22.6 or -22.6 The length of leg b is 22.6 cm long. Find the missing length. Round to the nearest tenth if necessary. a. b. STATEMENT: If a triangle is a right triangle, then a2 + b2 = c2. CONVERSE: If a2 + b2 = c2, then a triangle is a right triangle. The converse of the Pythagorean Theorem is also true. The measures of three sides of a triangle are 5 inches,12 inches and 13 inches. Determine whether the triangle is a right triangle. a2 + b2 = c2 52 + 122 = 132 25 + 144 = 169 169 = 169 The triangle is a right triangle. Determine if these side lengths makes a right triangle. a. 36 in, 48 in, 60 in b. 4 ft, 7ft, 5ft Write an equation that can be used to find the length of the ladder. Then solve. Round to the nearest tenth. a2 + b2 = c2 8.752 + 182 = x2 76.5625 + 324 = x2 400.5625 = x2 ± 𝟒𝟎𝟎. 𝟓𝟔𝟐𝟓 = x 20.0 ≈ x The ladder is about 20 feet. Write an equation that can be used to find the length of the ladder. Then solve. Round to the nearest tenth. a2 + b2 = c2 102 + b2 = 122 100 + b2 = 144 b2 = 44 b = ± 𝟒𝟒 b ≈ 6.6 The height of the plane is about 6.6 miles. Mr. Parsons wants to build a new banister for the staircase shown. If the rise of the stairs of a building is 5 feet and the run is 12 feet, what will be the length of the new banister? A 12-foot flagpole is placed in the center of a square area. To stabilize the pole, a wire will stretch from the top of the pole to each corner of the square. The flagpole is 7 feet from each corner of the square. what is the length of each wire. Round to the nearest tenth. a2 + b2 = c2 72 + 122 = c2 49 + 144 = c2 193 = c2 ± 𝟏𝟗𝟑 = c2 13.9 ≈ c The length of the wire is about 13.9 feet. The top part of a circus tent is in the shape of a cone. The tent has a radius of 50 feet. The distance from the top of the tent to the edge is 61 feet. How tall is the top part of the tent? Round to the nearest whole number. Graph the ordered pairs (3, 0) and (7, 5). Then find the distance c between the two points. Round to the nearest tenth. a2 + b 2 = c2 5 2 + 4 2 = c2 25 + 16 = c2 41 = c2 ± 𝟒𝟏 = c2 6.4 ≈ c The points are about 6.4 units apart. Graph the ordered pairs (1, 3) and (-2, 4). Then find the distance c between the two points. Round to the nearest tenth. Symbols: The distance d between two points with coordinates (x1, y1) and (x2, y2) is given by the formula d= Model: 𝑥2 − 𝑥1 2 + 𝑦2 − 𝑦1 2 On the map, each unit represents 45 miles. West Point, New York is located at (1.5, 2) and Annapolis, Maryland, is located at (-1.5, -1.5). What is the approximate distance between West Point and Annapolis? METHOD 1: Use the Pythagorean Theorem a2 + b2 = c2 32 + 3.52 = c2 21.25 = c2 ± 𝟐𝟏. 𝟐𝟓 = c ± 4.6 ≈ c Since the map units equals 45 miles, the distance between the cities is 4.6(45) or about 207 miles. On the map, each unit represents 45 miles. West Point, New York is located at (1.5, 2) and Annapolis, Maryland, is located at (-1.5, -1.5). What is the approximate distance between West Point and Annapolis? METHOD 2: Use the Distance Formula c = 𝑥2 − 𝑥1 2 + 𝑦2 − 𝑦1 2 c= −1.5 − 1.5 c= −3 2 2 + −1.5 − 2 + −3.5 c = 9 + 12.25 c = 21.25 ≈ ± 4.6 2 2 Since the map units equals 45 miles, the distance between the cities is 4.6(45) or about 207 miles. Cromwell Field is located at (2.5, 3.5) and Deadwoods Field is at (1.5, 4.5) on a map. If each map unit is 0.1 mile, about how far apart are the fields? Use the Distance Formula to find the distance between X(5, -4) and Y(-3, -2). Round to the nearest tenth if necessary. d= 𝟓 − (−𝟑 𝟐 + −𝟒 − (−𝟐 𝟐 d = 𝟖𝟐 + 𝟐𝟐 d = 𝟔𝟒 + 𝟒 d = 𝟔𝟖 d ≈ ± 8.2 This distance between the points is about 8.2 units.