Download Area of Polygons and Circles

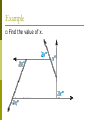
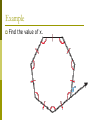
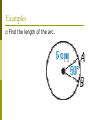
Area of Polygons and
Circles
Chapter 11
11.1 Angle Measures in Polygons
The sum of the measures of the interior
angles of a polygon depends on the
number of sides.
 Determining how many triangles are in
each polygon will help you figure out the
sum of the measures of the interior
angles.

Sum of interior angles

Draw all the diagonals from one vertex.
This will divide the polygon into triangles.
Polygon Interior Angle Theorem

The sum of the measures of the interior
angles of a convex n-gon is (n-2)*180 .

The measure of each interior angle of a
regular n-gon is (n  2)  180
n
Examples

Find the value of x.
Polygon Exterior Angle Theorem

The sum of the measures of the exterior
angles of a convex polygon, one angle at
each vertex, is 360 .

The measure of each exterior angle of a
regular n-gon is 360
n
Example

Find the value of x.
Example

Find the value of x.
11.2 Areas of Regular Polygons
Regular Polygon: all sides are same
length
 You know that the area of a triangle is
equal to A = ½ bh.
 If you are dealing with an equilateral
triangle there is a special formula:
1 2
A =
s 3
4


(s = side)
Example

Find the area of an equilateral triangle
with 8-inch sides.
Vocabulary

When dealing with a polygon, think of it as
if it were inscribed in a circle:
Vocabulary
Center of a polygon: the same as the
center of the circumscribed circle
 Radius of the polygon: the same as the
radius of the circumscribed circle



G is the center of the polygon
GA is the radius F
A
G
E
D
B
C
Vocabulary

Apothem of the polygon: the distance
from the center to any side of the
polygon.

The apothem is the segment GH.
F
A
H
G
E
D
B
C
Area of a Regular Polygon

The area of a regular n-gon with side
length s is half the product of the
apothem a and the perimeter P.
1
 A = aP
2
6
4
Central angle of a regular polygon
An angle whose vertex is the center and
whose sides contain two consecutive
vertices of the polygon.
 You can divide 360 by the number of
sides (n) to find the measure of each
central angle.

Examples

Find the area of the regular octagon.



P = __________
Apothem = ___________
Area = _____
8.3
4.3
11.3 Similar Figures

If two polygons are similar with the
lengths of corresponding sides in the ratio
of a:b, then the ratio of their areas is
a2:b2
Similar Figures

The ratio of the lengths of corresponding
sides is 1:2.


The ratio of the perimeters is also 1:2.
The ratio of the areas is 1:4.
11.4 Circumference and Arc Length

Circumference of a circle: the distance around
the circle.

Arc length: a portion of the circumference of a
circle.



Measure of an arc – degrees
Length of an arc – linear units
The circumference C of a circle is:


.C  d
.C  2r


d is the diameter of the circle
r is the radius of the circle
Arc Length Corollary

The ratio of the length of a given arc to
the circumference is equal to the ratio of
the measure of the arc to 360 .


Arc length of AB = mAB
2r
360
mAB
 2r
Arc length of AB =
360
A
P
B
Arc Lengths

The length of a semicircle = ½ of the
circumference.

The length of a 90 arc = ¼ of the
circumference.
Examples

Find the length of the arc.
Examples

Find the length of the arc.
Example

Find the circumference.
Examples

Find the measure of XY.
11.5 Areas of Circles and Sectors
r
2

Area of a Circle =

Find the area of the circle.
8 in.
Examples

Find the diameter of the circle if the area
is 96 cm2.
Z
Sector of a Circle

Sector of a Circle: the region bounded by
two radii of the circle and their intercepted
arc.
Area of a Sector

The ratio of the area, A, of a sector of a
circle to the area of the circle is equal to
the ratio of the measure of the intercepted
arc to 360 .
A mAB
 .

2
r
360
Examples

Find the area of the sector.
Examples

A and B are two points on the circle with
radius 9 inches and m APB = 60 . Find
the areas of each sector.
Finding areas of Regions
Area of
shaded =
region
Area of
circle
-
Area of
polygon
Examples

Find the area of the shaded region.
11.6 Geometric Probability

Probability is a number from 0 to 1 that
represents the chance that an event will
occur.

Geometric Probability is a probability that
involves a geometric measure such as
length or area.
Probability and Length

Let AB be a segment that contains the
segment CD. If a point K on AB is chosen
at random, then the probability that it is
on CD is:

P(Point K is on CD) = Length of CD
Length of AB
A
C
D
B
Probability and Area

Let J be a region that contains region M.
If a point K in J is chosen at random, then
the probability that it is in region M is:

P(Point K is in region M) = Area of M
Area of J
J
M
Examples

Find the probability that a point chosen at
random on RS is on TU.
R
1
2
T
3
4
5
6
U
7
8
S
9 10 11 12 13 14 15
Examples

Find the probability that a randomly
chosen point in the figure lies in the
shaded region.
Examples

Find the probability that a randomly
chosen point in the figure lies in the
shaded region.