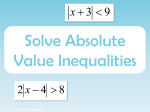* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Inequalities ≤ + 19
Survey
Document related concepts
Transcript
Inequalities
Inequalities:
“Some problems in algebra lead to inequalities instead of equations. An inequality looks just
like an equation, except that in the place of the equal sign is one of the symbols (<,>, ≤, ≥ )”.
Ex: 4 x + 7 ≤ 19
To solve an inequality that contains a variable means to find all values of the variable that
make the inequality true. Unlike an equation, an inequality generally has infinitely many solutions,
which form an interval or a union of intervals on the real line.
There is a difference between an equation and an inequality. It is illustrated with the following number
line.
x=3
Equation: 4 x + 7 = 19
Solution:
Inequality: 4 x + 7 ≤ 19
x≤3
Solving Linear Inequalities
-Linear inequalities involve one variable.
Ex.
x + 3 < 4 is a linear inequality.
-All of the rules that apply to equations also apply to inequalities with one
important exception.
If you ever multiply or divide by a negative number you must reverse
the direction of the inequality sign.
The Math Center
■
Valle Verde
■
Tutorial Support Services
■
EPCC
1
4 x − 6 > 2 x + 10
Example:
Solution:
Add 6 to both sides:
4 x − 6 + 6 > 2 x + 10 + 6
Subtract 2x from both sides:
4 x − 2 x > 2 x + 16 − 2 x
Divide both sides by 2:
2 x 16
>
2
2
Answer:
x > 8 or (8, ∞)
Interval Notation
Another method of representing inequalities is with interval notation.
Example:
)
[
3
x
5
This can be written as 3≤x<5 or [3, 5)
This is known as Interval Notation.
-From this notation you can see that there is a left boundary at 3 and a right boundary at 5.
-When you have a parenthesis or a greater than (>) or less than (< ) symbol the number is
not included in the set, but that does not mean that you cannot include numbers close to it
such as 4.1, 4.5, 4.9, and 4.999.
Solving Compound Inequalities
-Compound inequalities involve two inequalities of the same variable.
− 3 < 2x + 1 < 5
Example:
This one inequality can be written as two inequalities.
− 3 < 2x + 1
2x + 1 < 5
and
Each inequality is solved separately.
Note: Another method would be to apply properties of equations to all
parts of the inequalities.
The Math Center
■
Valle Verde
■
Tutorial Support Services
■
EPCC
2
Solving Absolute Value Inequalities
-Solving inequalities involving absolute values requires learning 2 new rules that will affect
how the problem is solved.
A. When solving an inequality in which the absolute value expression is less than (<) or less
than or equal to (≤) a standard expression, such as |x+3| ≤ 5, we must rewrite this as -5≤x+3≤5
and solve.
B. When solving an inequality in which the absolute value expression is greater than (>) or
greater than or equal to (≥) a standard expression, such as |2x-1|>7, we must rewrite this as
2x-1<-7 or 2x-1>7 and solve each inequality separately.
Properties of Absolute – Value Inequalities
Inequality
Equivalent form
−c < x < c
1. x < c
Graph:
2. x ≤ c
-c
c
−c ≤ x ≤ c
Graph:
-c
c
x < −c or
3. x > c
x
x>c
Graph:
x
-c
c
x ≤ −c or
4. x ≥ c
x≥c
x
Graph:
-c
Example:
c
|x+3| ≤ 5
Rewrite:
Subtract 3 from all parts:
−5≤ x+3≤ 5
−5−3 ≤ x +3−3 ≤ 5−3
−8 ≤ x ≤ 2
Simplify:
The Math Center
x
■
Valle Verde
or [-8, 2]
■
or {x|-8≤x≤2}
Tutorial Support Services
■
EPCC
3




![{ } ] (](http://s1.studyres.com/store/data/008467374_1-19a4b88811576ce8695653a04b45aba9-150x150.png)