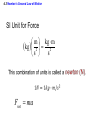* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Newton's Second Law of Motion
Survey
Document related concepts
Center of mass wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Coriolis force wikipedia , lookup
Classical mechanics wikipedia , lookup
Equations of motion wikipedia , lookup
Fundamental interaction wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Seismometer wikipedia , lookup
Fictitious force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Centrifugal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
Transcript
Chapter 4
Forces
and
Newton’s Laws of
Motion
4.1 The Concepts of Force and Mass
1) A force is a push or a pull.
Contact forces arise from physical
contact .
Action-at-a-distance forces do not
require contact and include gravity
and electrical forces.
4.1 The Concepts of Force and Mass
Arrows are used to represent forces. The length of the arrow
is proportional to the magnitude of the force.
15 N
5N
4.1 The Concepts of Force and Mass
2) Mass is a measure of the amount
of “stuff” contained in an object.
SI Unit of Mass: kilogram (kg)
Galileo vs. Aristotle
In our experience, objects must be pushed in order to keep
moving. So a force would be needed to have a constant
velocity. This is what Aristotle claimed in his in his series
of books entitled "Physics", written 2400 years ago.
But 400 years ago, another scientist and astronomer,
Galileo, proposed the following thought experiment which
revealed another perspective.
Thought Experiment
Imagine two perfectly smooth ramps connected
together by a perfectly smooth surface. If a ball is let
go at the top of the one ramp, what will happen?
Thought Experiment
Imagine two perfectly smooth ramps connected
together by a perfectly smooth surface. If a ball is let
go at the top of the one ramp, what will happen?
Thought Experiment
Imagine two perfectly smooth ramps connected
together by a perfectly smooth surface. If a ball is let
go at the top of the one ramp, what will happen?
Thought Experiment
Imagine two perfectly smooth ramps connected
together by a perfectly smooth surface. If a ball is let
go at the top of the one ramp, what will happen?
Thought Experiment
If a ball rolls down one ramp, it
keeps rolling up the other side
until it reaches the same height.
Thought Experiment
Now repeat that experiment, but make the second
ramp less steep.
What Will Happen?
Thought Experiment
Now repeat that experiment, but make the second
ramp less steep.
What Will Happen?
Thought Experiment
Now repeat that experiment, but make the second
ramp less steep.
What Will Happen?
Thought Experiment
Now repeat that experiment, but make the second
ramp less steep.
What Will Happen?
Thought Experiment
It will still keep rolling until it reaches the same
height, but it has to roll farther!
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
Finally, make the ramp flat.
Now what will happen?
Thought Experiment
It will keep rolling forever, no
external force is necessary.
Galileo vs. Aristotle
It's not that Aristotle was wrong.
In everyday life, objects do need to keep being pushed in order
to keep moving.
Push a book across the table. When you stop pushing, it stops
moving. Aristotle is right in terms of what we see around us
every day.
Force and Motion
It's just that Galileo, and later Newton,
imagined a world where friction could be
eliminated.
Friction represents an
external force acting on the
object, just as your push is
an external force.
Fapplied
Ffriction
In the absence of all external forces, an object's velocity
remains constant. Two equal and opposite forces have the
same effect, they cancel to create zero net force.
4.2 Newton's 1st Law of Motion
Sir Isaac Newton
Galileo's observations
were more fully formed
in 1687 by the 'father of
physics, ' Sir Isaac
Newton, who called this
observation "The First
Law of Motion".
4.2 Newton’s First Law of Motion
An object at rest remains at rest, and an object in motion
remains in motion, unless acted on by a net external force.
In other words, an object maintains its velocity (both speed
and direction) unless acted upon by a nonzero net force.
Having zero velocity, being at rest, is not special, it is just one
possible velocity…a velocity which is no more special than
any other.
4.2 Newton’s First Law of Motion
3) The net force on an object is the vector sum
of all forces acting on that object.
The SI unit of force is the Newton (N).
Individual Forces
4N
10 N
Net Force
6N
Net Force:
Mathematically, the net force is
written as
Fnet or F
where the Greek letter sigma denotes
the vector sum.
1
In the absence of an external force, a moving
object will
c
A
stop immediately.
c
B
slow down and eventually come to a stop.
c
C
go faster and faster.
c
D
move with constant velocity.
Ans: D
2
When the rocket engines on a spacecraft are
suddenly turned off while traveling in empty space,
the starship will
c
A
stop immediately.
c
B
slowly slow down, and then stop.
c
C
go faster and faster.
c
D
move with constant velocity.
Ans: D
3
A rocket moves through empty space in a straight
line with constant speed. It is far from the
gravitational effect of any star or planet. Under
these conditions, the force that must be applied to
the rocket in order to sustain its motion is
c
A
equal to its weight.
c
B
equal to its mass.
c
C
dependent on how fast it is moving.
c
D
zero.
Ans: D
4
You are standing in a moving bus, facing forward,
and you suddenly fall forward. You can infer from
this that the bus‘s
c
A
velocity decreased.
c
B
velocity increased.
c
C
speed remained the same, but it's turning to
the right.
c
D
speed remained the same, but it's turning
to the left.
Ans: A
5
You are standing in a moving bus, facing forward,
and you suddenly fall forward as the bus comes to
an immediate stop. What force caused you to fall
forward?
c
A
gravity
c
B
normal force due to your contact with the floor
of the bus
c
C
force due to friction between you and the
floor of the bus
c
D
There is not a force leading to your fall.
Ans: D
4.2 Newton’s First Law of Motion
4) Inertia is the natural tendency of an
object to remain at rest or in motion at
a constant speed along a straight line
(constant velocity).
Inertia is the resistance of any physical object to any
change in its state of motion, including changes to its
speed and direction.
The mass of an object is a quantitative
measure of inertia.
4.2 Newton’s First Law of Motion
5) All Newton's laws are only valid in
inertial reference frames
An inertial reference frame is one which is
not accelerating or rotating.
It is a space in which every body remains in a state of rest
unless acted on by an external unbalanced force.
Newton’s First Law is also called Law of inertia
6) Relative Motion
• Relative motion – motion depends on your frame
of reference
• Are you moving if you are sitting 100% still in your
chair??
– YES! The earth is moving and you are on the earth,
so you are moving relative to the other planets, the
sun, etc.
– NO! Relative to the floor, you are not moving
– It all depends on your frame of reference
– http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=
140
Check your understanding
http://www.physicsclassroom.com/getattachment/curriculum/ne
wtlaws/newtl2.pdf
http://www.physicsclassroom.com/class/newtlaws/Lesson1/Inertia-and-Mass
4.3 Newton’s Second Law of Motion
4.3 Newton’s Second Law of Motion
When a net external force acts on an object
of mass m,
the acceleration that results is directly
proportional to the net force and has
a magnitude that is inversely proportional to
the mass.
The direction of the acceleration is
the same as the direction of the net force.
F
a
m
F ma
4.3 Newton’s Second Law of Motion
SI Unit for Force
m kg m
kg 2 2
s
s
Fnet ma
4.3 Newton’s Second Law of Motion
4.4 Free body diagram
A free-body-diagram is a diagram that
represents the object and the forces that
act on it.
4.3 Newton’s Second Law of Motion
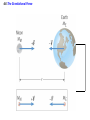
The net force in this case is:
275 N + 395 N – 560 N = +110 N
and is directed along the + x axis of the coordinate system.
4.3 Newton’s Second Law of Motion
If the mass of the car is 1850 kg then, by
Newton’s second law, the acceleration is
F 110 N
a
0.059 m s
m
1850 kg
2
Rules for free body diagram:
1. Identify the object--represent
the object by a box or a circle
2. draw the force arrow from the
object outward in the direction
that the force is acting.
3. label each force arrow
according to its type.
4. Choose coordinate direction.
https://phet.colorado.edu/en/simulation/forces-and-motion-basics
https://phet.colorado.edu/en/simulation/forces-1d
https://phet.colorado.edu/en/simulation/forces-and-motion
6
A 3.5 kg object experiences an acceleration of 0.5
2
m/s . What net force does the object feel?
7
A 12 N net force acts on a 36 kg object? How
much does it accelerate?
8
How much net force is required to accelerate a
0.5 kg toy car, initially at rest to a velocity of 2.4
m/s in 6 s?
9
A net force F accelerates a mass m with an
acceleration a. If the same net force is applied to
mass 2m, then the acceleration will be
c
A
4a
c
B
2a
c
C
a/2
c
D
a/4
10
A constant net force acts on an object. The object
moves with:
c
A
constant acceleration
c
B
constant speed
c
C
constant velocity
c
D
increasing acceleration
11
A net force F acts on a mass m and produces an
acceleration a. What acceleration results if a net
force 2F acts on mass 4m?
c
A
a/2
c
B
8a
c
C
4a
c
D
2a
12
The acceleration of an object is inversely
proportional to:
c
A
the net force acting on it.
c
c
c
B
its position.
C
D
its velocity.
its mass.
Newton’s Second Law of Motion
ΣF
Example: A 5.0 kg object is being acted on by a 20N force to
the right (F1), and a 30N force, also to the right (F2). What is
the net force on the object?
F2
F1
The second force, F2, acts to the right also, with a greater
magnitude of 30N. This is drawn slightly larger than F1.
Newton’s Second Law of Motion
ΣF
Example: A 5.0 kg object is being acted on by a 20N force to
the right (F1), and a 30N force, also to the right (F2). What is
the net force on the object?
To add vectors, move
the second vector so it
starts where the first
one ends.
F1
F2
The sum is a vector which starts where the first vector started,
and ends where the last one ends.
Newton’s Second Law of Motion
ΣF
Example: A 5.0 kg object is being acted on by a 20N force to
the right (F1), and a 30N force, also to the right (F2). What is
the net force on the object?
These free body diagrams are critically important to our
work. Once done, the problem can be translated into an
algebra problem.
ΣF
F1
F2
Newton’s Second Law of Motion
For example: A 5.0 kg object is being acted on by a 20N
force to the right (F1), and a 30N force, also to the right (F2).
What is the net force on the object?
ΣF
F1
F2
First we will define "to the right" as positive.
Then we can interpret our diagram to read:
ΣF = F1 + F2
ΣF
= 20N + 30N
ΣF = 50N to the right
we get the direction from our diagram and from our positive answer,
which we defined as meaning "to the right"
13
Two forces act on an object. One force is 40N to
the west and the other force is 40N to the east.
What is the net force acting on the object?
14
Two forces act on an object. One force is 8.0
N to the north and the other force is 6.0N to the
south. What is the net force acting on the object?
c
A
14 N to the north
c
B
14 N to the south
c
C
2 N to the north
c
D
2 N to the south
Newton’s Second Law of Motion
For example: A 5.0 kg object is being acted on by a 20N
force to the right (F1), and a 30N force, also to the right (F2).
We found the net force on the object to be 50N to the right.
Now let's find its acceleration.
ΣF
F1
F2
ΣF = ma
Answer
a = ΣF
/m
a = 50N / 5.0 kg
2
2
a = 10 m/s to the right s to the right
4.3 Newton’s Second Law of Motion
Force is a vector, so ΣF = ma is true along each coordinate axis.
F1
F3
a = 1 m/s
2
F2
That means we can add up all the forces in the vertical direction
and those will equal "ma" in the vertical direction.
F1
F1 +(-F2) = m*a
F2
F1 - F2 = 0
And then can do the same thing in the horizontal direction.
F3 = m*a
F3
2
a = 1 m/s
2
F3 = (2kg)(1 m/s )
F3 = 2 N
15
A force F1 = 50N acts to the right on a 5.0 kg
object. Another force, F2 = 30N, acts to the left.
Find the acceleration of the object:
16
A force F1 = 350N pushes upward on 20.0 kg
object. Another force, F2 = 450N pulls
downward.
Find the acceleration of the object:
17 An object accelerates downward at a rate of 4.9
2
m/s . If the downward force on the object is 500N
and the upward force is 250N, what is the mass
of the object?
4.5 Newton’s Third Law of Motion
Whenever one body exerts a force on a
second body, the second body exerts an
oppositely directed force of equal magnitude
on the first body.
For every action, there is an equal, opposite reaction. This is
another way to state Newton's 3rd Law.
It is important to remember that the forces (or actions) are
always applied to two different objects.
About action and reaction force:
• All forces come in action-reaction pairs
• Action and reaction forces are equal in
size
• Action and reaction forces are opposite
in direction
• They are same type of force
• They acted on different objects
• will never cancel out each other
Newton’s Third Law of Motion
A key to the correct application of the third law is that the
forces are exerted on different objects.
Make sure you don’t use them as if they were acting on the
same object. Then they would add to zero!
Force on
hands
Force on
floor
4.5 Newton’s Third Law of Motion
Suppose that the magnitude of the force is 36 N. If the mass
of the spacecraft is 11,000 kg and the mass of the astronaut
is 92 kg, what are the accelerations?
4.5 Newton’s Third Law of Motion
F P.
On the astronaut F P.
On the spacecraft
Acceleration of spacecraft:
P
36 N
as
0.0033 m s 2
ms 11,000 kg
Acceleration of astronaut:
P 36 N
2
aA
0.39 m s
mA
92 kg
Newton’s Third Law of Motion
Rocket propulsion can also be explained using Newton’s third law.
Hot gases from combustion spew out of the tail of the rocket at high
speeds. The reaction force is what propels the rocket.
Note that the rocket
does not need
anything to “push”
against.
Newton’s Third Law of Motion
Helpful notation: the first subscript is
the object that the force is being
exerted on; the second is the source.
Subscripts help keep your
ideas and equations clear.
FGP = -FPG
Horizontal force
exerted on the
ground by
person's foot
FGP
Horizontal force
exerted on the
person's foot by
ground
FPG
27
When you sit on a chair, the net external force on
you is
c
A
zero.
c
B
dependant on your weight.
c
C
up.
c
D
down.
28
An object of mass m sits on a flat table. The
Earth pulls on this object with force mg, which
we will call the action force. What is the reaction
force?
c
A
The table pushing up on the object with
force mg
c
B
The object pushing down on the table with
force mg
c
C
The table pushing down on the floor with
force mg
c
D
The object pulling upward on the Earth with
force mg
2
9
A 20-ton truck collides with a 1500-lb car and
causes a lot of damage to the car. Since a lot of
damage is done on the car
c
A
the force on the truck is greater then the force
on the car
c
B
the force on the truck is equal to the force
on the car
c
C
the force on the truck is smaller than the
force on the car
c
D
the truck did not slow down during the collision
30
As you are sitting in a chair, you feel the chair
pushing up on you. The reaction force in this
situation is:
c
A
The chair pushing down on the ground
c
B
Gravity pulling down on you
c
C
You pushing down on the chair
c
D
The ground pushing up on the chair
31
A student is doing push-ups in gym class. A
reaction pair of forces is best described as:
c
A
The student pushes down on the ground The ground pushes up on the student
c
B
Gravity is pulling the student down The ground is pushing the student up
c
C
Gravity is pulling the student down The student's arms push the student up
c
D
The student's hands push down on the ground The students arms push the student up
33
If you blow up a balloon, and then release it, the
balloon will fly away. This is an illustration of:
(Note: there may be more than one answer. Be
prepared to explain WHY!)
c
A
Newton's first law
c
B
Newton's second law
c
C
Newton's third law
c
D
Galileo's law of inertia
4.5 Types of Forces: An Overview
In nature there are two general types of forces,
fundamental and nonfundamental.
Fundamental Forces
1. Gravitational force
2. Strong Nuclear force
3. Electroweak force
4.6 Types of Forces: An Overview
Examples of nonfundamental forces:
Friction force
tension in a rope
normal or support forces
4.6 Gravitational force,
Weight, apparent weight
and Normal Force
1) The Gravitational Force
Newton’s Law of Universal Gravitation
Every particle in the universe exerts an attractive force on every
other particle.
A particle is a piece of matter, small enough in size to be
regarded as a mathematical point.
The force that each exerts on the other is directed along the line
joining the particles.
1) The Gravitational Force
For two particles that have masses m1 and m2 and
are separated by a distance, then there will be
gravitational force acting on each mass by the
other,
4.6 The Gravitational Force
2) Weight – the Force of Gravity
Weight is the force exerted on an object by gravity. Close to
the surface of Earth, where the gravitational acceleration is
nearly constant, weight can be calculated with:
Fg = mg
2
Near the surface of Earth, g is 9.8 m/s downwards.
4.6.2 weight
The weight of an object on or above the earth is the
gravitational force that the earth exerts on the object.
The weight always acts downwards, toward the center
of the earth.
On or above another astronomical body, the weight is the
gravitational force exerted on the object by that body.
SI Unit of Weight: newton (N)
18
Determine the Force of Gravity (weight) of a 6.0 kg
bowling ball.
19
Determine the weight of a small car with a
mass of 900 kg.
20
Using a spring scale, you find that the weight
of a friction block in the lab is around 24 N.
What is the mass of the block, in kilograms?
21
A 120 lb woman has a mass of about 54.5 kg.
What is her weight?
22
What is the weight of a 25 kg object located
near the surface of Earth?
23
Which of the following properties of an object
is likely to change on another planet?
c
A
Mass
c
B
Weight
c
C
Color
c
D
Volume (size and shape)
24
The acceleration due to gravity is lower on the
Moon than on Earth. Which of the following is
true about the mass and weight of an astronaut
on the Moon's surface, compared to Earth?
c
A
Mass is less, weight is same
c
B
Mass is same, weight is less
c
C
Both mass and weight are less
c
D
Both mass and weight are the same
3) Normal Force
An object at rest must have no net force on it. If it is sitting on a
table, the force of gravity is still there; what other force is
there?
FG
Normal Force
An object at rest must have no net force on it. If it is sitting on a
table, the force of gravity is still there; what other force is
there?
The force exerted perpendicular
to a surface is called the normal
force.
It is exactly as large as needed
to balance the force from the
object (if the required force gets
too big, something breaks!)
The words "normal" and
"perpendicular" are synonyms.
FN
FG
25
A 14 N brick is sitting on a table. What is the normal
force supplied by the table?
c
A
14 N upwards
c
B
28 N upwards
c
C
14 N downwards
c
D
28 N downwards
26
What normal force is supplied by a desk to a
2.0 kg box sitting on it?
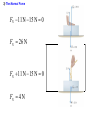
3) The Normal Force
FN 11 N 15 N 0
FN 26 N
FN 11 N 15 N 0
FN 4 N
4) Apparent Weight
The apparent weight of an object is the reading of the scale.
It is equal to the normal force the man exerts on the scale.
The Normal Force
F
y
FN mg ma
FN mg ma
apparent
weight
true
weight
4.7
Friction
Static and Kinetic Frictional Forces
Friction - A Resistive Force
There are many different types of forces that occur in nature,
but perhaps none is more familiar to us than the force of
friction (Ffr).
Friction is a resistive
force that opposes the
motion of an object.
What does sandpaper
have to do with friction?
Friction is resistance to the relative or
tendency of relative motion between the
object and the contact surface.
Friction - A Resistive Force
Friction is the reason objects stop rolling or sliding along a
surface. It is the reason it is difficult to start pushing a heavy
box along the floor.
There are many different
types of friction:
Friction between solid
objects and air is often
called air resistance.
Friction between two
fluids is called viscosity,
and so on.
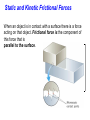
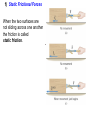
Static and Kinetic Frictional Forces
When an object is in contact with a surface there is a force
acting on that object. Frictional force is the component of
this force that is
parallel to the surface.
1) Static Frictional Forces
When the two surfaces are
not sliding across one another
the friction is called
static friction.
Static Frictional Forces
The magnitude of the static frictional force can have any value
from zero up to a maximum value.
fs f
f
0 s
MAX
s
MAX
s
s FN
is called the coefficient of static friction.
4.9 Static and Kinetic Frictional Forces
Note that the magnitude of the frictional force does
not depend on the contact area of the surfaces.
2) Kinetic Frictional Forces
While Static friction opposes the impending relative motion
between two objects.
Kinetic friction opposes the relative sliding motion motions
that actually does occur.
f k k FN
0 k
is called the coefficient of kinetic friction.
4.7 Static and Kinetic Frictional Forces
4.7 Static and Kinetic Frictional Forces
The sled comes to a halt because the kinetic frictional force
opposes its motion and causes the sled to slow down.
4.7 Static and Kinetic Frictional Forces
Suppose the coefficient of kinetic friction is 0.05 and the total
mass is 40kg. What is the kinetic frictional force?
f k k FN k mg
0.0540kg 9.80 m s 20N
2
Example:
The force of friction between an object and the surface upon which it is sliding is
8 N. The mass of the object is 20kg.
How much is the object’s weight?
How much is the normal force?
What is the coefficient of kinetic friction?
Example:
The minimum horizontal force to move an object on a surface is 400N. The
force of friction between an object and the surface upon which it is sliding is
360N. The mass of the object is 95kg. What is the coefficient of kinetic friction?
What is the coefficient of static friction?.
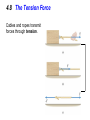
4.8 The Tension Force
Cables and ropes transmit
forces through tension.
4.8 The Tension Force
A massless rope will transmit
tension undiminished from one
end to the other.
If the rope passes around a
massless, frictionless pulley, the
tension will be transmitted to
the other end of the rope
undiminished.
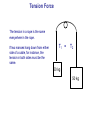
Tension Force
The tension in a rope is the same
everywhere in the rope.
If two masses hang down from either
side of a cable, for instance, the
tension in both sides must be the
same.
T1 =
T2
20 kg
50 kg
4.9 Air resistance force--Fair
• special type of frictional force
• oppose the motion of an object
• It is most noticeable for objects that travel
at high speeds
• Usually is speed related.
4.10 Spring force--Fspring
• force exerted by a compressed or
stretched spring upon any object that is
attached to it
• to its rest or equilibrium position
• Hook’s Law-magnitude of the force is
directly proportional to the amount of
stretch or compression of the spring
Practice of free body diagram
and problem solving
1. Select a “object”("system“) to which you intend
to apply Newton's Second Law.
2. Draw free body diagram, identify all forces
3. Pick a coordinate system. Find out forces
relations and list them out
4. Find what you need to solve and which what
relations needed
5. Write Newton's Second Law, and equations
6. Solve equations
4.11 Equilibrium Application of Newton’s
Laws of Motion
Definition of Equilibrium
An object is in equilibrium when it has zero acceleration.
F F
net
0
4.12 Force at Angles-- When force vector has an
angle to coordinate direction:
Assume that the
chain is exerting
a 60 N force
upon Fido at an
angle of 40
degrees above
the horizontal
http://www.physicsclassroom.com/class/vectors/Lesson-3/Resolution-of-Forces
4.12 Vector nature of force -- When force vector has an angle to coordinate direction:
Consider the tow truck at the
right. If the tensional force in the
cable is 1000 N and if the cable
makes a 60-degree angle with
the horizontal, then what is the
vertical component of force that
lifts the car off the ground?
The vertical component can be found if a triangle is
constructed with the 1000 N diagonal force as the
hypotenuse. The vertical component is the length
of the side opposite the hypotenuse. Thus,
sin (60o) = (Fvert) / (1000 N)
Solving for Fvert will give the answer 866 N.
4.12 Vector nature of force -- When force vector
has an angle to coordinate direction:
Example:
A 10.0 kg box is pulled along a horizontal surface by a rope that
makes a 30.0o angle with the horizontal. The tension in the rope
is 30.0 N. There is 10.0 N of friction acting on the box. Find:
a) the acceleration of the box
b) The normal force of the ground
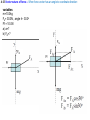
4.12 Vector nature of force -- When force vector has an angle to coordinate direction:
variables:
m=10.0kg
FA= 30.0N, angle θ= 30.0o
Ff = 10.0N
a) a=?
b) FN=?
FN
FN
Ff
Ff
4.12 Vector nature of force -- When force vector has an angle to coordinate direction:
FN
Ff
4.12 connected objects
eg. Two blocks, with masses m1 = 0.4kg and m2 =
0.6kg, are connected by a string and lie on a
frictionless tabletop. A force F = 3.5 N is applied to
block m2.
a. Draw a free-body diagram for each block showing
all applied forces to scale. Next to each diagram
show the direction of the acceleration of that object.
b. Find the acceleration of each object.
c. Find the tension force in the string between two
objects.
m1 = 0.4kg, m2 = 0.6kg, frictionless tabletop.
Fapp = 3.5 N on m2.
Key: both blocks have the same acceleration (motion)
a. free-body diagram for each block.
FN2
FN1
Ften
Fg1
Fapp
Ften
Fg2
b. Find the acceleration of each object.
Two blocks, with masses m1 = 400 g and m2 = 600 g, are
connected by a string and lie on a frictionless tabletop. A
force F = 3.5 N is applied to block m2.
c. Find the tension force in the string between two
objects.
15 kg
12 kg
# 79. A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is suspended
from the other end of the rope. The system is released from rest.
a. Draw a free-body diagram for each object showing all applied
forces in relative scale. Next to each diagram show the
direction of the acceleration of that object.
b. Find the acceleration of each mass.
c. What is the tension force in the rope?
d. What distance does the 12 kg load move in the first 3 s?
e. What is the velocity of 15 kg mass at the end of 5 s?
A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is
suspended from the other end of the rope. The system is
released from rest.
a. Draw a free-body diagram for each object showing all
applied forces in relative scale. Next to each diagram
show the direction of the acceleration of that object.
A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is
suspended from the other end of the rope. The system is
released from rest.
b. Find the acceleration of each mass.
A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is
suspended from the other end of the rope. The system is
released from rest.
c. What is the tension force in the rope?
A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is
suspended from the other end of the rope. The system is
released from rest.
d. What distance does the 12 kg load move in the first 3 s?
A 12 kg load hangs from one end of a rope that passes over
a small frictionless pulley. A 15 kg counterweight is
suspended from the other end of the rope. The system is
released from rest.
e. What is the velocity of 15 kg mass at the end of 5 s?
500 g
300 g
#81. A 500 g block lies on a horizontal tabletop. The coefficient of kinetic
friction between the block and the surface is 0.25. The block is connected
by a massless string to the second block with a mass of 300 g. The string
passes over a light frictionless pulley as shown above. The system is
released from rest.
a. Draw clearly labeled free-body diagrams for each of the 500 g and the
300g masses. Include all forces and draw them to relative scale. Draw
the expected direction of acceleration next to each free-body diagram.
b. Use Newton’s Second Law to write an equation for the 500 g mass.
c. Use Newton’s Second Law to write an equation for the 300 g mass.
d. Find the acceleration of the system by simultaneously solving the
system of two equations.
e. What is the tension force in the string?
500 g
300 g
A 500 g block lies on a horizontal tabletop. The coefficient of
kinetic friction between the block and the surface is 0.25.
The block is connected by a massless string to the second
block with a mass of 300 g. The string passes over a light
frictionless pulley as shown above. The system is released
from rest.
a. Draw clearly labeled free-body diagrams for each of the
500 g and the 300g masses. Include all forces and draw
them to relative scale. Draw the expected direction of
acceleration next to each free-body diagram.
500 g
300 g
A 500 g block lies on a horizontal tabletop. The coefficient of
kinetic friction between the block and the surface is 0.25.
The block is connected by a massless string to the second
block with a mass of 300 g. The string passes over a light
frictionless pulley as shown above. The system is released
from rest.
b. Use Newton’s Second Law to write an equation for the
500 g mass.
500 g
300 g
A 500 g block lies on a horizontal tabletop. The coefficient
of kinetic friction between the block and the surface is 0.25.
The block is connected by a massless string to the second
block with a mass of 300 g. The string passes over a light
frictionless pulley as shown above. The system is released
from rest.
c. Use Newton’s Second Law to write an equation for
the 300 g mass.
500
g
300
g
A 500 g block lies on a horizontal tabletop. The coefficient of
kinetic friction between the block and the surface is 0.25.
The block is connected by a massless string to the second
block with a mass of 300 g. The string passes over a light
frictionless pulley as shown above. The system is released
from rest.
d. Find the acceleration of the system by simultaneously
solving the system of two equations.
500 g
300 g
A 500 g block lies on a horizontal tabletop. The coefficient of
kinetic friction between the block and the surface is 0.25.
The block is connected by a massless string to the second
block with a mass of 300 g. The string passes over a light
frictionless pulley as shown above. The system is released
from rest.
e. What is the tension force in the string?
**
An elevator (mass 4850 kg) is to be designed so that the
maximum acceleration is 0.0680g. What are the
maximum and minimum forces the motor should exert
on the supporting cable?
Two boxes are connected by a cord. A person pulls
horizontally on box A with force F = 40.0 N. The boxes
have masses of 10 kg and 12 kg. Ignore friction
between the boxes and the tabletop.
a) Show the free-body diagram of the box B.
b) Show the free-body diagram of the box A.
c) Find the acceleration of the system.
d) Find the tension in the cord.
mB =
12
kg
mA =
10
kg
FT = 40
N
Two boxes are connected by a cord. A person pulls
horizontally on box A with force F = 40.0 N. The boxes have
masses of 10 kg and 12 kg. Ignore friction between the
boxes and the tabletop.
a) Show the free-body diagram of the box B.
Two boxes are connected by a cord. A person pulls
horizontally on box A with force F = 40.0 N. The boxes have
masses of 10 kg and 12 kg. Ignore friction between the
boxes and the tabletop.
b) Show the free-body diagram of the box A.
Two boxes are connected by a cord. A person pulls
horizontally on box A with force F = 40.0 N. The boxes have
masses of 10 kg and 12 kg. Ignore friction between the
boxes and the tabletop.
c) Find the acceleration of the system.
Given:
mB = 12 kg
mA = 10 kg
Fapp = 40 N 2
g = 9.8 m/s
a=?
Two boxes are connected by a cord. A person pulls
horizontally on box A with force F = 40.0 N. The boxes have
masses of 10 kg and 12 kg. Ignore friction between the
boxes and the tabletop.
d) Find the tension in the cord.
Given:
mB = 12 kg
mA = 10 kg
Fapp = 40 N 2
g = 9.8 m/s 2
a = 1.82 m/s
Two masses are suspended over a pulley by a
cable, as shown on the diagram. Let the mass
of the elevator be 1150 kg and the
counterweight 1000 kg.
a
E
Elevator
car
a) Show the free-body diagram of the elevator
b) Show the free-body diagram of the
counterweight
aC
mE =
1150 kg
c) Calculate the acceleration of the system
Counterweight
mC = 1000 kg
d) Calculate the tension in the cable
Two masses are suspended over a pulley by a cable, as shown
on the diagram. Let the mass of the elevator be 1150 kg and
the counterweight 1000 kg.
a) Show the free-body diagram of the elevator
a
E
Elevator
car
a
mE =
1150 kg
C
Counterweight
mC = 1000 kg
Two masses are suspended over a pulley by a cable, as
shown on the diagram. Let the mass of the elevator be 1150
kg and the counterweight 1000 kg.
b) Show the free-body diagram of the counterweight
aE
Elevator
car
mE =
1150 kg
aC
Counterweight
mC = 1000 kg
Two masses are suspended over a pulley by a cable, as
shown on the diagram. Let the mass of the elevator be 1150
kg and the counterweight 1000 kg.
c) Calculate the acceleration of the system
aE
Elevator
car
mE =
1150 kg
aC
Counterweight
mC = 1000 kg
Two masses are suspended over a pulley by a cable, as
shown on the diagram. Let the mass of the elevator be 1150
kg and the counterweight 1000 kg.
d) Calculate the tension in the cable
aE
Elevator
car
mE =
1150 kg
aC
Counterweight
mC = 1000 kg
Two boxes are connected by a cord
running over a pulley. The
coefficient of kinetic friction
between box A and the table is 0.2
5.0 kg
A
a) Show the free-body diagrams of
box A and box B
B
2.0 kg
b) Find the acceleration of the
system of two boxes
c) Find the tension in the cord
Two boxes are connected by a cord running over a pulley.
The coefficient of kinetic friction between box A and the table
is 0.2
a) Show the free-body diagrams of box A and box
B
5.0 kg
A
B
2.0 kg
Two boxes are connected by a cord running over a pulley.
The coefficient of kinetic friction between box A and the
table is 0.2
b) Find the acceleration of the system of two boxes
Given:
mA = 5 kg
mB = 2 kg 2
g = 9.8 m/s
μ = .2
a=?
5.0 kg
A
B
2.0 kg
Two boxes are connected by a cord running over a pulley.
The coefficient of kinetic friction between box A and the
table is 0.2
c) Find the tension in the cord
Given:
mA = 5 kg
mB = 2 kg
g = 29.8
m/s
μ = .2
a = 1.4
2
m/s
T=?