Download Implementation of Space Vector Modulation Strategies for Voltage

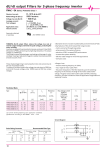
Implementation of Space Vector
Modulation Strategies for Voltage Source
Inverters for Induction Motor Drives
Krisztina Leban1, Cristian Lascu2, Alin Argeseanu3
1
Student at“Politehnica” University of Timisoara, Bd. Vasile Parvan nr.1, Timisoara Romania.
E-mail: [email protected]
Dpt. of Electrical Engineering, “Politehnica” University of Timisoara, Romania
Tel: +40 256 403463, E-mail: [email protected]
2
Dpt. of Electrical Engineering, “Politehnica” University of Timisoara, Romania
Tel: +40 256 403457, E-mail: [email protected]
3
Abstract
This paper reports on a DSP implementation of a space vector pulse-width modulation
technique for three-phased voltage source inverters working with high switching
frequencies in order to generate less harmonic distortion in the output voltages or
current in the motor windings. This strategy provides more efficient use of the DC bus
voltage in comparison with the direct sinusoidal modulation technique. Also a
comprehensive comparison between the implementation of the space vector
modulation and the carrier based PWM generation will be pointed out.
A standard application for this method is the speed control of induction machines. Thus
the induction machine can be smoody started with the help of the ratio
voltage/frequency held constant. The control strategy relies on a simplified machine
model. The values of switching time durations are obtained by real-time calculations
for each period using an optimal algorithm and the proprieties of the sinusoidal wave
forms.
The generated first harmonic output gets ever closer to the sinusoidal wave when the
switching frequency is raised. The maximum value of the transistor’s switching
frequency is determined in deal with the required computing time for each applied
method. The imposed frequency is around 10 kHz.
With the help of the TMS320F2812, a new and complex digital signal processor, the
needed pulse width modulation can be obtained in various ways. This programming
flexibility is achieved with the CODE COMPOSER STUDIO version 3.1 and C++ code
(in witch the software is written). The programme allows offline graphical
representation of the parameters, thus giving a preview of the generated waveforms.
Keywords: Digital Signal Processor(DSP) Implementation, Voltage Source
Inverter(VSI), Space Vector Modulation (SVM), Duty Cycles, Pulse Width Modulation
(PWM), AC Drives
1
1. Voltage Source Inverters (VSI)
The three-phase voltage-fed inverter bridge (Figure 1) has a constant Vdc source
and it is composed of three “legs”: a, b, c, each of them containing two switching power
devices and two return current diodes. The diodes must be able to provide an
alternative path for the inductive current that continues to flow when the power devices
(T1, T2, T3, T4, T5, and T6) are turned off. The upper and lower switches are
controlled complementarily, which means that when the upper one is turned on, the
lower one must be turned off and vice versa. As the power device’s turn-off time is
longer than its turn-on time, some dead time must be inserted between the turn-off of
one transistor of the half-bridge and the turn-on of its complementary device. The
output voltage is mostly created by a Pulse Width Modulation (PWM). In order to
simplify and liberalize the inverter model, the following hypotheses are assumed first
[2]:

The DC link voltage Vdc is considered constant or slowly variable. In general, the
inverter switching frequency is much higher than the frequency of the link voltage
ripples. This assumption is always realistic.

The power switching devices are assumed identical. The reverse recovery current
associated with the diodes turn-off process is neglected.

The switching process is considered ideal, with rise time, fall time and reverse recovery
time incorporated into Ton and Toff times, respectively.

The voltage drop of the power devices is neglected if not otherwise specified.

The device’s dead times are neglected if not otherwise specified.
Figure 1 Voltage Source Inverter
The output 3-phase voltage waves are shifted 120o to each other and thus a 3-phase
motor can be supplied. Let’s define the switching signals Sa , Sb , Sc as binary numbers
that describe the state of each transistor:
Sx  1
Sx  0
if the upper transistor of the leg x is on
if the lower transistor of the leg x is on
2

1, if T2 k 1 is on

Sx  
0, if T is on

2k
(1)
where k  1, 2,3 x  a, b, c
With these signals, the instantaneous line to line voltages are[2]:
uab  Vdc ( Sa  Sb )
ubc  Vdc (Sb  Sc )
uca  Vdc (Sc  Sa )
(2)
Instantaneous phase voltages are:
1
ua  Vdc ( S a  ( S a  Sb  Sc )) ,
3
1
1
ub  Vdc ( Sb  ( S a  Sb  Sc )) , uc  Vdc ( Sc  ( S a  Sb  Sc ))
3
3
u0  ua  ub  uc  0
if the zero sequence voltage is
(3)
The voltage space vector will be:
V  V  jV
,
1
V  Vdc ( S a  ( S a  Sb  Sc ))
3
,
V  Vdc
1
( Sb  Sc )
3
(4)
2. Space Vector Modulation
Space Vector PWM refers to a special switching sequence of the three phased
inverter’s power transistors. (Figure 1). This method has been known to generate less
harmonic distortion in the output voltages and provides more efficient use of the supply
voltage in comparison with direct sinusoidal modulation technique[12]. Eight switching
vectors are obtained with the help of each leg’s switching states –Vx(Sa, Sb, Sc).
Vectors V1 to V6 are called active vectors active vectors because they produce voltages
at the VSI’s output. V0 and V7 are inactive vectors or zero vectors; they do not produce
output voltages but hey are used in the modulation method( Figure 6). Due to these 8
vectors displaced at 60 as shown in Figure 2, 6 sectors are formed.
Figure 2. Space Vector Modulation
Figure 3. Normalized Reference Voltage
The V* (called the reference vector) vector rotates counter clockwise with the angle
α varying between 0 and 360 degrees. At each moment
V  Va  Vb
*
(5)
When the motor is started the magnitude of V* is Vstart .As the supply voltage is
raised, the magnitude of the vector will grow thus describing an spiral. [5] , [3]
3
Figure 4 The Space Vector Modulation principle. .
Employing a linear coordinate transformation, a normalized reference voltage vector is
2
obtained. The normalized vector’s magnitude is Vdc . (Figure 3)
3
 
 
u *  Re u *  j Im u *
(6)
*
3 V*
3 V
u  u  u2  u  ju 
 j
2 Vdc
2 Vdc
*
*
1
*
*
*
(7)
The duty cycles for each phase are determines:
Ts
Dx 
1
S x dt ,
Ts 0
x = a, b, c
Ts = the period
(8)
Sx = switch state of leg x
Duty cycles for each sectors are the following:
Sector S1
D1  u*  u*
D2  2u*
D0  D7  1  D1  D2
Sector S2
D2  u*  u*
D3  u*  u*
D0  D7  1  D3  D2
Sector S3
D3  2u*
D4  u*  u*
D0  D7  1  D3  D4
Sector S4
D4  u*  u*
D5  2u*
D0  D7  1  D4  D5
Sector S5
D5  u*  u*
D0  D7  1  D5  D6
Sector S6
D6  2u
D6  u*  u*
D1  u*  u*
D0  D7  1  D1  D6
*

Figure 7 Duty Cycles
At even sectors the order of the two non-zero vectors should be changed to avoid
supplementary switching.
4
Figure 7 Application Sequence of Basic Vector
Zero vectors are used to complete the period after the active vectors war applied.
5
The standard programme should contain the following steps:
1.System registers must be set. It is recommended that C++ procedures are defined in
order to write the registers. Please note that some system registers are protected. You
can write C++ enable/disable code using the dedicated assembly procedures listed in
the board’s documentation. An example for this sort of protection is the Watchdog
Counter Register. If you chose to disable it, you should provide other means of
monitoring the continuance of the program flow.
2.Timers. Select a clock (high speed or low speed) and divide it so that the resulted
frequency is the desired one. The period, underflow, overflow and compare will each
trigger interrupts if enabled.
3.Interrupt code. In order for an interrupt routine to be successfully executed you must
have the following in mind:

Define the interrupt vector table in a name.asm file;

Put the interrupt routine ‘s name in earlier defined vector table ;

Enable (globally, locally), unmask and acknowledge the desired interrupts in the
name.c file.

Clear the interrupt flags so that upcoming interrupts will be acknowledged.
The space vector strategy is implemented as an interrupt routine. The algorithm is that
in the Figure 8
Determine the current
sector by the value of the
alpha angle
Calculate Vα and Vβ
Calculate duty cycles
Determine time of
application for the two
adjacent vectors for the
given sector
Set the vector sequence
according to the sector
(Odd or even)
Figure 8 Basic Algorithm Steps for SV PWM
Dead band generation. In order to safely switch the power transistors a dead
time(in witch both power devices of one leg are in an off state) is needed. The
TMS320F2812 DSP has dedicated registers that can be used for this purpose.
6
3. Results
The figures below are obtained for an input DC voltage of 560V and a switching
frequency of 10kHz ; the output frequency is 50Hz/25Hz.
Ualfa*
Ubeta*
Da
Db
Dc
Figure 7 Basic Algorithm Steps for SV PWM, f=50Hz
Ualfa*
Da
Ubeta*
Db
Dc
Figure 8 Basic Algorithm Steps for SV PWM, f=25Hz
7
References
[1] Brian Kernigham, Dennis Ritchie “The C Programming Language. Second edition”
Prentice Hall international, Englewood Cliffs, New Jersey, 1988;
[2]Lascu Cristian “Direct Torque Control Of Sensorless Induction Machine Drives” Ph. D.
Thesis, Timisoara 2002
[3] Krisztina Leban ‘Diploma Project 2007’ Politehnica University of Timisoara, Romania
[4] Joachim Holtz “Pulse width Modulation for Electronic Power Conversion ” Proceedings of
IEEE vol.82, no. 8, August 1994;
[5] Sorin Musuroi, Dorin Popovici “Electric Drives and Servomotors”, Editura Politehnica
2006;
[6] Texas Instruments
Guide,SPRU430
TMS320C28x
DSP
CPU
and
Instruction
Set
Reference
[7] TMS320x281x Analog-to-Digital Converter (ADC) Reference Guide ( SPRU060)
[8] TMS320x280x System Control and Interrupts Reference Guide (SPRU712)
[9] TMS320x281x, 280x Peripheral Reference Guide (SPRU566)
[10] TMS320x281x Event Manager (EV) Reference Guide (SPRU065)
[11] TMS320x281x External Interface (XINTF) Reference Guide (literature Number
SPRU067)
[12] Keliang Zhou and Danwei Wang, Member, IEEE-“Relationship between Space-vector
Modulations and Three-Phase Carrier-Based PWM: A Comprehensive Analysis”
[13] Joachim Holtz, Senior Member, IEEE “Pulse width Modulation-A Survey”
8