Download Red Pasiva de Control de Tono James

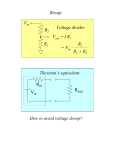
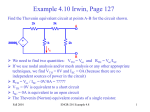
The James-Baxandall Passive Tone-Control Network
Independent adjustment of bass and treble frequencies in high fidelity audio amplifiers
is usually accomplished utilizing specially designed tone-control networks. There are
versions for these tone controls based only on passive components, such as the groundreferenced James network shown in fig. 1. Among those versions using active devices
we must make mention of P.J. Baxandall´s proposal, in which the tone control was
devised as a feedback amplifier (refs. 1 and 2).
In this article we shall analyze the James network (also known as the passive Baxandall
tone control), obtaining its design equations.
Let´s begin studying the bass control section (fig.2), which has influence over the
frequencies below the designed center frequency of the overall James network.
Here, R4 offers some isolation between this stage and the treble control section
(frequencies above the center frequency are affected by this control). R5 represents the
input resistance of the amplifier connected to the output of the James network and
should be selected such that it imposes no appreciable load on the network. Here we
assume that C3 and C4 are open circuits at the bass frequencies.
With full bass boost (R2´s slider at the upper end), the equivalent circuit for the tone
control is as depicted by fig.3.
From this figure and knowing that “s” is Laplace´s variable, we obtain:
V0  Vg
R3  R2 // X C 2
R1  R3  R2 // X C 2
where:
1
sC 2

1
R2 
sC 2
R2 
R2 // X C 2

R2
sR2 C2  1
Then:
R2
sR 2 C 2  1
V0  V g
R2
R1  R3 
sR 2 C 2  1
R3 
After some algebraic work we arrive to:
R2
V0
R3
R3


R2
V g R1  R3
sR 2 C 2  1 
R1  R3
sR 2 C 2  1 
...(1)
The gain for high bass frequencies is:
A1 
R3
R1  R3
The gain at low frequencies is:
A2 
R2  R3
R1  R2  R3
Expression (1) has a zero given by:
R2
R3
s 01  
R2 C 2
1
and a pole:
1
s p2  
R2
R1  R3
R2 C 2
With the tone control adjusted for maximum bass cut (R2´s slider at the lower end), the
equivalent circuit changes to that of fig.4. Again, we neglect the loading effect of R4 and
R5 .
Now the following holds:
V0  Vg
 Vg
R3
R1  R3  R2 // X C1
R3
R1  R3 
R2
sR2 C1  1
A simple algebraic manipulation takes us to:
V0
R3


V g R1  R3
sR2 C1  1
R2
sR2 C1  1 
R1  R3
The gain at high bass frequencies is now given by:
A3 
R3
R1  R3
For low frequencies the gain is:
A4 
R3
R1  R2  R3
Expression (2) has a zero given by:
s 03  
1
R2 C1
...(2)
and a pole:
1
s p4  
R2
R1  R3
R2 C1
The gain ratio at low frequencies is:
A2
R
 1 2
A4
R3
For a 40dB control range the following relationship must be satisfied:
1
R2
 100
R3
...(3)
Then:
R2  99 R3  100 R3
On the other hand, at maximum bass boost, the ratio of the gains for low and high bass
frequencies is:
R 2  R3
R  R 2  R3
A2
 1
R3
A1
R1  R3

R1  R3
R2  R3

R3
R1  R2  R3
According to expression (3):
R2  R3  100R3
Then:
100 R3
A2 R1  R3


A1
R3
R1  100 R3

100R1  R3 
R1  100 R3
For a 20dB bass boost:
100R1  R3 
 10
R1  100 R3
Solving for R1 we arrive to the following relationship:
R1  10R3
We may check that:
A3
R3
R  R2  R3

 1
A4 R1  R3
R3
 10
this is, the ratio of the high-frequency and low-frequency bass gains is also 20dB at
maximum bass cut.
For best symmetry in the response curves we must choose s01 = sp4. Therefore:
1
R2
R3
C2
1

R2
R1  R3
C1
Substituting the already obtained relationships between the resistances yields:
100

C2


Then, C2 = 10C1.
1
R2
11R3
C1
99
11
C1
1
10
C1
The corresponding Bode plot of the bass response at full boost and full cut is shown
below.
Next, we will analyze the treble control. We have already stated that the treble
frequencies are those above the center frequency for which the James network is
designed. We may consider C1 and C2 as short circuits at these frequencies. Therefore,
R1 and R3 along with R4 are part of the treble network (fig.6).
In order to facilitate calculations, we shall first find the Thevenin equivalent for Vg, R1
and R3. In fig.7, the equivalent Thevenin voltage source, V1, is given by:
V1  Vg

R3
R1  R3
Vg
11
...(4)
The equivalent Thevenin resistance, RTH, is:
RTH  R1 // R3
With the treble control adjusted for maximum boost (R6´s slider at the upper end), and
assuming the current through resistor R6 is much smaller than that flowing through R4,
we may state the following:
V1  V0
 V0  Vg sC3
RTH  R4
if R5>>R4.
Substituting the value given by expression (4) for V1:
Vg
 V0
11
 V0  Vg sC 3
RTH  R4
Rearranging this equation we get:
1

V g   sC 3 RTH  R4   V0 1  sC 3 RTH  R4 
11

Then:
1
 sC 3 RTH  R4 
V0 11

Vg
1  sC 3 RTH  R4 
...(5)
At sufficiently low treble-frequencies:
V0
1

Vg 11
the same as -20.83dB.
At sufficiently high treble-frequencies:
V0
1
Vg
or 0dB.
Expression (5) has a zero given by:
s 05  
1
11  RTH  R4 C3
and a pole:
s p6  
RTH
1
 R4 C3
With the treble control adjusted for maximum cut (R6´s slider at the lower end) we may
write:
V1  V0
 sC 4V0
RTH  R4
Then:
V0
1

V1 1  sRTH  R4 C 4
From the above equation and bearing in mind (4):
V0
1

V g 11  1  sRTH  R4 C 4 
...(6)
At sufficiently low treble-frequencies:
V0
1

Vg 11
or -20.83dB.
At sufficiently high treble-frequencies:
V0
0
Vg
Expression (6) has a pole given by:
s p7  
RTH
1
 R4 C 4
For best symmetry in the response curves we must choose sp7 = s05. Therefore:
RTH
1
1

 R4 C 4 11  RTH  R4 C3
yielding C4 = 11C3.
Fig.8 shows the corresponding Bode plot of the treble response at full boost and full cut.
A convenient value for R6 must now be computed. We need some knowledge on the
constraints the network imposes before we may neglect the current through R 6, as
compared to that circulating through R4 (IR6<<IR4). IR4 is given by the following
expression when the treble control is adjusted for full cut:
Vg
I R4
 V0
11

RTH  R4
and IR6 by:
I R6 
V g  V0
1
R6 
sC 3
Therefore, the requirement that must be satisfied is:
Vg
 V0
 11
RTH  R4
1
R6 
sC 3
V g  V0
The worst case for the above inequality occurs when s approaches infinity. Translated to
our analysis, at sufficiently high treble-frequencies. Then, it is required that:
Vg
 V0
R  R4
11
 TH
V g  V0
R6
or equivalently:
1 V0

11 V g RTH  R4

V0
R6
1
Vg
At sufficiently high frequencies:
V0
0
Vg
It is clear then that the following must be satisfied:
1 RTH  R4

11
R6
Then:
R6 11RTH  R4 
...(7)
If we conduct a similar analysis when the treble control is at full boost, we would find
that the condition to be met is R6>>1.1R4. Hence, expression (7) prevails.
We would like to arrive at easy-to-use design formulae, so, before presenting a design
example for the James network we shall try to simplify the expressions for f 01, fp2, f03,
fp4, f05, fp6 and fp7. First, for convenience, the relationships between the components’
values will be repeated. These are:
R1 = 10R3
R2 = 99R3
C2 = 10C1
C4 = 11C3
f01 is given by:
R2
R3
1


2 R2 C 2
1
f 01

1 100

2 R2 C 2

1
100

2 99 R3 C 2

1
1

2 R3 C 2
...(8)
fp2 is given by:
f p2 
1

2
1
R2
R1  R3
R2 C 2

1
10

2 R2 C 2

1
10

2 99 R3 C 2

1
1

2 10 R3 C 2
...(9)
f03 is given by:
f 03 
1
1

2 R2 C1

1
10

2 R2 C 2
 f p2
fp4 = f01, required for the desired symmetry on the response curves.
f05 is given by:
f 05 
1
1

2 11RTH  R4 C3

1
1

2 11R1 // R3  R4 C 3

1

2

1
1

2 10 R3  11R4 C 3
1
 10

11 R3  R4 C3
 11

...(10)
fp6 is given by:
f p6 
1
1

2 RTH  R4 C 3
 11 f 05
fp7 = f05, required for the desired symmetry on the response curves.
The center frequency of the James network is taken as the geometric mean of f01 and
f05, this is:
fc 
f 01  f 05
...(11)
which coincides with the frequency of the minimum of the amplitude response curve
when the bass and treble controls are at full boost. Agrees also with the frequency of the
maximum of the amplitude response curve when both controls are at full cut. Usually,
1kHz is adopted as the center frequency.
A Design Example
Let us suppose we wish to design a tone control for a transistorized piece of equipment.
An adequate value for R1 is 10k ohms. R3 will then be a 1k ohm-resistor and R2 a 100k
ohm-potentiometer (standard value).
It is convenient that f01 and f05 be separated one decade in frequency. Then, from
expression (11) we may obtain that:
f c  10 f 01
Being fc = 1kHz, we find that f01 must be 316Hz. The value for f05 will then be
3.16kHz.
From expression (8) we obtain for C2 a value of 503.65nF. Then, C1 should have a
capacitance of 50.36nF. According to (9), fp2 = 31.6Hz.
R5 is taken equal to 5 times R2 in order to avoid loading effects on the bass network.
Therefore, R5 = 500k ohms. R4 must be chosen such that an affordable value for R6 is
obtained when using inequality (7). If we make R4 = 5k ohms, then R6 must satisfy the
condition R6>>65k ohms. We may adopt a value of 500k ohms for R6.
From expression (10), with the value chosen for R4 we obtain C3 = 774.85pF and C4 =
8.52nF.
Finally, in order to avoid additional attenuation in the circuit, the output resistance of
generator Vg (source resistance) must be made some 20 times smaller than R1.
Simulation of the frequency response of the James network
Tone Stack Calculator 1.3 is an excellent software program that can be used for
simulation of tone-control networks. It may be downloaded from:
http://www.duncanamps.com/tsc/
Two simulations have been made using this program. The first simulation uses the
above calculated component values and the second one, standard capacitor values for
the circuit. No major variation on frequency response has been observed between them.
Simulation results are shown below.
Fig.9 Frequency response of the James network with the bass and treble controls at full
boost (upper) and full cut (lower).
Fig.10 Frequency response of the James network when standard capacitance values for
C1, C2, C3 and C4 are used.
References
1. Baxandall, P.J. “Negative feedback tone control – independent variation of bass and
treble without switches” W.W. 58.10 (Oct. 1952) 402. Correction 58.11 (Nov. 1952)
444.
2. Vargas Patrón, Ramón “Red activa de control de tono”
http://www.inictel.gob.pe/publicaciones/rvargas/red-activa.htm
Ramon Vargas Patron
[email protected]
Lima-Peru, South America
July 23rd 2004