* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download R 2
Survey
Document related concepts
Transcript
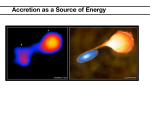
INAF, Osservatorio Astronomico di Roma XI Advanced School of Astrophysics, Brazil, 1-6 September 2002 Summary * Fundamentals of binary evolution: Roche lobe and mass transfer; Timescales of mass transfer; Role of angular momentum losses; Onset of mass transfer in the case of iradiation and its influence on low mass Xray binary secular evolution; Pulsars and the spin-up phase; Modalities of mass transfer towards neutron stars Timescales relevant to evolution • Nuclear tn • Thermal tKH ~GM2/RL • Dynamical td ~(2R3/GM)1/2 For stars it is generally t d << t KH << t n Binary evolution depends on the relation of these quantities with the mass loss timescale t mdot ~M/Mdot The Eddington limit to mass accretion The limiting luminosity which can be produced by accretion is selflimited by a feedback mechanism: namly by the pressure exerted from the radiation produced by accretion against the gravity of the falling matter Roche lobe geometry CM [-GM1/(r1+RL1)2 ] +[GM2/(r2-RL1) 2]+W R =0 2 L1 (reference frame with origin in the mass center, corotating with the system at velocity W=2 p /Porb). RL1 is the distance of L1 from the CM Roche lobe: The smallest closed equipotential surface containing both objects Approximate expressions Definition of Roche lobe radius: It is the radius of the sphere which has the same volume as the Roche lobe of the star. For the “secondary” component in a binary in which q=M2/M1<0.8 (from Paczynski 1971) In binary computations, we use spherical stars, so the evolution is followed by requiring a comparison between stellar radius and Roche lobe radius Total mass and angular momentum evolution If M2/M1<1, the orbital separation a increases with mass transfer. In cases of unevolved mass losing components (e.g. CVs) this implies that the orbital angular momentum can not be constant Gravitational radiation (Landau & Lifshitz 58 Magnetic braking (Verbunt & Zwaan 81) Standard evolution driven by AML: cataclysmic binaries the secondary quasi-MS star evolves first down along the MS, then its radius becomes larger than the MS radius, when tKH~tmdot . Finally the degenerate sequence is reached and the period increases again. Pmin~80m if GR operates Porb- Mdot evolution in CVs Secular evolution: from long to short periods M1=1.4Mo M2=0.8Mo f_VZ=0.7 JMB=0 when M2 becomes fully convective: M2 recovers thermal equilibrium and a Period Gap is established Low mass X ray binaries secular evolution WARNING The orbital periods and type of secondary components are similar to those of CVs, so the first idea is that they evolve similarly, through loss or orbital angular momentum, from long to short periods. Actually this is probably not true! Evolution with mass transfer If R2<R 2,R, no mass transfer. Simplest prescription: R2,=R2,R, enforced in the structure computations. This allows to follow stationary mass transfer phases. Second approximation: Lubow and Shu 1975: subsonical and isothermal mass flow in optically thin layers, reaching sound velocity at L1, or adiabatic in optically thick layers Non stationary mass transfer formulation depends on the donor star parameters, mass, radius Teff, photospheric density Hp ~ 10 –4 R2 for low mass stars: thus the Mdot is a sensitive function of R2R- R2 : R2 must be computed with care Stability of mass transfer . For a general discussion on M see Ritter 1995, in Evolutionary Processes in Binary Stars (CUP) Stationary mass transfer if: z ad zR 2 dln J/ dt Tells which are the system angular momentum primary losses The denominator terms can enhance Mdot by destabilizing it Includes all the terms: nuclear expansion, thermal relaxation, illumination The mass transfer with irradiation In some important cases, the secondary star is immerged in the radiation field of the primary and this produces an effect on its radius derivative R2 is < RRL Lirr=Lx in Xray binaries Lirr=L(pulsar) in MSPs “heating” luminosity: Fraction of Lirr impinging The secondary star f = possible screening factor The reaction of convective stars to mass loss If Lh>Lnuc the radiation field shields the star and does not allow to the nuclearly energy generated luminosity to freely escape from the surface. If the star has a convective envelope, it expands on the thermal timescale at its bottom Although the long term effect of illumination is not easy to be understood, the short term effect on the onset of mass transfer is clear: mass transfer is enhanced The onset of mass transfer in Xray binaries Mass transfer due to AML begins, with a given Mdot Mdot increases . Lx= GMM/RNS Lh~0.03Lx shields the secondary star, causing a radius increase Runaway? Limitation in Mdot comes from the thermal relaxation of the star Effect of irradiation on the onset of mass transfer M2=0.8Mo in main sequence Full line: with irradiation Dotted: standard evolution Acceleration of mass transfer when illumination is present Onset of mass transfer with irradiation Stationary phase due to balance between thermal relaxation and expansion due to irradiation Mass transfer with irradiation will be subject to instability If, for any reason, there is a shielding of Lx, so that Lh decreases, the radius of the secondary will tend to decrease, Mdot will decrease and, this time, this is a runaway situation and the system detaches The system comes back again to a semidetached stage, but this will occur on the timescale of the systemic AM losses: detached phases may be much longer than mass transfer phases Standard Evolution compared to irradiation Green: CV type evolution Yellow: irradiated evolution Porb increases; Mdot is 10100 times larger How irradiation helps in X-ray binaries •The orbital period increases as observed • The mass loss rate is larger • The number ratio LMXB/MSPs is more reasonable • The system evolves through alternated high Mdot phases and detached phases which may help in explaining why radio MSPs do not accrete too much mass (see later) Disc – Magnetic Field Interaction Disc Pressure . proportional to M Magnetic Pressure Proportional to B2 Pulsars spin up The accreting matter transfers its specific angular momentum (the Keplerian AM at the magnetospheric radius) to the neutron star: L=(GmRm)1/2 The process goes on until the pulsar reaches the keplerian velocity at Rm (equilibrium period) The conservation of AM tells us how much mass is necesssary to reach Peq starting from a non-rotating NS. A trivial approximation gives ~0.9Msun The energy lost in electromagnetic radiation and in the relastivistic particle beam comes from the rotational energy of the pulsar, which slows down Pulsar power . Measuring P and P allows to derive m B~108Gauss for MSPs . M Accretion conditions: 1 (Illarionov & Sunyaev 1975) Accretion regime R(m) < R(cor) • accretion onto NS surface (magnetic poles) • energy release L=GMM(dot)/R* R(m) ~ f RA, f ~1 Accretion conditions: 2 Propeller regime R(cor) < R(m) < R(lc) . M • centrifugal barrier closes (B-field drag stronger than gravity) • matter accumulates or is ejected from R(m) • accretion onto R(m): lower gravitational energy released Accretion conditions: 3 Radio Pulsar regime R(m) > R(lc) . M • no accretion • disk matter swept away by pulsar wind and pressure We have set the stage! In the following, we can talk about the MSP population of globular clusters. Then we go back to our favourite globular cluster and show that it harbors the most incredible pulsar, an MSP in an interacting binary