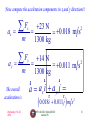* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Wednesday, February 25 , 2009
Equations of motion wikipedia , lookup
Coriolis force wikipedia , lookup
Hooke's law wikipedia , lookup
Classical mechanics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Electromagnetism wikipedia , lookup
Fundamental interaction wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Mass versus weight wikipedia , lookup
Fictitious force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Centrifugal force wikipedia , lookup
Classical central-force problem wikipedia , lookup
PHYS 1441 – Section 002 Lecture #8 Wednesday, Feb. 25, 2009 Dr. Jaehoon Yu • • • • Newton’s Second Law and Third Law Free Body Diagram Categories of forces Application of Newton’s Laws – • Forces of Friction – Wednesday, Feb. 25, 2009 Motion without friction Motion with friction PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 1 Announcements • Quiz Monday, Mar.2 – Beginning of the class – Covers Ch4. or what we finish this Wednesday • Change of Exam Dates – Mid-term exam scheduled on Mar. 11 now moved to Wed. Mar. 27 – Second non-comprehensive exam scheduled on Apr. 13 now moved to Wed. Apr. 22 – Final comprehensive exam stays on the same date, May 11 • Colloquium today Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 2 Special Project for Extra Credit A large man and a small boy stand facing each other on frictionless ice. They put their hands together and push against each other so that they move apart. a) Who moves away with the higher speed and by how much? b) Who moves farther in the same elapsed time? • Derive fomulae for the two problems above in much more detail than what is shown in this lecture note. • Each problem is 10 points each. • Due is Wednesday, Mar. 4. • Please be sure to clearly define each variables used in your derivation. Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 3 Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 4 Vector Nature of the Force The direction of force and acceleration vectors can be taken into account by using x and y components. r r F ma is equivalent to F y Wednesday, Feb. 25, 2009 may F PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu x max 5 Ex. Stranded man on a raft A man is stranded on a raft (mass of man and raft = 1300kg)m as shown in the figure. By paddling, he causes an average force P of 17N to be applied to the raft in a direction due east (the +x direction). The wind also exerts a force A on the raft. This force has a magnitude of 15N and points 67o north of east. Ignoring any resistance from the water, find the x and y components of the rafts acceleration. Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 6 First, let’s compute the net force on the raft as follows: Force r P r A r r r F P A Wednesday, Feb. 25, 2009 x component +17 N y component 0N +(15N)cos67o +(15N)sin67o +17+15cos67o= +23(N) +17+15sin67o= +14(N) PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 7 Now compute the acceleration components in x and y directions!! ax ay F x m F The overall acceleration is Wednesday, Feb. 25, 2009 y m 23 N 2 0.018 m s 1300 kg 14 N 0.011 m s 2 1300 kg r r r a ax i a y j r r 0.018i 0.011 j m s 2 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 8 Example for Newton’s 2nd Law of Motion Determine the magnitude and direction of the acceleration of the puck whose mass is 0.30kg and is being pulled by two forces, F1 and F2, as shown in the picture, whose magnitudes of the forces are 8.0 N and 5.0 N, respectively. ur F1x F 1 cos q1 8.0 cos 60 4.0N Components ur of F1 F1 y F 1 sin q1 8.0 sin 60 6.9N F1 q160o q2-20o F2 ur Components F2 x F 2 cos q2 5.0 cos -20 4.7N ur of F2 F2 y F 2 sin q 2 5.0 sin -20 -1.7N Components of total force F Fx F1x F2 x 4.0 4.7 8.7N max Fy F1 y F2 y 6.9 -1.7 5.2N ma y F 8.7 ax x 29m / s 2 m 0.3 Fy Magnitude and direction of a -1 17 o -1 y tan tan q acceleration a 30 29 a Wednesday, Feb. 25, 2009 x 5.2 ay 17 m / s 2 m 0.3 Acceleration Vector a PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu r 2 2 2 a ax 2 a y 29 17 34m / s 2 r a ax i ay j 29 i 17 j m / s 2 9 Newton’s Third Law (Law of Action and Reaction) If two objects interact, the force F21 exerted on object 1 by object 2 is equal in magnitude and opposite in direction to the force F12 exerted on object 2 by object 1. F12 ur 2 ur F21 F 12 - F 21 1 The action force is equal in magnitude to the reaction force but in opposite direction. These two forces always act on different objects. What is the reaction force to the force of a free falling object? The gravitational force exerted by the object to the Earth! Stationary objects on top of a table has a reaction force (called the normal force) from table to balance the action force, the gravitational force. Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 10 Ex. The Accelerations Produced by Action and Reaction Forces Which one do you think will get larger acceleration? Suppose that the magnitude of the force is 36 N. If the mass of the spacecraft is 11,000 kg and the mass of the astronaut is 92 kg, what are the accelerations? Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 11 Ex. continued r r Force exerted on the space craft by the astronaut F P. r r Force exerted on the astronaut by the space craft F -P. r r P 36 i N space craft’s r 2 a 0.0033m s s acceleration ms 11,000 kg r r - P -36 i N 2 astronaut’s r a 0.39 m s A acceleration m A 92 kg Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 12 Example of Newton’s 3rd Law A large man and a small boy stand facing each other on frictionless ice. They put their hands together and push against each other so that they move apart. a) Who moves away with the higher speed and by how much? F12 F21= - F12 M Since m ur ur F 12 - F 21 Establish the equation Wednesday, Feb. 25, 2009 ur ur F 12 - F 21 ur ur F 12 F 21 F r ur F 12 ma b ur r F 21 M a M F 12 x mabx F 12 y maby 0 F 21x MaMx F Ma 0 21 y and My ur ur F 12 - F 21 F mabx F MaMx Divide by m PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu F M aMx abx m m 13 Example of Newton’s 3rd Law, cnt’d Man’s velocity vMxf vMxi aMxt aMx t Boy’s velocity vbxf vbxi abxt abxt M M aMxt vMxf m m So boy’s velocity is higher than man’s, if M>m, by the ratio of the masses. b) Who moves farther while their hands are in contact? Boy’s displacement 1 M xb vbxi t abx t 2 aMx t 2 2 2m M 1 M 2 xb a t xM Mx m 2 m Man’s displacement Given in the same time interval, since the boy has higher acceleration and thereby higher speed, he moves farther than the man. Wednesday, Feb. 25, 2009 PHYS 1441-002, Spring 2009 Dr. Jaehoon Yu 14 Some Basic Information When Newton’s laws are applied, external forces are only of interest!! Why? Because, as described in Newton’s first law, an object will keep its current motion unless non-zero net external force is applied. Normal Force, n: Reaction force that reacts to action forces due to the surface structure of an object. Its direction is perpendicular to the surface. Tension, T: The reactionary force by a stringy object against an external force exerted on it. Free-body diagram Wednesday, Oct. 1, 2008 A graphical tool which is a diagram of external forces on an object and is extremely useful analyzing forces and motion!! Drawn only on an object. 15 Free Body Diagrams and Solving Problems • 1. 2. 3. 4. 5. 6. Free-body diagram: A diagram of vector forces acting on an object A great tool to solve a problem using forces or using dynamics Select a point on an object in the problem Identify all the forces acting only on the selected object Define a reference frame with positive and negative axes specified Draw arrows to represent the force vectors on the selected point Write down net force vector equation Write down the forces in components to solve the problems No matter which one we choose to draw the diagram on, the results should be the same, as long as they are from the same motion FN M FN Which one would you like to select to draw FBD? What do you think are the forces acting on this object? Gravitational force FG M g Gravitational force Me m The force pulling the elevator (Tension) What about the box in the elevator? Wednesday, Oct. 1, 2008 FG M g the force supporting the object exerted by the floor Which one would you like to select to draw FBD? What do you think are the forces acting on this elevator? FT FN F GB mg FG M g Gravitational force Normal force FT FG M g FN 16 F BG m g Categories of Forces • Fundamental Forces: Truly unique forces that cannot be derived from any other forces – Total of three fundamental forces • Gravitational Force • Electro-Weak Force • Strong Nuclear Force • Non-fundamental forces: Forces that can be derived from fundamental forces – Friction – Tension in a rope – Normal or support forces Wednesday, Oct. 1, 2008 17 The Normal Force The normal force is one component of the force that a surface exerts on an object with which it is in contact – namely, the component that is perpendicular to the surface. Monday, Mar. 3, 2008 PHYS 1441-002, Spring 2008 Dr. Jaehoon Yu 18 Some normal force exercises Case 1: Hand pushing down on the book FN - 11 N - 15 N= 0 FN 26 N Case 2: Hand pulling up the book FN 11 N - 15 N 0 FN 4 N Monday, Mar. 3, 2008 PHYS 1441-002, Spring 2008 Dr. Jaehoon Yu 19 Applications of Newton’s Laws Suppose you are pulling a box on frictionless ice, using a rope. M What are the forces being exerted on the box? T Gravitational force: Fg n= -Fg Free-body diagram n= -Fg T Fg=Mg Normal force: n T Fg=Mg Tension force: T Total force: F=Fg+n+T=T If T is a constant force, ax, is constant Wednesday, Oct. 1, 2008 Fx T Ma x F y ax - Fg n Ma y 0 T M ay 0 v xf vxi a xt v xi T t M 1 T 2 x x v t t x f i xi 2M What happened to the motion in y-direction? 20