* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Simple Harmonic Moti.. - hrsbstaff.ednet.ns.ca
Survey
Document related concepts
Transcript
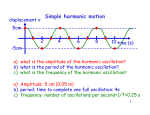
Chapter 11 Assignment KEY Simple Harmonic Motion 1. Define the following terms: • Periodic motion - the motion of an object in a repeated pattern over regular time intervals • Simple harmonic motion - a periodic motion generated by a linear restoring force • Linear restoring force – a force obeys F = -kx, where F is the restoring force, x is the position measured with respect to the resting position, and k is a constant. The minus sign shows that the force is a restoring force, tending to move the object back toward its resting position. "Linear" means that the force required to hold the object a distance x from its equilibrium point is linearly proportional to the distance x, with k the constant of proportionality. 2. Is the acceleration of a simple harmonic oscillator ever zero? If so, where? Explain. The acceleration of a simple harmonic oscillator is zero whenever the oscillating object is at the equilibrium position. Here, there is no displacement, thus restoring force is zero and the 2nd law of motion states that acceleration must be zero. 3. Is the motion of a piston in an automobile engine simple harmonic motion? Explain. The motion of the piston can be approximated as simple harmonic. First of all, the piston will have a constant period while the engine is running at a constant speed. The speed of the piston will be zero at the extremes of its motion – the top and bottom of the stroke – which is the same as in simple harmonic motion. There is a large force exerted on the piston at one extreme of its motion – the combustion of the fuel mixture – and simple harmonic motion has the largest force at the extremes of the motion. Also, as the crankshaft moves in a circle, its component of motion in one dimension is transferred to the piston. 4. How would you double the maximum speed of a simple harmonic oscillator? Since the real spring has mass, the mass that is moving is greater than the 1 k , a larger mass means a mass at the end of the spring. Since f = 2π m smaller frequency. Thus the true frequency will be smaller than the ‘massless spring’ approximation. And since the true frequency is smaller, the true period will be larger than the “massless spring” approximation. About 1/3 the mass of the spring contributes to the total mass value. 5. Does a car bounce on its springs faster when it is empty or when it is fully loaded? Explain. The period of oscillation is T = 2π m so fully loaded means large m, so larger k T, so it bounces slower. 6. If a pendulum clock is accurate at sea level, will it gain or lose time when taken to high altitude? The period of a pendulum clock is inversely proportional to the square root of l g, T = 2π . When taken to high altitude, the value of g will decrease (by a g small amount), which means the period will increase. If the period is too long, the clock is running slow and so will lose time. 7. A tire swing hangs from a branch nearly to the ground. How could you estimate the height of the branch using only a stopwatch? The tire swing approximates a simple pendulum. With a stopwatch, you can gT 2 for the length. measure the period T of the tire swing, and then solve l = 4π 2 8. When a 65-kg person climbs into a 1.00 x 103-kg car, the car’s springs compress vertically by 2.8 cm. What will be the frequency of vibration when the car hits a bump? We find the spring constant from the compression caused by the increased weight: k = mg/x = (65 kg)(9.80 m/s2)/(0.028 m) = 2.28 × 104 N/m. The frequency of vibration will be: f = 1 2π k 1 = m 2π 2.28 × 10 4 N/m = 0.74 Hz 1065 kg 9. An elastic cord is 65 cm long when a weight of 55 N hangs from it and is 85 cm long when a weight of 80.0 N had from it. What is the spring constant of the elastic cord? We find the spring constant from the elongation caused by the increased weight: k = ∆mg/∆x = (80 N – 55 N)/(0.85 m – 0.65 m) = 1.3 × 102 N/m. 10. A small fly of mass 0.15 g is caught in a spider’s web. The web vibrates predominately with a frequency of 4.0 Hz. (a) What is the value of the effective spring constant for the web? (b) At what frequency would you expect the web to vibrate if an insect of mass 0.50 g were trapped? (a) We find the effective spring constant from the frequency: 1 k f = 2π m k = 4π 2 f 2 m = 4π 2 ( 4.0 Hz) 2 (0.00015 kg) k = 0.0947 N/m (b) The new frequency of vibration will be: 1 k 1 0.0947 N/m f = = = 2.19 Hz 2π m 2π 0.0005 kg 11. If a pendulum makes 36 vibrations is 50.0 s, what is its (a) period and (b) frequency? (a) We find the period from the time for N oscillations: T = t/N = (50 s)/36 = 1.4 s. (b) The frequency is f = 1/T = 1/(1.39 s) = 0.72 Hz. 12. You want to build a grandfather clock with a pendulum that has one second between its ‘tick’ (swinging to) and its ‘tock’ (swinging fro). (a) How long do you make the cable on the pendulum? (b) Suppose the cable stretches a bit from the weight on the end. Will the clock run fast or slow? (a) Because the period includes one “tick” and one “tock”, the period is two seconds. We find the length from: T = 2π l= l g gT 2 (9.81 m/s 2 )(2.00 s) 2 = = 0.994 m 4π 2 4π 2 (b) We see that an increase in L will cause an increase in T. This means that there will be fewer swings each hour, so the clock will run slow. 13. What is the period of a simple pendulum 50.0 cm long (a) on Earth, (b) on the Moon and (c) when it is in a freely falling elevator? (a) For the period on Earth we have l (0.5 m) T = 2π = 2π = 1.42 s g 9.81 m/s 2 (b) In a freely falling elevator, the effective g is zero, so the period would be infinite (no swing). 14. The length of a simple pendulum is 0.66 m, the pendulum bob has a mass of 310 g, and it is released at an angle of 12.0o to the vertical. (a) With what frequency does it vibrate? Assume SHM. (b) What is the pendulum bob’s speed when it passes through the lowest point of the swing? (c) What is the total energy stored in this oscillation, assuming no losses to friction? (a) For the frequency, we have: f = 1 2π g 1 = 2π l 9.81 m/s 2 = 0.614 Hz 0.66 m (b) We use the law of conservation of energy between the release point and the lowest point: E kinitial + E pinitial = E k final + E p final 0 + mghi = 1 2 mv f + 0 2 ∴ v f = 2 ghi = 2(9.81 m/s 2 )(0.66 m) (1 − cos 12 o ) = 0.53 m/s (c) The energy stored in the oscillation is the initial potential energy: Epi = mgh = (0.310 kg)(9.80 m/s2)(0.66 m)(1 – cos12°) = 0.044 J