Download Accretion

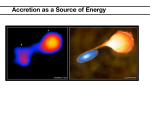
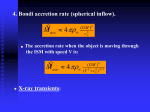
Accretion
High Energy Astrophysics
[email protected]
http://www.mssl.ucl.ac.uk/
2. Accretion: Accretion by compact objects;
Eddington luminosity limit; Emission
from black holes and neutron stars; X-ray
binary systems – Roche lobe overflow and
stellar wind accretion
[3]
2
Introduction
• Mechanisms for high energy radiation
X-ray sources
Supernova remnants
Pulsars
thermal
synchrotron
loss of rotational energy
magnetic dipole
3
Accretion onto a compact object
• Principal mechanism for producing highenergy radiation
• Most efficient method for energy production
known in the Universe
Eacc
Mm
G
R
Gravitational potential
energy released for
body of mass M and
radius R when mass m
is accreted
4
Example - neutron star
Accreting mass m = 1kg onto a neutron star:
m
neutron star mass = 1 M
R = 10 km
R
16
=> ~ 10 m Joules,
16
i.e. approx 10 Joules per kg of M
accreted matter - as electromagnetic radiation
5
Efficiency of accretion
• Compare this to nuclear fusion
H => He releases ~ 0.007 mc2
~ 6 x 1014 m Joules - 20x smaller
Eacc
Mm
G
R
Energy released is proportional
to M/R i.e. the more compact a
body, the more efficient
accretion will be
6
Accretion onto white dwarfs
• For white dwarfs, M~1 solar mass and
R~10,000km so nuclear burning more efficient
by factor of ~50
• Accretion still an important process however:
- nuclear burning on surface => nova outburst
- accretion important for much of lifetime
7
Origin of accreted matter
• Given M/R, luminosity produced depends on
.
accretion rate, m
.
Lacc
dEacc GM dm GMm



dt
R dt
R
• Where does accreted matter come from?
ISM?
No – captured mass too small.
Companion
Star?
Yes
8
Accretion onto AGN
• Active Galactic Nuclei, M ~ 109 M
- very compact, very efficient (cf nuclear)
- accretes surrounding gas and stars
9
Fuelling a neutron star
• Mass = 1 M
31
observed luminosity = 10 J/s (in X-rays)
• Accretion produces ~ 1016 J/kg
.
31
16
• m = 10 / 10 kg/s
~ 10-8 M/year
22
~ 3 x 10 kg/year
10
The Eddington Luminosity
• There is a limit to the luminosity that can be
produced by a given object, known as the
Eddington luminosity.
• Effectively this is when the inward
gravitational force on matter is balanced by
the outward transfer of momentum by
radiation.
11
Eddington Luminosity
M
r
m
Fgrav Frad
Mm
Fgrav  G 2 Newton
r
Accretion rate
controlled by
momentum transferred
from radiation to mass
Note: R << r
Outgoing photons from M scatter off accreting
material (electrons and protons).
12
Scattering
L = accretion luminosity
no. photons
crossing at r
per second
L 1

4r 2 h
photons m -2 s -1
Scattering cross-section will be Thomson
cross-section se ; so no. scatterings per sec:
Ls e
4r 2 h
13
Momentum transferred from photon to
particle:
h
h
e-, p
c
Momentum gained by particle per second
= force exerted by photons on particles
Ls e h
Ls e

Newton
2
2
4r h c
4r c
14
Eddington Limit
radiation pressure = gravitational pull
At this point accretion stops, effectively
imposing a ‘limit’ on the luminosity of a
Ls e
Mm
given body.
G 2
2
4r c
r
So the Eddington
luminosity is:
L
4cGMm
se
15
Assumptions made
• Accretion flow steady + spherically
symmetric: e.g. in supernovae, LEdd
exceeded by many orders of magnitude.
• Material fully ionized and mostly
hydrogen: heavies cause problems and may
reduce ionized fraction - but OK for X-ray
sources
16
What should we use for m?
Electrostatic forces between e- and p binds
them so they act as a pair.
Thus: m  m p  me  m p


4 3 108 6.67 1011.1.67 1027
LEdd 
M Joule/sec
 29
6.65 10

31  M
 Joule/sec
 6.3 M Joule/sec  1.3 10 
 M SUN 
17
Black Holes
• Black hole does not have hard surface - so what do
we use for R?
• Use efficiency parameter, h and
• 2
Lacc  hMc
at a maximum h = 0.42, typically h = 0.1
• Solar mass BH ~ as efficient as neutron star
• From a classical viewpoint, the escape velocity from
a star of mass m and radius r is v = (2GM/r)1/2 so
for v = c, rg = 2GM/c2 – the Schwarzschild radius
which is also a measure of BH “surface”
18
Emitted Spectrum
• Define temperature Trad such that h ~ kTrad
• Define ‘effective’ BB temp Tb

Tb  Lacc / 4R s
2

1/ 4
• Thermal temperature, Tth such that:
M mp  me 
3
G
 2 kTth => Tth 
R
2
GMmp
3kR
19
Accretion temperatures
• Flow optically-thick:
Trad ~ Tb
• Flow optically-thin:
Trad ~ Tth
20
Accretion energies
• In general,
Tb  Trad  Tth
• For a neutron star,
assuming
Lacc  LEdd
Tth  5.4 10 K
7
Tb  210 K
11
 M 
 J / s
 1.3 10 
 M Sun 
31
21
Neutron star spectrum
• Thus expect photon energies in range:
1keV  h  50MeV
• Similarly for a stellar mass black hole
26
6
• For white dwarf, L acc~ 10 J/s, M ~ M, R = 5x10 m,
6eV  h  100keV
• => optical, UV, X-ray sources
22
Accretion modes in binaries
For binary systems which contain a compact
star, either white dwarf, neutron star or black
hole, mechanisms are:
(1) Roche Lobe overflow
(2) Stellar wind
-
corresponding to different types of X-ray
binary
23
Roche Lobe Overflow
• Compact star M1 , normal star M 2 with M2 > M1
M2
CM
M1
+
a
• Normal star expanded or binary separation
decreased => normal star feeds compact star
24
Roche Equipotentials
Sections in
the orbital
plane
M1
M2
+ +
CM
+
v
L1
M 2  M1
25
Accretion disk formation
Matter circulates around the compact object:
AM increases
outwards
matter
inwards
26
• Material transferred has high angular
momentum so must lose it before accreting
=> disk forms
• Gas loses angular momentum through
collisions, shocks, viscosity and magnetic
fields: kinetic energy converted into heat
and radiated.
• Matter sinks deeper into gravity of compact
object
27
Accretion Disk Luminosity
• For most accretion disks, total mass of gas in the disk
is << M so we may neglect self-gravity
• Hence the disk material is in circular Keplerian orbits
with angular velocity WK = (GM/R3)1/2 = v/R
• Energy of particle with mass m in the Kepler orbit of
radius R just grazing the compact object is
1
2
1
mv2 = 12 m GM
=
E
R
2 acc
• Gas particles start at large distances with negligible
energy, thus
Ldisk =
.
Mm
G 2R
=
1
2 L acc
28
Disk structure
The other half of the accretion luminosity is
released very close to the star.
X-ray
Hot, optically-thin
inner region; emits
bremsstrahlung
UV optical
bulge
Outer regions are cool,
optically-thick and emit
blackbody radiation
29
Magnetic neutron stars
For a neutron star with a strong magnetic field,
disk is disrupted in inner parts.
Material is
channeled
along field lines
and falls onto
star at magnetic
poles
This is where most radiation is produced.
Compact object spinning => X-ray pulsator
30
‘Spin-up pulsars’
• Primary accretes material with angular
momentum => primary spins-up (rather
than spin-down as observed in pulsars)
• Rate of spin-up consistent with neutron star
primary (white dwarf would be slower)
• Cen X-3 ‘classical’ X-ray pulsator
31
Stellar Wind Model
Early-type stars have intense and highly
-5
-6
supersonic winds. Mass loss rates - 10 to 10
solar masses per year.
For compact star - early star binary, compact
star accretes if
GMm
1 m(v 2 + v 2 )
>
w
ns
r
2
32
Thus:
r acc = 2GM
2 + v2
vw
ns
Radial Wind Vel
vw
r acc
Neutron Star
Orbital Vel vns
bow shock
matter collects in wake
33
Stellar wind model cont.
• Process much less efficient than Roche lobe
overflow, but mass loss rates high enough to
explain observed luminosities.
-8
• 10 solar masses per year is required to produce
X-ray luminosities of 10 31J/s.
• 10-5 – 10-6 solar masses per year available from
early-type stellar winds
34
ACCRETION
END OF TOPIC
35
Accretion Disk Luminosity
For an accretion disk with inner radius R, KE = T and
PE = U:
2T + U = 0 from the Virial theorem
hence
T=-½U
but
U = - GMm/R
for an infalling particle of mass m
and so
T = ½ GMm/R
if
E = T + U is total energy
then
E = ½ U = - ½ GMm/R
or
Luminosity = - ½ (GM/R) dm/dt
36
Eddington Limit
radiation pressure = gravitational pull
At this point accretion stops, effectively
imposing a ‘limit’ on the luminosity of a
Ls e
Mm
given body.
G 2
2
4r c
r
So the Eddington
luminosity is:

4cGMm
se
37
Types of X-ray Binaries
Group I
Luminous (early,
massive opt countpart)
(high-mass systems)
hard X-ray spectra
(T>100 million K)
often pulsating
X-ray eclipses
Galactic plane
Population I
Group II
Optically faint (blue)
opt counterpart
(low-mass systems)
soft X-ray spectra
(T~30-80 million K)
non-pulsating
no X-ray eclipses
Gal. Centre + bulge
older, population II
38