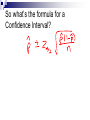Download Point Estimates

Point Estimates
Remember…..

Population
 It

is the set of all objects being studied
Sample
 It
is a subset of the population
Parameter

Quantity computed from values in a
population
 Usually


p
not known
Statistic

Quantity computed from values in a
sample.
 Computed
x
s
p
directly from sample data
Point Estimate

It is a single number that is based on
sample data that represents a plausible
value of the characteristic for the
population.

It’s the statistic (from a sample) that we
use to estimate the parameter (of the
population).
Examples

To find a point estimate of the average height of
students in this class I could use a sample of 10
people and find their average height.

To find the percent of green M&M’s in a bag, I
could use 20 bags and find the average percent
in those bags to estimate the true population
proportion.
An article on affirmative action reported that 537 of
the 1013 people surveyed believed that affirmative
action programs should be continued. Find a point
estimate of the population proportion.

Calories per ½ cup serving for 16 popular chocolate ice
cream is shown below. Find a point estimate for the
number of calories in a serving of chocolate ice cream.
270
170
160
160
199
160
150
180
150
140
160
290
190
170
110
170
Calories per ½ cup serving for 16 popular chocolate ice
cream is shown below. Find a point estimate for the
number of calories in a serving of chocolate ice cream.
We could use the
270
170
160
160
199
160
150
180
150
140
160
290
190
170
110
170
mean:
median:
Calories per ½ cup serving for 16 popular chocolate ice
cream is shown below. Find a point estimate for the
proportion that are greater than 190.
270
170
160
160
199
160
150
180
150
140
160
290
190
170
110
170
We tend to pick an estimate that
yields an accurate estimate.

To estimate a proportion – we use a proportion
(not a mean).

To estimate how many – we use the mean,
median, or trimmed mean

To estimate variation – we use standard
deviation, variance, or range
For our class (the population),
find a point estimate for the …

Average height

Difference between height of girls & height
of the boys

Proportion with brown eyes
Unbiased Statistic

It’s a statistic whose mean value is equal
to the value of the population being
estimated.

Biased – not equal to the population being
estimated.
Examples of unbiased
estimators

mean: x
median
trimmed mean


Proportion:
Variance:
s2
x  x



n 1
2

x
2
x



n 1
n
2
Biased: Range

If using a sample – it will only equal the
population if you have the lowest & highest
values. The probability for this to happen
is very small – almost 0.

Thus it’s biased because for most, the
sample range is smaller than the
population range.
Airborne Times: 57, 54, 55, 51, 56, 48, 52,
51, 59, 59. Find point estimate of mean &
variance.
Put them in list 1
 Do 1-var Stat
 To get the variance, you must take the st.
dev. (Sx) and square it.

Confidence Interval
Proportions
Remember

Point estimate is different every time since
it depends on the sample selected.

In choosing a confidence interval, it is not
a single point but rather an interval of
reasonable values.
Confidence Interval

Interval of reasonable values for the
characteristic chosen with a degree of
confidence.

The value of the population characteristic
will likely be between the upper and lower
bounds.
Confidence Level

This represents the success rate of the
method used to construct the interval.

If I repeat the process over & over,
approximately this % of the intervals will
contain the true parameter.
Remember – for sampling
distributions of proportions….

np  5

nq  5
So, if I want to be 95% confident that my interval contains
the true proportion, how many deviations would I be from
the mean proportion?
So what’s the critical z value that
corresponds to a 98% confidence.
So what’s the formula for a
Confidence Interval?
PANIC!
P – Parameter (tell what we are estimating)
 A – Assumptions
 N – Name the Formula
 I – Interval (calculate it)
 C - Conclusion

When 320 college students were surveyed, 125 said they own their car.
Construct a 90% confidence interval for the proportion of college
students who own their car.
A survey of 100 fatal accidents showed that 52 were alcohol related.
Construct a 98% confidence interval for the proportion of fatal accidents
that were alcohol related.
Explain what the 90% confidence
level means.
If I repeat this process over & over, 90%
of the intervals found will contain the
true population proportion of
households that own at least one gun.
What happens to the width of the interval if
we go from 90% confidence to 98%
confidence?
What happens to the width of the interval is
we increase the sample size?
Homework

Worksheet