* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download MDI: Trapped modes and other power losses
Survey
Document related concepts
Transcript
MDI: Trapped modes and other power losses
Alexander Novokhatski, Eleonora Belli, Miguel Gil Costa
Michael K. Sullivan and Roberto Kersevan
CERN and SLAC National Accelerator Laboratory
FCC week 2017
May 31, 2017, Berlin
A. Novokhatski 5/31/17
1
Outline
I.
II.
III.
IV.
V.
VI.
VII.
Why do we need to pay attention to the shape of the Interaction
Region beam pipe?
An unavoidable trapped mode
Possible smooth pipe connections
Status of the trapped mode analyses
A proposal to use a HOM absorber
Prediction for IR HOMs heating
Conclusion and future steps
A. Novokhatski 5/31/17
2
Why do we need to pay attention to the shape of
the IR beam pipe?
•
•
•
•
In terms of collective effects, the dominant issue is the relatively high beam current
(1.45 A) that must be supported in each ring of the electron-positron FCC for Zproduction.
A beam circulating in a storage ring interacts with its surroundings
electromagnetically by inducing image currents in the walls of the vacuum chamber
and exciting Higher Order Modes in the chamber elements, such as RF cavities,
kickers, vacuum valves, collimators, bellows, BPM electrodes and the Interaction
Region.
Beam pipes of two rings are combined into one pipe in the IR.
Because of the complicated IR geometry a lot of electromagnetic power can be
radiated. Some part of radiation will propagated out of the IR, but some may stay
inside in the form of trapped wake fields.
A. Novokhatski 5/31/17
3
Main HOMs effects in IR (all are negative)
• The frequency of some HOMs can be in a resonance with a harmonic of the revolution
frequency and the amplitude will grow exponentially and can reach a high value.
• In practice this happens often.
• Heating of the beam pipe walls
•
•
•
•
Temperature and vacuum rise
Decreasing the pumping speed due to the large temperature rise
Pipe deformations and vacuum leaks
Melting of thin shielded fingers
• Breakdowns and multipacting
• Vacuum spikes
• Beam aborts
• Electromagnetic waves can go outside vacuum chamber through pump high voltage
electrodes
• Interaction with sensitive detector electronics
• All effects lead to increasing the background or unstable operation.
• Examples from the PEP-II operation can be found in NIM A 735(2014)349–365
A. Novokhatski 5/31/17
4
An unavoidable trapped mode
•
•
Trying to find an optimum geometry for IR with minimum electromagnetic wave
excitation (minimum impedance), we discovered one mode, which stays even in a
very smooth geometry.
First calculations were done using a flat version of the code NOVO for a flat
geometry of IR. This mode is situated near the connection of the two pipes.
Metal walls
electric field lines
Pipe
connection
beam
+
+
A surface current has
also a longitudinal slope
beam
Metal walls
•
This mode has a longitudinal electrical component and can be easily excited by
electron and positron beams.
A. Novokhatski 5/31/17
5
Possible smooth pipe connections
•
•
Among other configurations for the geometry of the IR beam pipe, which has the smallest
impedance, we considered three different models of IR with the same diameter of incoming
pipes and of a central pipe – 30 mm in a diameter.
1. The incoming pipes are smoothly squeezed to the half circle shape in order to merge
into the central pipe with a constant diameter.
2. The incoming pipes near the connection are circular pipes. The central part near the
pipe connection has a transition to an approximately elliptical shape of a double size in
the horizontal direction. The connection of two pipes and the elliptical shape contains
some small sharp transitions.
3. Each pipe near the connection has a transition to a half of a special shape determined
by the shape of the transition from the central pipe (a proposal from Oide Katsunobu). A
full smooth geometry.
We will show details of these models and make a comparison between the smoothed
geometries 1 and 3.
A. Novokhatski 5/31/17
6
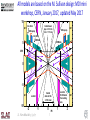
All models are based on the M. Sullivan design: MDI mini
workshop, CERN, January 2017, updated May 2017
10
QC1
Central beam
pipe +/-12.5 cm
in Z. r = 15 mm
2 cm thick
NEG pump
NEG pump
QC1
1 cm thick
HOM Abs
5
HOM Abs
Be
Cu
cm
Cu
0
-5
QC1
-10
LumiCal
-2
A. Novokhatski 5/31/17
LumiCal
50-100 mrad
from exiting
axis
Central
detector SA
+/-150 mrad
-1
0
m
7
1
2
QC1
Current status of the HOMs analyses
• Eleonora Belli did a tremendous work for electromagnetic
calculations in Interaction Region.
• We calculate wake potentials of a 4m long main part of the IR.
• Initially we designed the IR model using the CST code editor, but we
had a problem with the mesh distribution for a smooth IR geometry.
• As this was an important point we decided to use CAD files as an
input file for CST and HFSS codes.
• We got a support and professional files from Miguel Gil Costa.
• New approach for the wake field and eigen mode simulation using
CAD files from “CATIA” for Interaction Region.
• Established the file format and additional file description for better
communication between “CATIA” and “CST”.
A. Novokhatski 5/31/17
8
Model 1. Squeezed incoming pipes.
A. Novokhatski 5/31/17
9
We found one trapped mode
30 mm
Electric field line distribution
Same field structure as for the unavoidable mode
A. Novokhatski 5/31/17
10
Wake potential and spectrum
Wake potential describes the integrated effect
of the wake
¥
fields along the beam trajectory W(t ) = E (t, z)
dt
f=5.78 GHz
ò
-¥
A note: a positive value of the real part of the wake field spectrum shows a good quality
of the calculation of the wake potential.
A. Novokhatski 5/31/17
11
z
z=c(t-t )
Model 2. Small sharp transition.
We found also one trapped mode at 5.67 GHz.
A. Novokhatski 5/31/17
12
Model 3. Transitions design. Miguel Gil Costa
General view
Central round pipe 30 mm
Transition from round to an “ellipse”
Transition of incoming circular pipes 30 mm to half of an “ellipse”
A. Novokhatski 5/31/17
13
All smooth geometrical transitions.
A. Novokhatski 5/31/17
14
Inner view
A. Novokhatski 5/31/17
15
We also found one mode, but less frequency
3.46 GHz
Model 3
A. Novokhatski 5/31/17
16
Loss frequency integral calculated from the
spectrum of wake potential of a 2.5 mm bunch
0.3
0.08
Model 3
0.07
0.25
loss fequency integral
0.2
0.05
0.15
0.04
0.03
0.1
loss integral
realW
0.02
0.05
0.01
0
0
0
2
4
6
8
10
12
14
frequency [GHz]
A. Novokhatski 5/31/17
17
16
18
20
Re{W}
0.06
A trapped mode. Same field structure.
65 mm
electric field lines
A. Novokhatski 5/31/17
18
The structure of the mode field distribution shows how we
can capture it with minimum disruption of the image
currents of the beam field.
Electric field lines in
this place are
perpendicular to the
beam trajectory
A. Novokhatski 5/31/17
19
We can make longitudinal slots oriented perpendicular to the HOM
electric field, which allow the mode field to easily propagate though
these slots. At the same time, the beam field will not pass through.
Then we can put a water-cooled absorber above the slots.
A. Novokhatski 5/31/17
20
We have already found some initial positions for the slots.
cupper blocks
absorbing tiles
water pipes
slots
HOM absorber will not only absorb the mode, but also capture some propagating fields
A. Novokhatski 5/31/17
21
To calculate the radiation power we use a loss
frequency integral K () Re{ 1 W () ()d} 1 () Re{Z ()}d
2
Model 1
s
s
0
s
0
propagating mode loss factor,
depends upon the bunch length
TM 01
Pprop I 2 k kHOM b
TE11
trapped mode loss factor
PHOM 2 I 2 kHOM l ,HOM
propagating longitudinal modes
A. Novokhatski 5/31/17
propagating transverse modes can be
captured by 22
the HOM absorbers
Estimates for HOM and propagating power.
Comparison of the models
model trapped mode
close harmonics
frequency
N-
[GHz]
I
5.774
N+
frequency
14
15
mode loss
tau
trapped power loss factor of propagating
fields
propagating
power
factor
Ql=100
[V/pQ]
[nsec]
[kW]
[V/pC]
[V/pC]
[V/pC]
[kW]
[kW]
0.38
5.51
8.71
0.10
0.46
2.05
2.42
10.77
0.08
9.20
2.91
0.03
0.09
0.40
0.45
2.10
for I= 1.45 A bunch 10 mm bunch 5 mm bunch 2.5 mm bunch 5mm bunch 2.5 mm
5.6 GHz 6.0 GHz
III
3.459
8
9
3.2 GHz 3.6 GHz
PHOM 2 I 2 k HOM l , HOM
Pprop I 2 k k HOM b
Model 3 is 5 times better than model 1.
A. Novokhatski 5/31/17
23
Resistive wall wake potential
Electric field
9E-08
8E-08
7E-08
Eleonora Belli
E [V/pC/m]
6E-08
5E-08
æZ s æ æ Z s æ
E = E0 æ 0 æexp æ- 0 x2 æ
æ4p ct æ æ 4ct æ
4E-08
3E-08
2E-08
1E-08
0
0
5
10
15
20
25
30
35
Time [µsec]
conductivity
/Ohm/m
m
Al
Cu
SS
Au
Be
Ni
NEG
35000
58000
1400
48800
25000
14600
55-1000
single bunch
-4
-2
A. Novokhatski 5/31/17
0
2
4
6
8
Multi-bunch regime. Losses may
be increased several times
More information is needed about
layers of the beam pipe (Au,Be)
Current estimate is 200 W/m
distance [s/sigma]
24
Conclusion and future steps
•
•
•
We have designed a smooth geometry of the IR vacuum chamber, which has a relatively
small HOMs impedance.
Each beam of 1.45 A will produce electromagnetic power of approximately 5 KW from
both connections. This power will be mainly absorbed in the two sets of HOM absorbers.
More work will be needed to further optimize the HOM absorbers.
Beam pipe requires water or air cooling.
Need more analyses.
This optimal shape of the
IR beam pipe can be also
used in other circular
colliders (scaled if needed)
A. Novokhatski 5/31/17
25
Acknowledgement
We would like to thank Frank Zimmerman, Manuela Boscolo and
especially Michael Benedikt for their great support of this work.
We are also happy to thank Oide Katsunobu, Mauro Migliorati and
the MDI team for many useful discussions and help.
Thank you!
A. Novokhatski 5/31/17
26






























![See our full course description [DOCX 84.97KB]](http://s1.studyres.com/store/data/022878803_1-2c5aa15da187b4cc83f0e4674d9530a8-150x150.png)



