Download Slide

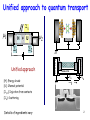
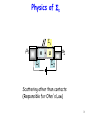
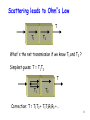
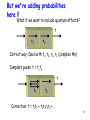
Scattering
µ1
µ2
m1
Ss
H + U
S1
Numbers (e,g,U)
Rate equations


Matrices (H, S, U)
NEGF formalism
m2
S2
1
Unified approach to quantum transport
m1
Ss
H + U
S1
m2
S2
Unified approach
[H]: Energy levels
[U]: Channel potential
S
O
U
R
C
E
D
R
A
I
N
INSULATOR
VG
VD
I
[S1,2]: Injection from contacts
[Ss]: Scattering
Details of ingredients vary
2
Physics of Ss
m1
Ss
H + U
S1
m2
S2
Scattering other than contacts
(Responsible for Ohm’s Law)
3
Phase Breaking SP
m1
Ss
H + U
S1
S2
m2
ihdy/dt – Hy – SPy = SP
Environment changes during conduction through interactions
(eg. Atoms vibrating, spins flipping, light absorption)
Many-electron theory needed
S, S function of occupancy
(Pauli exclusion)
4
E.g. Electron-phonon
m1
Ss
H + U
S1
m2
S2
Sin(E) ~ G.F = n(E-Eph) x Pabs(Eph)
+ n(E+Eph) x Pem(Eph)  We’ll revisit this later
Enforces Irreversibility
m1
Ss
H + U
S1
S2
m2
ihdy/dt – Hy – SPy = SP
Environment changes during conduction through interactions
Brings system back to equilibrium
PA->B/PB->A = exp[-(EB-EA)/kT]
Signatures of Scattering
Depending on DOS,
scattering can increase
or decrease G
Phonon assisted
Tunneling  Sidebands
7
Signatures of Scattering
g1 g 2
Electron can lose energy by setting molecule vibrating
Current picks up signatures
of these vibrations
(Inelastic Electron
Tunneling Spectroscopy)
Expt. Mark Reed (Yale)
8
Scattering leads to Ohm’s Law
T
T1
T2
What’s the net transmission if we know T1 and T2 ?
Simplest guess: T = T1T2
T
T1
T2
Correction: T = T1T2 + T1T2R1R2 + ..
9
Bottom-Up treatment of Ohm’s Law
T
T1
T2
Net result: T = T1T2 + T1T2R1R2 + T1T2(R1R2)2 + …
= T1T2/(1-R1R2)
Since R1,2 = 1 – T1,2
T = T1T2/(T1+T2-T1T2)
 1/T = 1/T1 + 1/T2 -1
10
There is an additive component !
T
TL
TL+dL
Let r = (1-T)/T = R/T
Then, r(L+dL) = r(L) + r(dL)
= r(L) + dL/L
 dr/dL = 1/L
L: Scattering length
 r(L) = L/L
The limits L  0, ∞
 T(L) = L/(L+L)
make sense
11
Bottom-Up treatment of Ohm’s Law
G = (2q2/h)MT (Landauer Theory)
R = h/2q2MT
= h/2q2M + (h/2q2M)R/T
Contact
Resistance
Intrinsic Device
Resistance
Rdevice = (h/2q2M)L/L
#modes depends on how many half wavelengths are fitted in
M = A/(lF/2)2 = AkF2/p2
In 3-D, kF3 = 3p2n, and kF = mvF/ħ = mL/tħ
Thus Rdevice = rL/A, where conductivity s = 1/r ~ nq2t/m
OHM’s LAW
12
But we’re adding probabilities
here !!
What if we want to include quantum effects?
t
t1
t2
Correct way: Deal with t1, t2, r1, r2 (complex #s)
Simplest guess: t = t1t2
t
t1
t2
Correction: t = t1t2 + t1t2r1r2 + ..
13
Including phases then…
t1
t
t2
Net result: t = t1t2/(1-r1r2)
T = |t|2 = |t1t2/(1-r1r2)|2
= T1T2/[1+R1R2-2(R1R2)cosDj]
Dj = 2kDx
• Resistances may not add !!
• Resistances may be tunable by altering phase
(e.g. path-length, temperature, magnetic field)
14
Interference with electrons
Goldman group, Stonybrook
Chandrasekhar et al, PRL ‘85
15
When do we simply add resistances?
When interferences are unimportant.
e.g. Impurities, temperature
All cosine phase terms drop out in numerator (“Dephasing”)
Ironically, we know how to solve the quantum problem!!
So how would the classical equations come out of NEGF?
(Dephasing or Incoherence)
16
Simple Model for Scattering
‘s’
m1
Ss
H + U
S1
S2
m2
Think of scattering center as
a ‘virtual’ contact in equilibrium
that extracts and reinjects
charge after randomizing its
phase
T12 = [g1g2/(g1+g2)]D(E)
T1s = [g1gs/(g1+gs)]D(E)
Ts2 = [gsg2/(gs+g2)]D(E)
Property of regular contacts: In thermal equilibrium
determined by f1,2
17
Buttiker Probe
Is =
dE

+.T2s(E) (f2 - fs ) = 0
‘s’
m1
Ss
H + U
S1
T1s(E) (f1 - fs )
S2
Solve for fs and
calculate
m2
I1 =
dE

T1s(E) (f1 - fs )
+.T12(E) (f1 - f2 )
18
Elastic Scattering
Elastic scattering
(No energy exchange)
Set integrand of Is = 0
‘s’
Ss
m1
H + U
S1
S2
1/T1s
1/Ts
2
1/T1
2
m2
fs = (T1sf1+Ts2f2)/(T1s+Ts2)
I1 =
dE T(E) (f1

- f2 )
T = T12 + T1sTs2/(T1s+Ts2)
Like resistor network!
19
Inelastic Scattering
‘s’
m1
Ss
H + U
S1
m2
S2
Many parallel ‘channels’
Scattering exchanges
energy among them
(‘Vertical Flow’)
A lot of energy exchange
(‘Thermalization’)
fs(E) = 1/[1+exp(E-ms)/kT]
Adjust ms for zero Is
Here we assume all
energy relaxation
processes allowed
A single vibration (phonon)
can only cause change in
energy of ħw0
20
Beyond Buttiker Probes
Instead of gs assume Ss has some energy structure
More importantly, can’t calculate transmission
between scatterer and channel very easily
T1s ≠Tr(g1GgsG+), since Ssin ≠ gsfs
Use instead
I1 =
2q

dETr[S1inA-G1Gn]
h
21
Self-energy for Interacting systems
El-El
S(E): complicated function
of f
Instead of
G(E) = 2p|t|2D(E)
Coulomb Blockade
Kondo effect
We get
G(E) = 2p|t|2f(E)D(E)
22
Self-energy for dephasing scattering
Vibrations/Spins
(“Bosons”)
Ss = hGh+
Ssin(E) = D[Gn(E-ħw)Nw+ Gn(E+ħw)(Nw+1)] for 1 mode (Slide 5)
ħw
E
E-ħw
Phonon Absorption
E
ħw
E+ħw
Phonon Emission
Ssout(E) = D[Gp(E-ħw)Nw + Gp(E+ħw)(Nw+1)]
23
Self-energy for dephasing scattering
Vibrations/Spins
(“Bosons”)
Gn = GSsinG+
Ss = hGh+
Phonon emission
Gs = Ssin + Ssout
Ss = H(Gs)
Polaronic shift
Phonon absorption
24
Going beyond self-energy
‘s’
m1
Ss
H + U
S1
m2
S2
Beyond a certain point,
calculating S(E) becomes
hard, and may need summation
of various infinite (possibly)
non-convergent series
A more accurate way is to
directly solve the transport
problem in ‘Fock’ space like
in chapter 3
25
Summary
Classical equations come out of quantum if we
lose phase information (‘memory’) through dephasing
While the consequence of dephasing is simple to implement
(Newton’s Laws!), it’s not easy to get out of NEGF, especially
if we have intermediate degrees of dephasing (ie, some
incoherence, but not enough to make it classical)
Needs careful physical considerations, but could have really
important roles to play (e.g. spectroscopy)
26