Download Vocabulary - Hartland High School

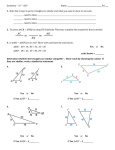
Section 6.5 Prove Triangles Similar by SSS and SAS
Goal  Use the SSS and SAS Similarity Theorems.
Theorem 6.2: Side-Side-Side (SSS) Similarity Theorem
If the corresponding side lengths of two triangles are PROPORTIONAL, then the triangles
are similar.
If
AB BC CA


, then ABC  RST
RS
ST TR
Example 1: Is either DEF or GHJ similar to ABC?
Compare ABC and DEF by finding ratios of corresponding side lengths.
Compare ABC and GHJ by finding ratios of corresponding side lengths.
Example 2: Find the value of x that makes ABC ~ DEF.
Checkpoint:
1. Find the value of x that makes ∆ABC ~ ∆DEF.
Section 6.5 Prove Triangles Similar by SSS and SAS
Theorem 6.3: Side-Angle-Side (SAS) Similarity Theorem
If an angle of one triangle is congruent to an angle of a second triangle and the lengths of the
sides including these angles are PROPORTIONAL, then the triangles are similar.
If X  M, and
ZX
XY

, then XYZ  MNP.
PM MN
Example 3: Find the value of x that makes ∆POR ~ ∆TUV
Example 4: Tell what method you would use to show that the triangles are similar.
Checkpoint
2. Find the value of x that makes the
triangles similar.
3. Explain how to show JKL ~ LKM.