Download On Constrained Optimization Approach to Object

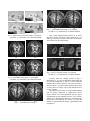
On Constrained Optimization Approach To Object Segmentation
CHIA HAN, XUN WANG, FENG GAO, ZHIGANG PENG, XIAOKUN LI, LEI HE, WILLIAM WEE
Department of Electrical & Computer Engineering and Computer Science
University of Cincinnati
Cincinnati, OH 45221-0030
USA
Abstract: - A general contour constrained optimization approach is formulated to extract a target contour in an
image for various applications. These different approaches of mean field annealing method, variational
method, and evolutionary strategy are derived to provide global and local optimal solutions using level set
numerical implementations. Impositions of constraints to characterize the contour interior features are
employed on different specific applications. Contour shape models using either the thin plate spline matching
method or the implicit polynomial representation method can be added into the optimization process to
further improve contour extraction results. A set of illustrative examples for the applications of the
approaches on biomedical images are presented.
Key-Words: - Image Segmentation, Deformable Contour Methods, Constrained Optimization.
1 Introduction
Intelligent systems with any visual ability for object
understanding need to both possess object
recognition capability at the high level of
abstraction and provide flexible and robust
capability to extract corresponding meaningful
contours or surfaces of the object of interest at the
low level of image processing. A major research
activity in our Artificial Intelligence and Computer
Vision Laboratory at the University of Cincinnati
has been to solve image-based object understanding
problems by using a framework that is built on
Deformable Contour Methods (DCM) with a
constrained energy minimization formulation of
contour extraction [1][2][3][4][5][6].
Object understanding encompasses a wide
gamma of concepts and processing methodologies
in computer vision and pattern recognition, which
may include object recognition, object interior
structure description, object motion tracking and
dynamic behavior of its parts, and visible surface
recognition with occlusion due to multiple parts. All
the processing are possible when starting with a
successful search for a good object surface or
contour delineating the target object in the image.
From the traditional 2-D image processing point
of view, given that each object has an isolatable and
discernable boundary, contour extraction simply
consists of the segmentation step in image
processing, which is to partition an image into
regions corresponding to the areas of interest and to
extract their boundary accurately. The extracted
contour is then used in subsequent operations to
provide vital information for obtaining quantitative
measurements such as area or volume, and for
determining qualitative features for latter stage of
multi-modality image registration, classification and
interpretation. Thus, contour extraction, when
considered in a broader context, becomes the
essential step in object understanding. Not only
does it form the basis of segmentation, i.e., the
isolation of the object from the background, but also
contains the ability to represent the characteristics
needed for object recognition and labeling. When a
framework that allows the integration of the latter
capability of recognition within the process of
abstracting the desired contour, then it forms the
core of the object understanding.
In this paper we will present such a framework,
which is built upon the contour energy
minimization formulation. It allows that the
knowledge of understanding the object be
represented in terms of the features and dynamic
behavior of its constituent parts of interest and be
expressed as constraints of its optimization index.
But before we get to this point, we should review
the basics of segmentation.
The problem of image segmentation, especially
extracting from images the structures that are found
in nature, is by no means trivial. For instance, in
biomedical images, there are many difficult
challenges that are well known to the image
processing research community. They include
complex
shape,
inhomogeneous
brightness
distribution both at the interior of the region of
interest and along the boundary region, very blur
contour segments, and gaps (missing edges, e.g.,
due to drop of imaging signal during acquisition).
Instances of such difficulties can be seen in the
sample images, shown in Figure 1, of different
subjects and from various imaging techniques: brain
MRI images have complex shapes with
inhomogeneous brightness distributions in both the
interior and along the contour of the gray and white
matters; and ultrasound heart images are rather
noisy with fuzzy boundary and gaps in many
portions of the contour. It is clear from these
pictures that an image-based system with the
capability for an automatic and robust segmentation
and accurate contour extraction would make a great
impact in delivering the critical functionalities of
diagnosis, treatment, and surgery planning in the
clinical applications and generating useful digital
anatomical atlas from sources, such as Visible
Human Project [7] in both clinical and educational
applications.
Fig. 1 Sample biomedical images.
These hard image segmentation problems are
not easily handled by the existing schemes, which
are primarily boundary (edge)-based and regionbased segmentation methods. The edge-based
approach is conceptually sound and there are many
edge extraction methods to choose from. However,
it has the contour linking problem when there are
either too many edge points or too few edge points
with gaps. The region-based approach is based on
the region growing methods. There are also many
similarity or dissimilarity functions to select from.
But the same problems of contour linking, disjoint
regions, and inhomogeneous intensity distribution
plague this approach as well.
A more elaborated and sophisticated approach
has also been developed in the last decade. This is
the deformable (also known as active or evolving)
contour approach [8]. This approach includes the
snakes [8][9][10][11], level sets [12][13][14][15],
and non-deterministic methods [16][17][18], and
thereafter will be referred to as deformable contour
methods (DCMs). The methods in this category
have less of the contour linking problems as they
make use of the notion of closed contour. Thus, an
interior/exterior structure could be established and a
global energy minimization function for global
control over local variation could be formulated.
The reasoning behind these methods also conforms
to the natural notion of the life dynamic evolution
process.
This evolutionary process always emanating
from the interior, as applied to image segmentation,
would provide an invaluable insight in
distinguishing the connected segments. For
instance, if many seeds grow into many plants, any
leaf in dense foliage can still be traced to its own
stem, even when the connection to its origin may be
obscured by other leaves or complex local
structures. The reverse tracking is also true; given
the right stem is selected at the beginning, following
the connection would lead to the desired leaf. But at
the present time, any of the DCMs, when applied
indiscriminately, have difficulty searching for the
global minimum contour from an arbitrary interior
point. It also has difficulty with gaps and very blur
contour segments, complex shape, inhomogeneous
interior, and lastly, it may be sensitive to the initial
location. However, most of these difficulties can be
overcome, provided that we have the understanding
of their presence and know how to tackle them
properly once they appear.
The segmentation problem would become one
of the image understanding (IU) problems and the
many techniques used in IU could be applied. When
each of the methods in the above major approaches
faces some of the aforementioned difficulties and
fails, special measure based on the knowledge of
the problem domain is usually needed to tackle
specific failures: additional image dependent pre
and
post
processing,
major
algorithmic
reformulation, and even the semi-automatic
approach with a direct human intervention are
generally introduced in attempt to overcome the
problems. However, we should note that this
approach normally involves distinct methods and
processes that are applied separately; what is
needed is a more integrated approach that offers
robustness necessary to automatically handle the
typical difficulties by keeping the strength while
avoiding the shortcomings of the existing methods.
2 Problem Formulation
The contour searching and extraction from an image
using a deformable contour strategy can be
formulated as a constrained optimization problem as
follows:
Let  be an open domain subset of  2 and
I ( x, y ) :    be the image intensity function. Our
problem is to find a close contour C ( q, t ) enclosing
region c(t) at time t, such that the contour energy
(1)
E (C (q, t ))  g ( I (C (q, t )) )ds

C
is the minimum under the constraint D( x, y )  TV
for all ( x, y)  C (t ) , where 0  TV is a constant,
s is the arc length, q is the contour parameter, and
I ( x, y ) is the image brightness at ( x, y ) . Also,
1
.
(2)
g ( I (C (q, t )) ) 
2
1  I (C (q, t ))
I (C (q, t )) is the gradient of I ( x, y ) with ( x, y )
on C ( q, t ) .
The D( x, y ) in the constraint includes any
contour interior brightness characterization features,
such as smoothness, texture, and other structural
features. Contour shape matching and fittings
specifications can be added to the contour energy.
2.1 Interior characterization constraint
We may consider any positive interior characteristic
function as a modeling function of the interior
region with D(x, y)>0, such as
D( x, y)  k1 A( x. y)  k2 B( x, y)
(3)
with k1, k2 0 and k1+k2=1. That is, any interior
structural information, including texture, can be
incorporated in the deformation search as long as it
can be expressed by a single positive potential
function. From a pattern recognition or
discrimination view point, the proposed algorithm
provides an iterative partition or discrimination
scheme of having D(x, y) as a similarity measure
characterizing the interior with a similarity
threshold TV to explicitly isolate the interior region
from its surrounding rather than generating a
decision rule. For example, for a smooth interior
characterization, one may consider a function
D( x, y ) that consists of two components:
D( x, y )  A( x, y ) * B( x, y ) , with A( x, y ) being a
measurement of smoothness expressed as a function
of point gradient, and B ( x, y ) a measurement of
smoothness as a potential function of deviation from
an average brightness value I0 of the interior region
  (s ) . More specifically, these two components can
be defined as follows: A( x, y ) 

1
1  G*I ( x, y )
(4)
2
I ( x , y ) I 0

and B( x, y )  e
(5)
Therefore, D(x, y), as defined here, can be
interpreted as a homogeneity measure of
smoothness at an interior point (x, y). The large
value of the gradient and the large deviation of the
point brightness from I0 produce a much smaller
value of D(x, y). In other words, the threshold value
TV in the constraint is the lowest smoothness value
allowed in C . Thus, the contour optimization of E
in Eq. (1) would be subjected to this interior
homogeneity constraint and the constraint
D( x, y )  TV can be thought of as an interior
description of the contour C ( q, t ) and D( x, y ) can
be redefined to model the interior C .
In summary, proper imposition of constraints to
characterize the contour interior features may be
employed effectively on different specific
applications. In addition to the modeling of the
interior, modeling of the contour itself may further
assist the contour extraction process. We will see in
the next two subsections how two contour shape
models are added to the optimization process to
improve contour extraction results. They are the thin
plate spline matching method and the implicit
polynomial representation method.
2.2 Thin plate spline shape matching
The basic idea of the thin plate spline shape
matching is the calculation of the matching error
between a current contour and a model contour,
where the model contour is transformed to the
current contour space using thin plate spline method
to obtain the coordinate transformations, f x and
f y . To facilitate the computation of the coordinate
transformations, the matching distance is
approximated by the matching error between two
contour point sets sampled from the respective
continuous contours. More detailed discussion of
the above results can be found in [4].
2.2.1 Modified problem formulation
Our problem then is to find C(q,t) such that the
energy function E( ) is minimized, subject to the
region constraint D( ).
E (C (q, t ), M g (q ), f x , f y )  w
 g ( I (C (q, t )) )ds
0i , j
0i  j  n
C ( q ,t )
 (1  w) cs (C (q, t ), M (q ), f x , f y ),
(6)
g
0  w 1
D( x, y)  TV
xi y j
 a 00  a10 x  a 01 y  a 20 x 2  a11 xy    a 0 n y n
(11)
X A
if (x, y) c(t)
where
1
2
 dist (( x(q), y(q)), ( f x (u(q), v(q)), f y (u(q), v(q)))) dq
(7)
0
( x(q ), y (q )) and (u (q), v(q)) are contour points on
the continuous contour functions,  (q ) and M (q) ,
respectively.
dist 2 (( x(q), y (q)), ( f x (u (q), v(q)), f y (u (q), v(q)))
(8)
 ( x(q)  f x (u (q), v(q))) 2  ( y (q)  f y (u (q), v(q))) 2
2.2.2 Solution
The solution includes two alternating procedures:
curve evolution and shape matching. The formula
for curve evolution in the first procedure can be
defined as follows.


T
A  a00 a10 a01  a0n  and X  1 x y x 2 xy  y n .
A minimum least square approach using the
contour point set is applied to derive the coefficient
set A. The invariant feature set is then derived for
matching. The same operation on the model contour
to produce the invariant feature set is also executed.
The matching operation is the calculation of the
Mahalanobis distance. Detailed discussion can be
found in [5].
T
2.3.1 Modified problem formulation
Let the polynomial representation of C(q,t) be the
coefficient vector A.
Z f ( A)  ( x, y) : f ( x, y)  X T A  0
Our problem then is to find C(q,t) such that
E (C (q, t ))  w
 g ( I (C (q, t )) )ds 
C ( q ,t )

 
C (q, t )
 w kg( I )  (g  N ) N
t

 (1  w) D f ( x, y )  1[ D( x, y )  TV ] N

ij
T
where M g (q) is the shape model contour,
 cs ((q), M g (q), f x , f y ) 

a
f ( x, y ) 
(12)
(1  w)(   * ) T  g (   * ), 0  w  1
*
(9)

with
is minimized subject to the following constraints:
i) D( x, y)  TV
if (x, y) c(t)
1
 dist
( x(q, t ), y(q, t ), Z f ( A))dq  T f ,
D f ( x, y ) 
ii)
dist 2 (( x, y ), T ( M g ) if ( x, y ) is inside T ( M g ) ,

if ( x, y )  T ( M g )
0
 dist 2 (( x, y ), T ( M g ) if ( x, y ) is outside T ( M g )

where (   * )T  g* (   * ) represents the similarity
between the two shapes represented by the shape
features  from A and the model shape features  *
from the model coefficient vector A* derived from
fitting shape model M g (q) .  g* is the information
T (M g ) 
( f
x
0
(10)

(u (q ), v(q)), f y (u (q), v(q ))) : (u (q), v(q))  M g (q)
1  0 is the Lagrange multiplier, k is the contour

curvature and N is the normal direction.
In the shape matching procedure the goal is to
compute f x and f y by minimizing the matching
error between two equally spaced point sets
sampled from  (q ) and M (q) . Here, thin plate
spline method is used to find the solution.
2
matrix of  * . T f  0 is a constant.
2.3.2 Solution
The solution includes two alternating procedures:
curve evolution and shape matching. The resulting
curve evolution solution to this formulation is:

C (q, t ) 1 [ D( x, y )  TV ]
 N 

(13)
t
 wkg( I )  w(g  N )


 2 D f ( x, y ) N
2.3 Implicit polynomial shape representation
In here, a close contour is represented by a
polynomial of degree n in ( x, y ) as

with
dist 2 (( x, y ), Z f ( A)) , ( x, y ) inside Z f ( A)

D f ( x, y )  0
, ( x, y )  Z f ( A)

2
 dist (( x, y ), Z f ( A)), ( x, y ) outside Z f ( A)
and 2  0 is the Lagrange multiplier.
The shape matching procedure consists of
holding C(q,t) constant and minimizing Eq. (12) by
adjusting A.

A  2 X 3TL X 3 L  (1  w)Q( A* )
 (1  w)Q( A ) A
1
*
*
 2 X 3TL b
the average intensity and the standard deviation
inside the deforming contour C (q, t , Ti ) at

2.4 Pattern recognition consideration
As the recognition is now integrated in the contour
extraction process, the pattern recognition tasks
need to be considered. In this consideration, a
pattern class is defined as a set of different shape
models. Classification of a resultant contour shape
output, from either one of the methods as presented
in Sections 2.2 or 2.3, would be decided by its shape
distance measure between the obtained shape and a
given class model.
Once the constraints are defined, both the
interior and the contour model, we are ready to
present the contour optimization approaches using
the formulated constraints.
temperature Ti . 1C (Ti ) is the Lagrange multiplier.
(1) Curve evolution solution:
Variational based deformable contour searching, as
shown in Equation (14), with an MFA parameter
estimation scheme, is used.
C (q, t , T )

(14)
t


1* (T )D( x, y, T )  TV   kg( I )  g  N N
Level set numerical method is used.
(2) Interior characterization and constraint
( I ( x, y)  I 0 ) 2
D( x, y) 
 TV for all
 2


( x, y)  C (t ) , where   0 is a constant.
The MFA method treats the estimations of I 0
and  2 as functions of annealing temperature
Ti , i  1,n .
D( x, y, Ti ) 
3. Contour Optimization Approaches
This section presents the concepts for three
constrained optimization contour extraction
methods as well as their highlights. These
approaches, which provide global and local optimal
solutions using the level set numerical
implementations for extracting target contours in
images, include: the mean field annealing method,
variational method, and evolution strategy. For each
of the three approaches, a summary of the methods
features, such as the curve evolution formulation,
the interior characterization and the constraint,
analysis, and parameter estimation, is included.
3.1 Mean field annealing method
The Mean Field Annealing (MFA) method, as the
name indicates, uses the mean field annealing
approach to avoid local minima and to provide a
fast and efficient global approach to search for
constrained global optimal solutions to the problem
of object boundary extraction. Using this method,
with a given contour energy function, different
target boundaries can be modeled as constrained
global optimal solutions under different constraints
expressed as a set of parameters characterizing the
target contour interior structures. The method
derivation and a detailed discussion can be found in
[6]. The formulas have the following notation. Ti is
the annealing temperature. I 0C (Ti ) and  C2 (Ti ) are
Thus
the
constraint
becomes
( I ( x, y )  I 0 (Ti ))
 TV and I 0 and
 2 (Ti )
2
2
become I 0 (Ti ) and  2 (Ti ) .
(3) Analysis and optimality
* Lagrange approach
* Global solution
(4) MFA parameter estimations:
I 0 (Ti )  I 0C (Ti )
 2 (Ti )   C2 (Ti ) 
Ti

T
1* (Ti )  1C (Ti )  i

As an illustrative example, three target
boundaries in a synthetic image are modeled as
constrained global energy minimum contours with
different constraint parameters and are successfully
located using the derived algorithm. A conventional
variational based deformable contour method with
the same energy function and constraint fails to
achieve the same task. Experimental evaluations
and comparisons with other methods on ultrasound
pig heart, MRI knee, and CT kidney images where
gaps, blur contour segments having complex shape
and inhomogeneous interiors have been conducted
with most favorable results [6].
3.2 Variational Method
The variational method first takes a Lagrange
approach to the constrained optimization problem
and then uses a derivative based approach to derive
the curve evolution solution. As a result, the interior
constraint is reflected in this curve evolution
solution and act as a “balloon force” that can be
used to characterize any interior property and/or
structure including the “balloon force” used in the
geodesic snake [15] as a special case. The method
derivation and a detailed discussion can be found in
[2]. Here is a summary of the highlights for this
method.
(1) Curve evolution solution:
Variational based deformable contour searching
with Equation (15) is used.   0 is a constant.
C (q, t )
 ([ D( x, y )  TV ] 
(15)
t
 
kg( I )  (g  N )) N
Level set numerical method is used.
(2) Interior characterization and constraint
D( x, y )  TV for all ( x, y)  C (t ) . D( x, y ) can
be any function characterizing the interior;
(3) Analysis and optimality
* Lagrange approach
* Local solution
interior; D( x, y )  TV for all ( x, y)  C (t ) .
(3) Analysis and optimality
* Not a Lagrange approach
* Global solution is not guaranteed
N(b1, b2) indicates the Gaussian random variable
with mean ‘b1’ and standard deviation ‘b2’.
  Z1e  Z with
1
Z1 
I ( x, y )  M ( x, y )
1
and  1  2 .
M(x, y) is the local average intensity of size 3 by 3
with (x, y) being the center.
4 Applications with Sample Results
The comparison of these three different constrained
optimization approaches are made on the following
set of biomedical images: microscopic blood cell in
Fig. 2a, an MRI sagittal brain corpus callosum
image in Fig. 3a, two axial MRI brain images in
Fig. 4a and 5a, and a noisy CT kidney image in Fig.
6a.
The results of applying the three approaches are
shown in Figures 2-6: (b) the MFA method, (c) the
variational method, and (d) the evolution strategy,
respectively.
3.3 Evolution Strategy
The evolution strategy [19] is to mimic the process
of evolution in nature, the deriving process for
emergence of complex and well-adapted organic
structure. This evolution strategy is used to deform
C(s, t) until an optimum is reached. It is a recursive
process in which a population of individuals, the
parents, mutates and recombines to generate a large
population of offspring. These offspring are then
evaluated according to a fitness function and as a
result, a best subset of offspring is selected to
replace the existing parents. There are three main
factors to consider: (a) The representation of
individual contours (represented by states), (b)
variations of states, and (c) the selection scheme.
The method derivation and a detailed discussion can
be found in [1]. The highlights of this method are:
(1) Curve evolution solution:
Generation of a small population of candidate
contours and application of evolution strategy to
iteratively select a subset of contours with lowest
energies

C (q, t )
(16)
 ( D( x, y )(1  N (0,1))  TV ) N
t
Level set numerical method is used.
(2) Interior characterization and constraint
D( x, y ) can be any function characterizing the
(a)
(b)
(c)
(d)
Fig. 2 Blood cell microscopic image. (a) original
image. Results from (b) MFA method, (c)
variational, and (d) evolution method.
(a)
(b)
(c)
(d)
Fig. 5 Axial MRI brain image-2. (a) original,
(b) MFA, (c) variational, (d) evolution method.
(c)
(d)
Fig. 3 Brain corpus callosum image. (a) original,
(b) MFA, (c) variational, (d) evolution method.
(a)
(b)
(c)
(d)
Fig. 4 Axial MRI brain image-1. (a) original,
(b) MFA, (c) variational, (d) evolution method.
(a)
(b)
Fig. 4 Axial MRI brain image-2.
One of the implementation details is to select
the initial points. The three dark points in Fig. 3a
and Fig. 6a are the locations where the initial points
were chosen for the experiments.
(a)
(b)
(c)
(d)
Fig. 6 Noisy CT kidney image. (a) original,
(b) MFA, (c) variational, (d) evolution method.
Overall, from the sample results of Fig. 2
through Fig. 6, we can see that MFA method has the
best results comparing to those of the variational
method and evolution strategy. One major reason is
that the MFA is a global optimization method thus
is more robust to image noises and undesired local
energy minima.
As explained in Section 1, image understanding
can be greatly enhanced in applications where
object models can be incorporated into the object
segmentation and recognition process. Two contour
models were introduced in Section 2. The following
subsections will illustrate the results of using the
models in augmenting the image segmentation and
recognition.
4.1 Results using the thin plate spline model
The fruit image shown in Fig. 7a, containing two
apples, one banana, one cucumber, and one pear on
a 144 by 108 image, is obtained from [20] and used
here for illustration. We first use the apple model on
the algorithm with an initial seed region inside each
fruit object. The algorithm runs 5 times, one on each
fruit. The resulting five contours are shown in Fig.
7b. The matching measure is based on the shape
matching distance values, in terms of bending
energy Eb , as shown in column one of Table 1.
Apple II
Banana
Cucumber
Apple I
Pear
(a)
(b)
selecting the row minimum value as indicated by
(*). As one can see in Fig. 7, both Apple I and
Apple II contours are rather nicely segmented even
with Apple II touching the cucumber. Without the
apple model, one would have some difficulty
separating the two. The experiment is repeated for
the banana model, the cucumber model and the pear
model with the resulting contours shown in Figs. 7c,
7d and 7e, and Eb values in columns 2, 3 and 4, of
Table 1, respectively. The banana in Fig. 7c has the
best segmentation result noticing the dark banana
skin cover on the upper right side of the banana.
The cucumber in Fig. 7d has the best segmentation
among all other models in Figs. 7b, 7c and Fig. 7e.
Similar result can be reported on the pear in Fig. 7e.
All are successfully recognized.
The algorithm has also been successfully
applied on Fig. 8a, which is an image of size 300 by
400 consisting of two bananas partially occluded by
a cucumber.
(c)
Fig. 8. Fruit image-2, with overlapping objects.
(e)
(d)
Fig. 7
Fruit image. (a) original image. Results
using (b) the apple model, (c) the banana model, (d)
the cucumber model, and (e) the pear model.
Model
Bending Energy
Apple
Banana
Cucumber
Pear
Apple I
0.627*
1.361
1.276
1.773
Apple II
2.381
2.897
2.483
Banana
1.699*
4.88
0.498*
0.700
0.557
Cucumber
4.605
6.737
Pear
2.948
2.224
1.919*
2.349
1.954*
Object
3.477
Table 1. Resulting Performance Matrix
Our recognition decision is based on the
minimum Eb value on each object in using different
model assumptions as shown in Table 1, i.e.,
4.2 Results using the implicit polynomial model
Leaf image is used in the experiments with the
implicit polynomial model as presented in Section
2.3. There are two parts to our experiment.
Part 1 is to illustrate the segmentation capability
of the algorithm. Here, we use the leaf, marked with
an “X1”, as the model shown in Figure 9a. The final
segmentation result of leaf with a “Y12” mark in
Figure 9a is shown in Figure 9b. Figure 9c shows
the resulting segmentation contour using the same
velocity equation of Eq (13) without using the
model. Similarly, using “X2” of Figure 10a as model
provides a segmentation result of “Y22”on Figure
10b.
As for the illustration of the model selection
result, we compute the shape distance measure Dm
value of 4 leaves data, “Y11” and “Y12” for class 1 in
Figure 9a, and “Y21” and “Y22” for class 2 in Figure
10a. The resulting Dm using different models
deforming targets and classification decisions are
shown in Table 2. By selecting the lowest Dm
value, all classifications are correct in 4 classes.
5 Conclusion
(a)
(b)
(c)
Fig. 9 Leaf-1 image. (a) original.
(b) Segmented Leaf Y12 using Leaf X1 as a
model. (c) Without model.
(a)
(b)
Fig. 10 Leaf-1 image. (a) original.
(b) Segmented Leaf Y22 using Leaf X2 model.
Data(Deforming
Model)
Y11 (Model1)
Y11 (Model2)
Y12 (Model1)
Y12 (Model2)
Y21 (Model2)
Y21 (Model1)
Y22 (Model2)
Y22 (Model1)
DM
14.1
30.7
15.7
38.0
16.0
30.6
12.9
22.4
Class Decision
Class 1
Class 1
Class 2
Class 2
Table2 Model Selection Result
This paper presented a general contour constrained
optimization approach to object segmentation. By
integrating knowledge of image pattern structures,
both the contour interior and contour itself, in terms
of constraints and models into the formulation of the
solution for image processing, this approach sets up
a framework for a more holistic approach to object
understanding.
From a computational point of view, three
different approaches of mean field annealing
method, variational method, and evolutionary
strategy are presented to provide global and local
optimal solutions using level set numerical
implementations. Constraints that characterize the
contour interior features are employed on different
specific applications. Contour shape models using
either the thin plate spline matching method or the
implicit polynomial representation method are also
added into the optimization process to further
improve contour extraction results. A set of
illustrative examples for the applications of the
approaches on biomedical images and images of
natural objects are presented.
References:
[1] X. Wang, L. He, and W. Wee, “Deformable
Contour Method: A Constrained Optimization
Approach”, International Journal of Computer
Vision, (in press).
[2.] X. Wang, L. He, and W. Wee, "Constrained
Optimization: A Geodesic Snake Approach", vol.
II, Proc. IEEE International Conference of
Image Processing, 2002, pp.77-80.
[3] X. Wang, L. He, C. Y. Han, and W. Wee, "A
Constrained
Optimization
Approach
to
Deformable Contour Method", Proc. British
Machine Vision Conference, 2002, pp. 183-192.
[4] X. Wang, F. Gao, Z. Peng, L. He, and W. Wee,
“An Integrated Approach to the Segmentation
and Recognition of Objects using Thin Plate
Spline Method”, Proc. International Conference
of Vision Interfaces 2003, pp. 188-195.
[5] X. Wang, Z. Peng, F. Gao, and W. Wee, “A
Model Set Based Object Segmentation Method
Using Level Set Approach”, accepted by Digital
Image Computing Techniques and Applications
2003 (DICTA 2003).
[6] X. Wang, F. Gao, Z. Peng, L. He, and W. Wee,
"Mean Field Annealing Deformable contour
method A Global constrained optimization
Approach", submitted to IEEE Transactions on
Medical Imaging.
[7] Visible Human Project, http://www.nlm.nih.gov/
research/ visible/visible_human.html
[8] M. Kass, A. Witkin and D. Terzopoulos,
“Snakes: active contour models,” International
Journal of Computer Vision, Vol. 1, No.4, 1988,
pp. 321-331.
[9] L. Cohen, “On active contour models and
balloons,” CVGIP: Image Understanding, Vol.
52, No.2, March, 1991, pp.211-218.
[10] L. Cohen and I. Cohen, “Finite element
methods for active contour models and balloons
for 2-D and 3-D images,” IEEE Trans. on PAMI,
Vol. 15, No.11, Nov. 1993, pp. 1131-1147.
[11] C. Xu and J. Prince, “Snakes, shapes, and
gradient vector flow,” IEEE Trans. Image
Processing, Vol. 7, No. 3, Mar. 1998, pp. 359369.
[12] R. Malladi, J. Sethian and B. Vemuri, “Shape
modeling with front propagation”, IEEE Trans
on PAMI, Vol. 17, No.2, Feb. 1995, pp. 158-171.
[13] J. Sethian, “A fast marching level set method
for Monotonically advancing fronts,” Proc. Nat.
Acad. Sci., Vol. 93, No. 4, 1996.
[14] R. Malladi and J. Sethian, “A real time
algorithm for medical shape recovery,” ICCV,
1998. pp.304-310.
[15] V. Caselles, R. Kimmel and G. Sapiro,
“Geodesic active contours,” International
Journal of Computer Vision. Vol. 22, No. 1,
1997, pp. 61-79.
[16] G. Stovik, “A Bayesian Approach to Dynamic
Contours Through Stochastic Sampling and
Simulated Annealing,” IEEE Tran. Pattern
Analysis and Machine Intelligence, Vol.16,
1994, pp.976-986.
[17] A. Lundervold, G. Storvik, “Segmentation of
Brain Parenchyma and Cerebrospinal Fluid in
Multispectral Magnetic Resonance Images,”
IEEE Tran. Medical Imaging, Vol.14, 1995,
pp.339-349.
[18] R. Grzeszczuk, D. Levin, “’Brownian Strings’:
Segmenting
Images
with
Stochastically
Deformable Contours,” IEEE Tran. Pattern
Analysis and Machine Intelligence, Vol.19,
1997, pp.1100-1114.
[19] T. Back, U. Hammel, and H. Schwefel,
“Evolutionary computation: Comments on the
History and Current State,” IEEE Trans. On
Evolutionary Computation, Vol.1, No.1, 1997,
pp.3-17.
[20] S. Sclaroff, and L. Liu, “Deformable Shape
Detection Via Model Based Region Grouping,”
IEEE Trans. On PAMI, Vol. 23, No.5, May
2001, pp. 475-489.