Download Honors Geometry Unit #3 Lesson #1 Parallel Lines – are coplanar

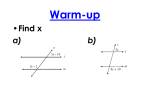
Honors Geometry
Unit #3 Lesson #1
Parallel Lines – are coplanar lines that do not intersect.
Euclidean Notation: “||” means parallel.
We mark parallel lines in a diagram by giving them arrows.
Example:
What happens when lines are parallel?
If lines are parallel, then
 corresponding angles are congruent. (Postulate)
 alternate interior angles are congruent. (Theorem)
 alternate exterior angles are congruent. (Theorem)
 same-side interior angles are supplementary. (Theorem)
 same-side exterior angles are supplementary. (Theorem)
How do we know that lines are parallel (when we don’t know their slopes?)?
If any of the above angle relationships are true, then the lines are parallel!
This means that lines are parallel if
 corresponding angles are congruent. (Postulate)
 alternate interior angles are congruent. (Theorem)
 alternate exterior angles are congruent. (Theorem)
 same-side interior angles are supplementary. (Theorem)
 same-side exterior angles are supplementary. (Theorem)
And …
Theorem: If two coplanar lines are perpendicular to a third line, they are parallel.
Theorem: In a plane, if a line is perpendicular to one of two parallel lines, it is perpendicular to the
other.
Theorem: If two lines are parallel to a third line, they are parallel to each other.
Honors Geometry
Unit #3 Assignment #1
Refer to the diagram below for each problem that says “see above”. In the diagram, l  m .
1
2
3 4
l
5
6
8
7
m
1. See above. If the m1 is given below, find the measure of each numbered angle.
a. m1 = 33
b. m1 = 168
c. m1 = x
2. See above. If m2 = 7x + 10 and m6 = 10x – 26, find m1 and m7.
3. See above. If m4 = 3x2 +10 and m6 = 15x +20, find m8.
4. See above. If m1 = 3x – y + 3, m4 = 8y – 3x, and m5 = 4x - 2y, find m3.
5. Find the value of each variable below.
a.
12x°
6x°
b.
(x2 + 4x)° y°
45°
80°
c.
68°
5x°
2z°
°
6. Identify all parallel lines in each diagram.
A
a. 1  2
1
B
C
E
2
D
P
Q
b.
S
R
c. 3 is supplementary to 4. (Hint: This is a trick question. There are only one pair of
parallel lines. Name them and draw another sketch of what the figure might look like.)
W
Z
X
3
4
Y
H
d.
K
G
L
J
e. 5 is supplementary to 6. 6 is supplementary to 7.
M
N
5
P
6
7
O

7. ST  XW and ST bisects VSW . Find mTSW , mVST , mX , and mW .
W
T
X
37°
S
V
8. In the diagram below, m1 = 15x – 3, m2 = 12x + 15, and m3 = 16x + 4. Is l  m ?
1
l
2
3
m
9. Find the values of x and y that make the bold lines parallel.
30°
5y°
2x°
(x – y)°
10. Graph the lines 2x + y = -12, x – 2y = -16, and y = 3x + 8.
a. These lines intersect to form a triangle. Find the coordinates of the vertices of the triangle.
b. Is the triangle a right triangle? Explain your answer.
c. Is the triangle an isosceles triangle? Explain your answer. (Hint, find the lengths of the
sides.)
U3A1 Key:
1. a. m4 = m5 = m8 = 33°
m2 = m3 = m6 = m7 = 147°
b. m4 = m5 = m8 = 168°
m2 = m3 = m6 = m7 = 12°
c. m4 = m5 = m8 = x°
m2 = m3 = m6 = m7 = (180 – x)°
2. m1 = 86° and m7 = 94°
3. 85°
4. 154°
5. a. x = 10; y = 60 b. x = -9 or 5; y = 55 c. x = 18; y = 43; z = 11
6. a. BE  CD b. PS  QR c. WX  YZ ;
d. GH  JK e. MN  PO and MP  NO
7. All angles measure 71.5°
8. No, m2 = 87° and m3 = 100°. The lines are not parallel b/c the angles are not supp.
9. x = 50; y = 20
10. a. (-8,4), (-4,-4), (0,8) b. Yes, slopes are -2 and 1/2. c. Yes, two sides have length 4 5 .