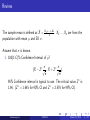Download Confidence Interval and Hypothesis Testing with unknown

Confidence Interval and Hypothesis Testing with
unknown σ
Kwonsang Lee
University of Pennsylvania
[email protected]
March 27, 2015
Kwonsang Lee
STAT111
March 27, 2015
1 / 17
Review
The sample mean is defined as X̄ =
population with mean µ and SD σ.
X1 +···+Xn
.
n
X1 , ..., Xn are from the
Assume that σ is known,
1. 100(1-C)% Confidence Interval of µ?
σ
σ
(X̄ − Z ∗ √ , X̄ + Z ∗ √ ).
n
n
95% Confidence interval is typical to use. The critical value Z ∗ is
1.96. (Z ∗ = 1.645 for 90% CI and Z ∗ = 2.576 for 99% CI).
Kwonsang Lee
STAT111
March 27, 2015
2 / 17
Review
2. Hypothesis test?
a. State the null and alternative hypotheses. (Here, two-sided example)
H0 : µ = µ0
and Ha : µ 6= µ0 .
b. Calculate a test statistic Z0
Z0 =
X̄ − µ0
√ .
σ/ n
c. Calculate the P-value
P-value = P(Z ≥ |Z0 |) + P(Z ≤ −|Z0 |)
= 2 · P(Z ≥ |Z0 |)
(or 2 · P(Z ≤ −|Z0 |))
d. Compare the P-value to the significance level α
Note: Z ∼ Normal(0, 1).
Kwonsang Lee
STAT111
March 27, 2015
3 / 17
Relationship between CI and hypothesis test
1) Constructing a 95% Confidence interval and
2) conducting hypothesis test with the two-sided alternative hypothesis
and the significance level α = 0.05 are very similar.
In other words, the null hypothesis H0 : µ = µ0 will be rejected at the level
α = 0.05 if the 95% CI does not contain µ0 .
Note: Two sided level α hypothesis test ⇒ 100(1 − α)% CI
Kwonsang Lee
STAT111
March 27, 2015
4 / 17
Question 2 (last week): Risk of high-tech stocks
There is a random sample of 15 high-technology stocks.
x̄ = 1.23,
σ = 0.37
We want to test the null hypothesis H0 : µ = 1. In this case, µ0 = 1.
Under the null H0 : µ = 1, the test statistic Z0 is given by
Z0 =
1.23 − 1
√ = 2.41.
0.37/ 15
The p-value for the two-sided alternative is
P-value = P(Z > 2.41) + P(Z < −2.41)
= 2 × P(Z > 2.41)
= 2 × 0.0080 = 0.0160.
Therefore, we reject the null hypothesis under the level α = 0.05.
Kwonsang Lee
STAT111
March 27, 2015
5 / 17
Question 2
We can do this by calculating the 95% Confidence interval of µ.
The 95% CI is
σ
σ
0.37
0.37
(x̄ − 1.96 √ , x̄ + 1.96 √ ) = (1.23 − 1.96 √ , 1.23 + 1.96 √ )
n
n
15
15
= (1.04, 1.42)
(1.04, 1.42) does not contain µ0 = 1, so we reject the null.
Note: If the null hypothesis was H0 : µ = 1.1, then we don’t reject this
new null hypothesis.
Kwonsang Lee
STAT111
March 27, 2015
6 / 17
What if σ is unknown?
We assumed that we know the standard deviation σ. If we don’t know it,
then we need a different approach.
From the sample of size n, we can find the sample mean
x̄ =
x1 + · · · + xn
n
and also find the sample standard deviation s
sP
n
2
i=1 (xi − x̄)
s=
n−1
We will use s instead of σ to make inferences.
Kwonsang Lee
STAT111
March 27, 2015
7 / 17
Distribution under unknown σ
From Central Limit Theorem, when σ is known, we can use
Z=
X̄ − µ
√ ∼ Normal(0, 1)
σ/ n
When σ is unknown, we use
T =
X̄ − µ
√ ∼ t(n − 1)
s/ n
where t(n − 1) is the t-distribution with n − 1 degrees of freedom.
Kwonsang Lee
STAT111
March 27, 2015
8 / 17
t-distribution
Kwonsang Lee
STAT111
March 27, 2015
9 / 17
Properties of t-distribution
Again, t(n) is the t-distribution with n degrees of freedom.
1. As n approaches to ∞, t(n) → N(0, 1).
2. t-distribution has heavy tails.
3. Approximately, when n > 30, it’s okay to see Normal table instead of
t-table.
t-table ⇒ http:
//bcs.whfreeman.com/ips6e/content/cat_050/ips6e_table-d.pdf
Kwonsang Lee
STAT111
March 27, 2015
10 / 17
Confidence interval when σ is unknown
Now, we construct a 100(1-C)% Confidence Interval for unknown
population mean µ.
s
s
∗
∗
√ , X̄ + tn−1
√ )
(X̄ − tn−1
n
n
∗
where tn−1
is the critical value.
We need to see the row of df= n − 1 and the column of p =
C
2
Important! For example, when n = 10 and 95% CI, degrees of freedom
(df) is 9 and p = 0.025. Therefore, the critical value of the 95% CI is
t9∗ = 2.262.
Kwonsang Lee
STAT111
March 27, 2015
11 / 17
Quick Question
We can consider
a. 95% CI when σ is known (normal distribution based approach) and
b. 95% CI when σ is unknown (t-distribution based approach).
Then, which one is wider between a. and b.?
A: Intuitively, b. is wider because there is more uncertainty (especially,
uncertainty of σ). In fact, the critical values are Z ∗ = 1.96 and t9∗ = 2.262
respectively.
Kwonsang Lee
STAT111
March 27, 2015
12 / 17
Example: CI with unknown σ
Let’s go back to Question 2 discussed last week. We have a random
sample of size 15 high-tech stocks. Now, we assume that the sample mean
x̄ = 1.23 and the sample standard deviation s is 0.37. The population
standard deviation σ is unknown.
∗ is 2.145 and the 95% CI for the population
Then, the critical value t14
mean µ is
s
0.37
0.37
s
∗
∗
√ , X̄ + tn−1
√ ) = (1.23 − 2.145 · √ , 1.23 + 2.145 · √ )
(X̄ − tn−1
n
n
15
15
= (1.03, 1.43).
Note: When we have σ = 0.37, the 95% CI was (1.04, 1.42).
Kwonsang Lee
STAT111
March 27, 2015
13 / 17
Hypothesis test with unknown σ
If the population SD σ is unknown, we need to compute p-value using
t-distribution, but the steps are the same.
a. State the null hypothesis H0 and the alternative hypothesis Ha .
b. Compute the test statistic T0 .
T0 =
X̄ − µ0
√
s/ n
c. Calculate the p-value


P(T > |T0 |) + P(T < −|T0 |)
P-value = P(T > T0 )


P(T < T0 )
if Ha : µ 6= µ0
if Ha : µ > µ0
if Ha : µ < µ0
d. Compare the p-value with the significance level α.
Kwonsang Lee
STAT111
March 27, 2015
14 / 17
Question 1
Summary: n = 25, x̄ = 44.1 and s = 6.2. We want to test if the mean of
self-worth for male heroin addicts = 48.6.
a. The null hypothesis is H0 : µ = 48.6 and the alternative hypothesis is
Ha : µ 6= 48.6.
b. The test statistic T0 is given by
T0 =
Kwonsang Lee
44.1 − 48.6
x̄ − µ0
√
√ =
= −3.63
s/ n
6.2/ 25
STAT111
March 27, 2015
15 / 17
Question 1
c. P-value is calculated by
p-value = P(T > 3.63) + P(T < −3.63)
= 2 · P(T < −3.63) = 2 · 0.0007
= 0.0014
Comment: Again, we can’t find the probability P(T > 3.63) from
the t-table. We need a statistic software that can compute it.
Instead, we can use another approach like part e. without computing
the p-value.
d. It is significant because p-value 0.0014 is less than α = 0.01, which
means we reject the null hypothesis.
Kwonsang Lee
STAT111
March 27, 2015
16 / 17
Question 1
e. α = 0.01 corresponds to a 99% CI. When n = 25, the critical value
∗ is 2.797 from df= 24 and Upper-tail probability p = 0.005.
t24
The 99% CI is
s
6.2
6.2
s
∗
∗
√ , X̄ + tn−1
√ ) = (44.1 − 2.797 · √ , 44.1 + 2.797 · √ )
(X̄ − tn−1
n
n
25
25
= (40.6, 47.6).
µ0 = 48.6 is not contained in the 99% CI, (40.6, 47.6). Therefore, we
reject the null.
Kwonsang Lee
STAT111
March 27, 2015
17 / 17