Download Trees

CSE 326: Data Structures
Trees
Lecture 6: Friday, Jan 17, 2003
1
Trees
Material: Weiss Chapter 4
• N-ary trees
• Binary Search Trees
• AVL Trees
• Splay Trees
2
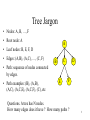
Tree Jargon
• Nodes: A, B, …, F
• Root node: A
A
• Leaf nodes: B, E, F, D
• Edges: (A,B), (A,C), …, (C, F)
C
B
D
• Path: sequence of nodes connected
by edges.
• Path examples: (B), (A,B),
(A,C), (A,C,E), (A,C,F), (C), etc
E
F
Questions. A tree has N nodes.
How many edges does it have ? How many paths ?
3
Tree Jargon
• Length of a path =
number of edges
• Depth of a node x =
length of path from
root to x
• Height of node x =
length of longest
path from x to a leaf
• Depth and height of
tree = height of root
depth=0, height = 2 A
B
depth = 2, height=0 E
C
D
F
• The label of a node:
A, B, C, …
4
Definition and Tree Trivia
Graph-theoretic definition of a Tree:
A tree is a graph for which there exists a node, called
root, such that:
-- for any node x, there exists exactly one path
from the root to x
Recursive Definition of a Tree:
A tree is either:
a. empty, or
b. it has a node called the root, followed by zero or
more trees called subtrees
5
Implementation of Trees
• Obvious Pointer-Based Implementation: Node with
value and pointers to children
– Problem?
A
C
B
E
D
F
6
1st Child/Next Sibling
Representation
• Each node has 2 pointers: one to its first child and
one to next sibling
A
A
C
B
E
D
F
C
B
E
D
F
7
Nested List Representation
• Each node has a pointer to a list containing its
children
A
A
C
B
E
D
F
C
B
E
D
F
8
Application: Arithmetic
Expression Trees
Example Arithmetic Expression:
+
A + (B * (C / D) )
A
*
Tree for the above expression:
• Used in most compilers
• No parenthesis need – use tree structure
• Can speed up calculations e.g. replace
/ node with C/D if C and D are known
• Calculate by traversing tree (how?)
B
/
C
D
9
Traversing Trees
+
• Preorder: Root, then Children
– +A*B/CD
A
*
• Postorder: Children, then Root
– ABCD/*+
B
• Inorder: Left child, Root, Right child
/
– A+B*C/D
D
C
10
Example Code for Recursive
Preorder
void print_preorder ( TreeNode T)
{ if ( T == NULL ) return;
print_element(T.Element());
print_preorder(T.FirstChild());
print_preorder(T.NextSibling());
}
What is the running time for a tree with N nodes?
11
Binary Trees
• Properties
– max # of leaves = 2depth(tree)
– max # of nodes = 2depth(tree)+1 – 1
A
• We care a lot about the depth:
– max depth = n-1
– min depth = log(n) (why ?)
– average depth for n nodes = n
(over all possible binary trees)
B
D
C
E
F
• Representation:
TreeNode:
G
Element
Left
Right
I
H
J
12
Binary Trees
Notice:
• we distinguish between left child
and right child
A
B
A
C

B
C
F
G
F
H
G
H
13
Binary Search Tree
• Search tree property
– all keys in left subtree
smaller than root’s key
– all keys in right subtree
larger than root’s key
– result:
• easy to find any given
key
• inserts/deletes by
changing links
8
5
2
11
6
4
10
7
9
12
14
13
14
Searching in a Binary Search
Tree
Boolean find(int x, TreeNode T)
{ if ( T == NULL )
return false;
if (x == T.Element)
return true;
if (x < T.Element)
return find(x, T.Left);
return find(x, T.Right);
}
10
5
2
15
9
7
20
17
30
What is the running time ?
15
Insert a Key
TreeNode insert(int x, TreeNode T)
{ if ( T == NULL )
return new TreeNode(x,null,null);
if (x == T.Element)
return T;
if (x < T.Element)
T.Left = insert(x, T.Left);
else T.Right = insert(x, T.Right);
return T;
}
10
5
2
3
15
9
7
20
17
What is the running time ?
30
16
Delete a Key
How do you delete:
10
5
17 ?
15
9?
2
9
20
20 ?????
7
17
30
17
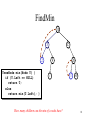
FindMin
10
5
15
2
TreeNode min(Node T) {
if (T.Left == NULL)
return T;
else
return min(T.Left); }
9
7
How many children can the min of a node have?
20
17 30
18
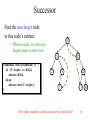
Successor
Find the next larger node
in this node’s subtree.
10
– When it exists, it is the next
largest node in entire tree
5
TreeNode succ(TreeNode T) {
if (T.right == NULL)
return NULL;
else
return min(T.right);
}
15
2
9
7
How many children can the successor of a node have?
20
17 30
19
Deletion - Leaf Case
10
Delete(17)
5
15
2
9
7
20
17 30
20
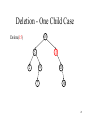
Deletion - One Child Case
10
Delete(15)
5
15
2
9
7
20
30
21
Deletion - Two Children Case
10
Delete(5)
5
20
2
9
30
7
replace node with value guaranteed to be between the left and
right subtrees: the successor
22
Deletion - Two Children Case
10
Delete(5)
5
20
2
9
30
7
always easy to delete the successor – always has either 0 or 1
children!
23
Deletion - Two Child Case
10
Delete(5)
7
20
2
9
30
7
Finally copy data value from deleted successor into original
node
What is the cost of a delete operation ?
Can we use the predecessor instead of successor ? 24
Cost of the Operations
• find, insert, delete :
time = O(height(T))
• Need to compute height(T)
• For a tree T with n nodes:
– height(T)  n
– height(T)  log(n)
(why ?)
25
Height of the Binary Search Tree
• Height depends critically on the order in which we
insert the data:
– E.g. 1,2,3,4,5,6,7 or 7,6,5,4,3,2,1, or 4,2,6,1,3,5,7
7
1
4
2
6
2
5
3
6
4
4
3
2
1
3
5
7
5
6
7
1
Which insertion order corresponds to what tree ?
Which tree do we prefer and why ?
26
The Average Depth of a BST
• Insert the elements 1 <2 < ... < n in some order,
starting with the empty tree
• For each permutation, :
– T = the BST after inserting (1), (2) , ... , (n)
• The Average Depth:
H(n)  ( height(T π ))/n!
π
• Let’s compute it !
27
The Average Depth of a BST
• H(n) seems hard, let’s compute something
else instead
• The internal path length of a tree T is:
depth(T) = sum of all depths of all nodes in T
• Clearly depth(T)/n  height (T)
(why ?)
• The average internal path length is:
D(n)  ( depth(T π ))/n!
π
28
The Average Depth of a BST
• Compute D(n) now:
n
D(n)  (
 depth(T
i 1 π(1)i
n
 (( 
π
))/n! 
 depth(Left (T ))  depth(Righ t(T )))/n! 
i 1 π(1)i
π
π
1 n
   depth(Left (Tπ ))/(n - 1)!depth(Righ t(Tπ ))/(n - 1)! 
n i 1 π(1)i
1 n
2 n -1
  (D(i  1)  D(n  i)  (i  1)  (n  i))   D(i)  n  1
n i 1
n i 1
29
The Average Depth of a BST
• Compute D(n) now:
2 n -1
D(n)   D(i)  n  1
n i 1
n D(n)
= 2i=1,n-1D(i) + n(n – 1)
(n-1) D(n-1) = 2i=1,n-2D(i) + (n – 1)(n – 2)
n D(n) – (n – 1) D(n-1) = 2D(n-1) +2(n – 1)
n D(n)
= (n+1)D(n-1) + 2(n – 1)
D(n)/n+1
= D(n-1)/n + 2(n-1)/n(n+1)
< D(n-1)/n + 2/n
D(n)/n+1
D(n)
H(n)
< 2( 1/n + 1/(n-1) + ... + 1/3 + 1/2 + 1)  2log(n)
= (n log n)
30
= (log n)
The Average Depth of a BST
• What have we achieved ?
• The average depth of a BST is:
H(n) = (log n)
31
n versus log n
Why is average depth of BST's made from
random inputs different from the average
depth of all possible BST's?
log n
n
Because there are more ways to build shallow
trees than deep trees!
32
Random Input vs. Random Trees
For three items, the
shallowest tree is
twice as likely as
any other – effect
grows as n
increases. For n=4,
probability of
getting a shallow
tree > 50%
Inputs
1,2,3
3,2,1
1,3,2
3,1,2
2,1,3
2,3,1
Trees
33
Average cost
• The average, amortized cost of n insert/find
operations is O(log(n))
• But the average, amortized cost of n
insert/find/delete operations can be as bad as
sqrt(n)
– Deletions make life harder (recall stretchy arrays)
– Read the book for details
• Need guaranteed cost O(log n) – next time
34