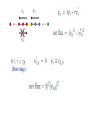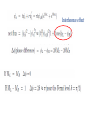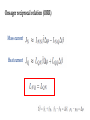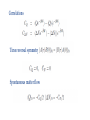* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint
Canonical quantization wikipedia , lookup
Technicolor (physics) wikipedia , lookup
Noether's theorem wikipedia , lookup
Atomic theory wikipedia , lookup
Tight binding wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Yang–Mills theory wikipedia , lookup
Particle in a box wikipedia , lookup
Renormalization wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Scalar field theory wikipedia , lookup
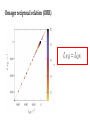
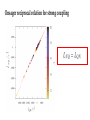
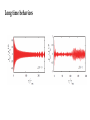
Nonequilibrium matter exchange between finite quantum systems Juyeon Yi (Pusan National University) Euijin Jeon and Yong Woon Kim (KAIST) Matter moves… Oliver Lodge For quantum mechanical systems, steady state can exist even when they are isolated Fermi’s golden rule total transition probability Transition rate is constant in time Question If two systems are large enough, can we expect steady state (SS) in which constant matter current flows? No ! If SS exists, we reach a unphysical situation where current flows from an empty bucket Grasp a picture through an example… 1D tight-binding fermions Initial equilibrium end-point coupling System parameters temperatures, chemical potentials, sizes, band widths, coupling strength (energy band width) Quasi-continuum (level spacing) (inter chain coupling) Nearly half filling (intra chain coupling) Weak coupling mass current vs normalized time (current from high to low chemical potential system) what are the normalization constants? Landauer-Buettiker formula for currents between infinite systems Roundtrip time of a particle moving with the Fermi velocity size dependence backflow (current from high to low chemical potential system) scattering picture (from the right to the left) (First stage ) Second stage (wave number ) × (path length) Interference effect Roundtrip along the left system is concurrent with the round trip along the right system at 𝝉 = 𝟐𝝉𝑹 Onsager reciprocal relation (ORR) Mass current Heat current Onsager reciprocal relation (ORR) Landauer formula and Onsager relation Transient fluctuation theorem Jarzynski and Wojcik (2004 Phys. Rev. Lett. 92, 230602) number exchange : energy exchange : Mass current Heat current total energy change : If 1 Onsager symmetry exists ! Onsager reciprocal relation for strong coupling More generally for correlations Correlations Time reversal symmetry Spontaneous matter flow and are also Onsager symmetric. Onsager relation also holds if heat and number change are strongly correlated with large values of W Bennett weighting factor Long time behaviors Disorder effects