Download Directions - James Rahn

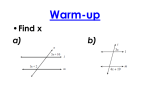
Slide 1: This slide contains an infinitely cloned triangle that can be used to do the following as students
do it on a sheet of patty paper.
-
-
Have students draw an obtuse triangle with their rulers on a sheet of paper. Label the angles A,
B, and C. (The triangle should be small enough so three of the triangles will fit on a sheet of
patty paper when placed next to each other.) Using a sheet of patty paper have students draw a
duplicate of the triangle in the center of a sheet of patty paper.
Have students make a duplicate of the same triangle next to the first triangle but turned upside
down. Model this on the smartboard. Mark the angles appropriately.
Have students add a third triangle on the other side of the first triangle. Mark the angles
appropriately. Model this on the smartboard.
Add the two parallel lines to the diagram, but leave off the green transversal. Analyzing the diagram.
Ask students to notice the three angles of the triangle are A, B, and C. Do the students see angles A, B,
and C together in the picture any place else other than in a triangle? They should notice that the three
angles form a line. Help students tie the thoughts together that since the 3 angles make a straight line
they must total to 180 degrees.
There are many lines that could be transversals. Identify one as a transversal. Identify the two angle C’s
that are alternate interior angles. Identify some other angles that would be congruent in the diagram.
Discuss which angles are congruent and which angles are supplementary.
Slide 2: This slide shows two parallel lines and the transversals. It is the same as slide 1 should have
finished. Develop which angles are congruent and which add up to 180 degrees from the diagram by
sliding a triangle over to the picture.
Slide 3: Try labeling this picture from what students remember from slide 2. Slide over the triangle if
help is needed.
Slide 4: Find as many angles as possible in this picture. Name angles as students find them. Look for
congruent pairs and supplementary pairs.
Slide 5: What do we know about each of these angles? How can we state that algebraically? What is
the side of each angle?
Slide 6: What do we know about each of these angles? How can we state that algebraically? What is
the side of each angle?
Slide 7: What do we know about each of these angles? How can we state that algebraically? What is
the side of each angle?
Slide 8: What do we know about each of these angles? How can we state that algebraically? What is
the side of each angle?
Slide 9: What do we know about each of these angles? How can we state that algebraically? What is
the side of each angle?
Slide 10: Find the measure of as many angles as you can in the drawing.