Download Derive - Shelton State

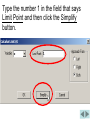
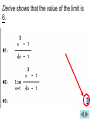
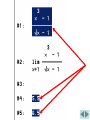
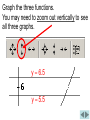
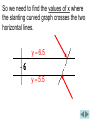
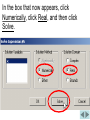
PROBLEM 40
FROM
SECTION 2.2
Problem 40: (a) Use numerical and
graphical evidence to guess (we will use
the limit capability of Derive instead) the
3
x 1
value of the limit lim
.
x 1 x  1
(b) How close to 1 does x have to be to
ensure that the function in part (a) is
within a distance 0.5 of its limit?
OUTLINE OF THE SOLUTION PROCESS
x3  1
is 6.
1. Use Derive to find that lim
x 1 x  1
3
x 1
2. Solve for x in the equation
 5.5.
x 1
3. Call this solution x1.
3
x 1
4. Solve for x in the equation
 6.5.
x 1
5. Call this solution x 2.
6. Find the smaller of x1  1 and x2  1
and round the result down.
3
x 1
. To do this,
Use Derive to find lim
x 1 x  1
type and enter  x ^ 3  1
the Derive screen.


x  1 on
Click the lim (limit) button on the upper
toolbar.
The following box will then appear (see
next slide).
Type the number 1 in the field that says
Limit Point and then click the Simplify
button.
Derive shows that the value of the limit is
6.
Now we will work part (b) of number 40:
How close to 1 does x have to be to ensure
that the function in part (a) (let’s call it f) is
within a distance 0.5 of its limit?
3
x 1
So we want f  x  
to be within 0.5
x 1
of 6.
For f(x), that is, y, to be within 0.5 of 6 means
that y is between 6  0.5 and 6  0.5.
In other words, y is between 5.5 and 6.5.
We need to graph the following functions
on the same screen:
x3  1
y
,
x 1
y  5.5, and
y  6.5
On the Derive screen type and enter 5.5,
and then type and enter 6.5.
Hold down the Ctrl key on the computer
keyboard and click on the fraction, on 5.5,
and on 6.5, so that all three are
highlighted. (See next slide.)
Graph the three functions.
You may need to zoom out vertically to see
all three graphs.
y  6.5
y  5.5
We need to find where the graph of
3
x 1
is between the horizontal
f x 
x 1
graphs of y  5.5 and y  6.5.
y  6.5
y  5.5
So we need to find the values of x where
the slanting curved graph crosses the two
horizontal lines.
y  6.5
y  5.5
Go back to the algebra screen and type
3
x 1
 5.5.
and enter the equation
x 1
Use Derive to solve this equation.
Click the Solve button.
In the box that now appears, click
Numerically, click Real, and then click
Solve.
Derive displays the solution.
Call this solution x1.
Now go back to the Algebra screen on
Derive and repeat the previous steps
to solve for x in the equation
3
x 1
 6.5.
x 1
Derive displays the solution.
Call this solution x 2 .
To finish the problem, find the smaller of
x1  1 and x 2  1.
Then round this result down.
x1  1  0.9313853085  1
 0.06861469149
So x1  1  0.06861469149
Similarly, x 2  1  0.064900383
Round the smaller result down to, say,
three decimal places.
Then the final answer is 0.064.