Download Poly Gizmo directions

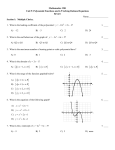
Algebra 2/Trig
Polynomials
Name ______________________
Date __________Block _______
In this Gizmo, Fourth-Degree Polynomials Activity A, you will explore the relationship between the
leading coefficient and the end behavior of a polynomial function. Follow the instructions below and
complete the following.
1. Adjust sliders a and b to zero. Move c to 1, d to -1, and f to -6.
2. Write the resulting equation here.________________________
3. What type of equation do you see?____________________ What is the degree of this
polynomial? ______________ What is the leading coefficient? _____________________
4. Factor and solve the equation in number 2 above.
5. Verify that the x-intercepts match your solution above (hint: you can click on show
intercepts) .
6. What is the y-intercept? __________ Where do you see this number in the equation in
number 2 above? ______________
7. Which direction are the ends of the graph pointing?__________________
8. Adjust the c slider to -1 and the f slider to 6. What do you observe about the graph?
_______________________________________________________________________
9. Write the resulting equation here.________________________
10. What type of equation do you see?____________________ What is the degree of this
polynomial? ______________ What is the leading coefficient? _____________________
11. Factor and solve the equation in number 9 above.
12. Verify that the x-intercepts match your solution above.
13. Which direction are the ends of the graph pointing now?__________________
14. How do you think the degree of the polynomial and the leading coefficient impact the
ends of the graph?
15. Leaving the a slider at 0, adjust the b to 1, the c to -1, and the d to -6. F remains zero.
16. Write the resulting equation here.________________________
17. What type of equation do you see?____________________ What is the degree of this
polynomial? ______________ What is the leading coefficient? _____________________
18. Factor and solve the equation in number 16 above.
19. Verify that the x-intercepts match your solution above (hint: you can click on show
intercepts) .
20. What is the y-intercept? __________ Where do you see this number in the equation in
number 16 above? ______________
21. Which direction are the ends of the graph pointing?________________________________
_____________________________________________________________________________
22. Leaving a at 0, adjust slider b to -1, c to -5, and d to -6. F remains zero.
23. Write the resulting equation here.________________________
24. What type of equation do you see?____________________ What is the degree of this
polynomial? ______________ What is the leading coefficient? _____________________
25. Factor and solve the equation in number 23 above.
26. Verify that the x-intercepts match your solution above
(hint: you can click on show intercepts).
27. Which direction are the ends of the graph pointing now?__________________________
___________________________________________________________________________
28. How do you think the degree of the polynomial and the leading coefficient impact the
ends of these graphs?
29. Adjust slider a to 1, b to 0, c to -5, d to 0, and f to 4.
30. Write the resulting equation here.________________________
31. What type of equation do you see?____________________ What is the degree of this
polynomial? ______________ What is the leading coefficient? _____________________
32. Factor and solve the equation in number 30 above.
33. Verify that the x-intercepts match your solution above (hint: you can click on show
intercepts) .
34. What is the y-intercept? __________ Where do you see this number in the equation in
number 30 above? ______________
35. Which direction are the ends of the graph pointing?________________________________
This end behavior should be exactly the same as the quadratic equation with the positive
leading coefficient.
37. Predict which directions the ends would be going if the leading coefficient was negative for
this equation. _________________________________________________________________
38. If you were given the equation: y  x5  3x 4  2x 2  6x  1 , which direction do you
think its ends would be pointing? (hint: think about the cubic function) _________________
___________________________________________________________________________
39. How would the end behavior change if the leading coefficient of the equation above (in
number 38) is negative?
_______________________________________________________________________
40. Describe the different end behaviors you have observed in this lesson?_________________
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
Based on your observations, complete the chart below.
Leading
Coefficient
Degree
as
positive
even
negative
even
positive
odd
negative
odd
x  
as
x  
x   means as x approaches negative
x   means as x approaches positive infinity
Assessment Questions
1.
What is the degree, leading coefficient, and end behavior of the polynomial function
y  4 x 2  3x  7 ?
2. What is the lowest possible degree of the equation in the graph shown below?
3. What is the maximum number of x-intercepts that can be found on a graph with
equation y = ax5 + cx2 + f, where a, c, and f are any real numbers?
4. What is the end behavior of y = −2x13 + 25x8 − 3 as x approaches infinity?