* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Create a table of values for the relation.
Survey
Document related concepts
Mathematics of radio engineering wikipedia , lookup
System of polynomial equations wikipedia , lookup
Line (geometry) wikipedia , lookup
Elementary algebra wikipedia , lookup
Recurrence relation wikipedia , lookup
Partial differential equation wikipedia , lookup
Transcript
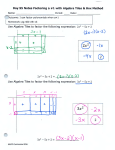
Math 8 – Linear Equations and Graphing (Chapter 6 in Math Makes Sense) Teacher Name:____________________________ 6.0 Activating Prior Knowledge Skill one: Graphing ordered pairs: An ordered pair such as (4, 2) tells you the position of a point on a grid. The first number is the horizontal distance from the origin (0,0). The second number is the vertical distance from the origin. The numbers of an ordered pair are also called the coordinates. Notice how the grid is divided into four sections called quadrants, which are made by the x axis (the horizontal) and the y axis (the vertical). All points in the first quadrant have positive values for both x and y (x,y). All points in the second quadrant have negative values for x and positive values for y ( -x,y) All points in the third quadrant have negative values for both x and y (-x, -y) All points in the fourth quadrant have positive values for x and negative values for y (x,-y) Write the coordinates for points B, C, and D and state the quadrant that they are in. B ( , ) quadrant _____ C ( , ) quadrant ______ D ( , ) quadrant _______ Skill Two: Solving Equations Using Algebra Tiles Recall that integers can be represented using tiles. -1 +1 We can represent variables using tiles as well. -x +x The expression that is represented by is __________. What equation is being modeled: ________________________ = 6.1 Solving equations using models We can use the model concept to solve equations using algebra tiles. Solve: x – 3 = 8 (mentally picture the scale) To cancel out these represents the equal sign we must add the opposite REMEMBER: WHAT YOU DO TO ONE SIDE YOU MUST DO TO THE OTHER! We can also use algebra tiles to solve an equation: 3j – 5 = 19 Example1: Use algebra tiles to solve: 2x + 4 = -2 Example 2: Use algebra tiles to solve -2x – 6 = 8 Example 3: Three more than six times a number is 21. Let x represent the number. a) Write an equation you can use to solve for x. ____________________ b) Represent the equation with tiles and use the tiles to solve the equation. 6.2 Using Equations Using Algebra We can solve an equation using algebra. To help us visualize the equation, we think about a model, such as a balance scales or algebra tiles. To solve an equation, we need to isolate the variable on one side of the equation. To do this, we get rid of the numbers on that side of the equation by performing the opposite operation to both sides of the equation. When we solve an equation using algebra, we must also preserve the equality or balance. Whatever we do to one side of the equation, we must do to the other side, too. Example one: 2x – 3 = 7 Example two: -3x + 4 = -2 Example three: 𝑥 3 − 2=1 Example four: Seven more than three times a number is eight. Find the number. Homework: 6.3 Solving Equations Involving Fractions 3 Which number could you multiply by to get the product of 3? 7 5 Which number could you multiply by to get the product of 5? 6 Solve each equation: a) d) 𝑛 4 𝑡 5 =6 + 3 = 10 𝑎 𝑐 b) = 8 c) = 9 7 3 𝑥 e) 13 + = 25 2 f) 𝑥 5 -1=9 Homework: 𝑥 g) - 9 + = 2 2 6. 4 The Distributive Property Example One: Example 2: Example 3: Use the distributive property to write each expression as a sum of terms. Sketch a diagram in each case. a) 7( c + 2 ) b) 42 ( a + b) Example 4: Expand a) 6( x-3) b) 5( 8 – c) c) - 4 (- 6 – x) Example 5: Use algebra tiles to show that 5(x + 2) and 5x + 10 are equivalent. Homework: 6.5 Solving Equations Involving the Distributive Property The distributive property is needed to solve some algebraic equations. Examples: a) 3(x + 5) = 36 d) - 2( a + 4 ) = 18 b) 4( p – 6 ) = 36 e) – 3 ( r – 5 ) = -27 c) 5 ( y + 1 ) = -10 f) -6 ( c – 9 ) = - 42 g) Marc has some hockey cards. His friend gives him 3 more cards. Marc says that if he now doubles the number of cards he has, he will have 20 cards. How many cards did Marc start with? a) Choose a variable to represent the number of cards Marc started with? b) Write an equation to model this problem. c) Solve the equation using the distributive property. h) The perimeter of a rectangle is 26cm. The rectangle has length 8 cm. What is the width of the rectangle? a) Choose a variable to represent the width of the rectangle? a) Write an equation to model this problem. b) Solve the equation using the distributive property. Homework: 6.6 Creating a Table of Values We can represent a relation in different ways. For example, consider this relation; x is related to 20 - 3x. Example one: a) Use the equation to create a table of values. n c 0 1 2 3 b) Use the equation to find the cost of a pizza with 5 toppings. c) Use the equation to find how many toppings are on a pizza that costs $27. Example two: Example Three: Complete the table of values: Example four: Make a table of values for each relation: a) y = -2x + 3 Example 5: Homework: b) y= -5x – 4 c) y = 8x -3 6.7 Graphing Linear Equations Example1: Make a table of values for this relation. n 0 1 2 3 p To graph the relation, p = 6n, plot n along the horizontal axis and p along the vertical axis. Label the axes and write the equation of the relation on the graph. The points lie in a straight line, so the relation is linear. Since Sylvia only gets paid for whole numbers of trays planted we do not join the points. These data are discrete. When data is discrete, there are numbers between those given that are not meaningful in the context of the problem. The graph shows that for every tray Sylvia plants, her pay increases by $6. As the number of trays increases, so does her pay. Example two: a) Create a table of values for the relation. g b 0 1 2 3 4 ………… ………… 24 b) Graph the relation. Example three: x -4 -3 -2 -1 0 1 2 3 4 y b) Graph the relation and describe the relation between the variables. y -x x -y Homework: